TD 8-9¶

Filtrage linéaire¶

Exercice 1 : Spectre d’un signal triangulaire - ★¶

On étudie un signal triangulaire de période 1 ms et d’amplitude $0,5 \mathrm{~V}$ . Le développement en série de Fourier de ce signal triangulaire est donné par :

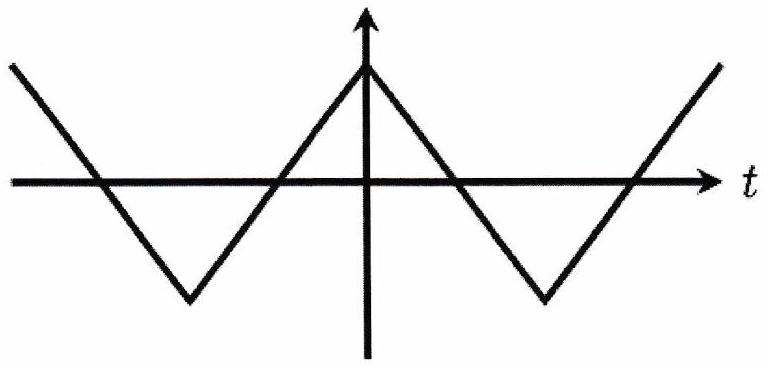
s(t)=\sum_{n=1}^{\infty} \frac{8 A}{((2 n-1) \pi)^{2}} \cos ((2 n-1) \omega t)

(1)

Quelle est la fréquence du signal triangulaire ?
Quelles sont les fréquences et amplitudes des quatre premières harmoniques?
Tracer le spectre.

Exercice 2 : Choix du filtre -¶

Quel filtre choisir pour passer du signal $e(t)$ au signal $s(t)$ ? Indiquer ses caractéristiques.

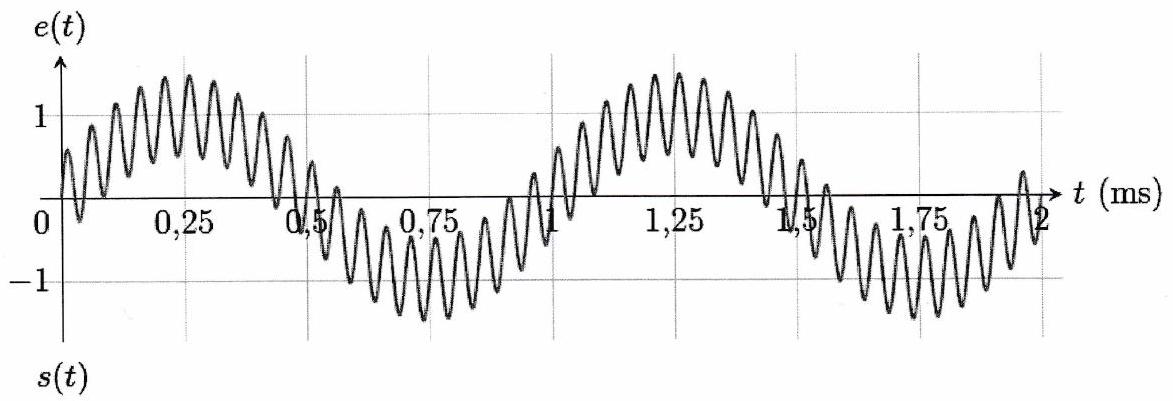
Quel filtre choisir (type et caractéristiques) pour réaliser les opérations suivantes? (a) Supprimer la composante continue d’un signal afin de ne s’intéresser qu’à la partie alternative. (b) Moyenner un signal périodique de fréquence 300 Hz . (c) Éliminer le bruit autour du signal récupéré par un microphone placé devant un diapason.

Exercice 3 : Comportements asymptotiques - ★¶

À partir des comportements asymptotiques, assigner à chaque grandeur ci-dessous le type de filtre correspondant.

Passe-bas
Passe-bande
Passe-haut

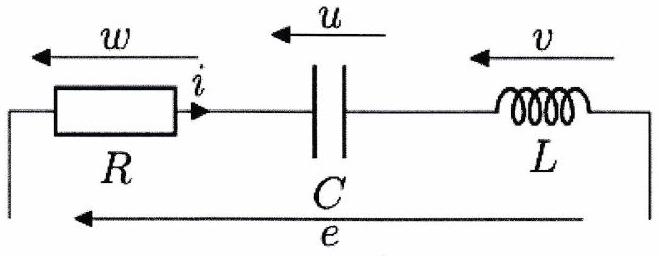
Pour chacun des circuits ci-dessous, déterminer la nature du filtre.

(a)

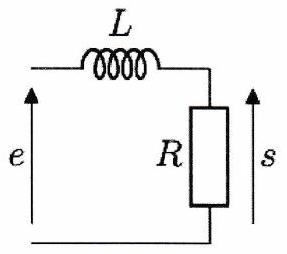
(b)

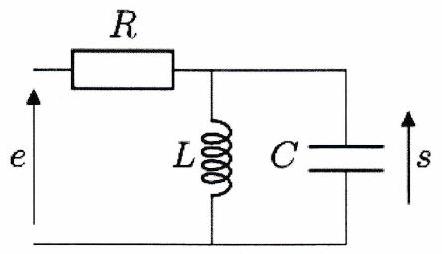
(c)

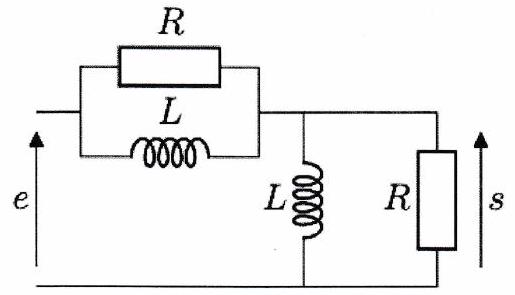
Exercice 4 : Couplage AC et DC de l’entrée d’un oscilloscope - ★¶

La figure ci-contre montre un signal créneau de période $T= 0,40 \mathrm{~s}$ tel qu’on le visualise en utilisant le couplage DC (courbe en noir) ou le couplage AC (courbe en gris) d’un oscilloscope. Le calibre vertical est $1 \mathrm{~V} /$ division dans les deux cas. Lorsque le couplage AC est choisi, le signal passe à travers un filtre du premier ordre.

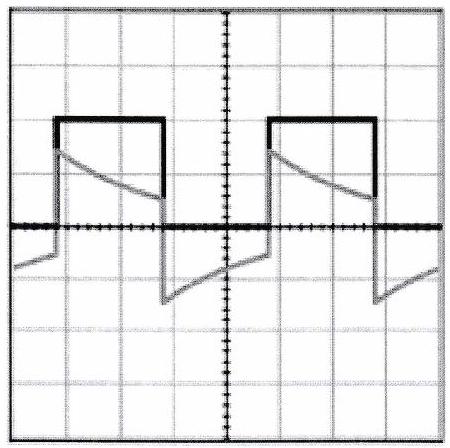
S’agit-il d’un filtre passe-bas ou d’un filtre passe-haut ? Est-ce cohérent avec la fonction du couplage AC ?
Déterminer la limite du gain du filtre lorsque la fréquence tend vers l’infini.
une analyse spectrale montre que l’amplitude du fondamental est égale à $2,5 \mathrm{~V}$ pour le signal non filtré et $2,4 \mathrm{~V}$ pour le signal filtré. En déduire la fréquence de coupure du filtre.

Exercice 5 : Lecture de diagramme de Bode - ★¶

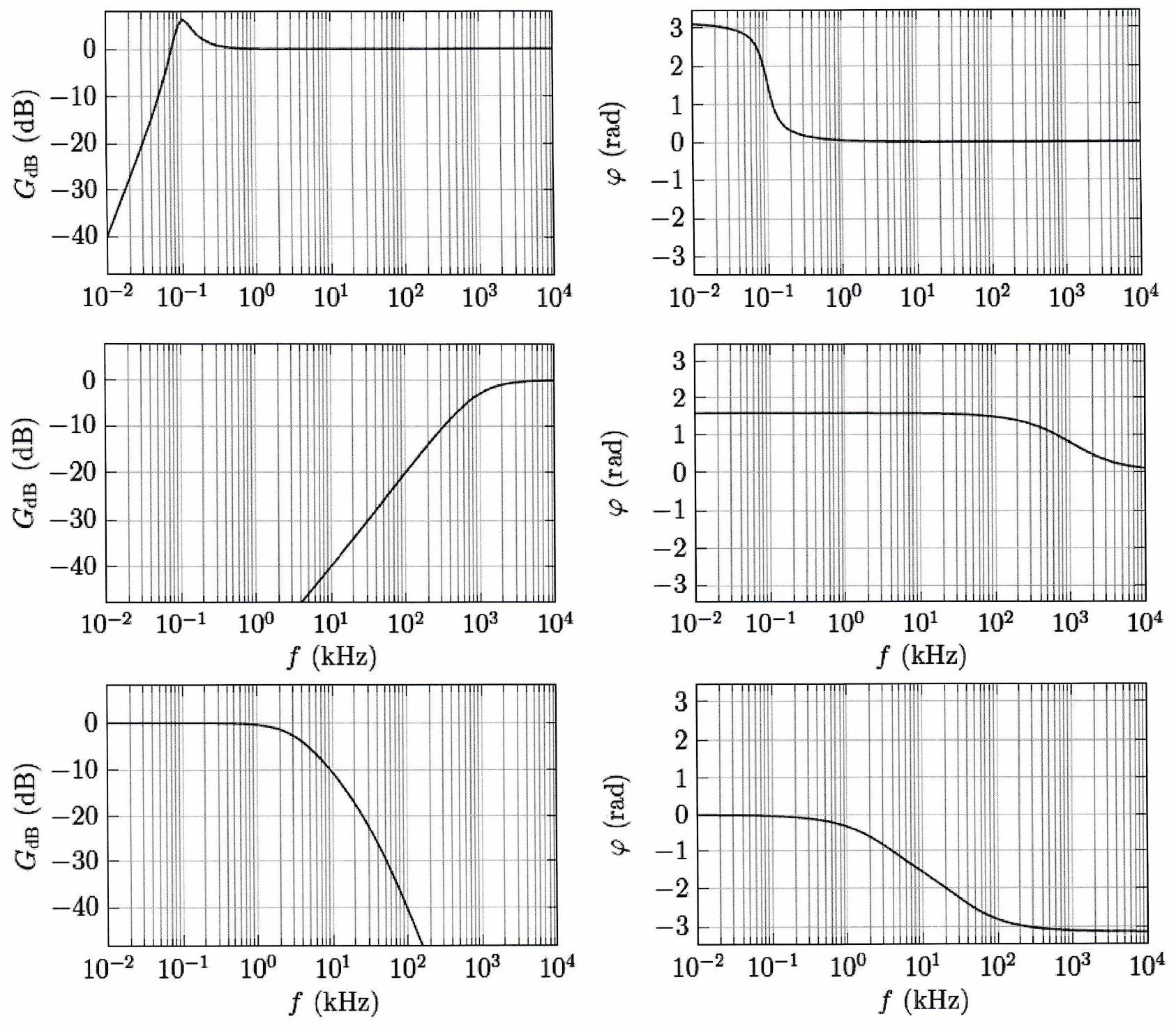
Pour les trois diagrammes de Bode ci-dessous, indiquer le type de filtre dont il s’agit. Préciser s’il peut s’agir d’un filtre d’ordre 1 ou non. Déterminer ensuite, pour chaque filtre, l’expression du signal de sortie $s(t)$ si l’on envoie en entrée le signal $e(t)$ de fréquence $f=1 \mathrm{kHz}$ suivant :

e(t)=E_{0}+E_{0} \cos \left(10 \omega t+\frac{\pi}{4}\right)+E_{0} \cos \left(100 \omega t-\frac{\pi}{3}\right)

(2)

Exercice 6 : Filtre $R L-\star$ ¶

On étudie le filtre ci-contre constitué d’une résistance $R=1,0 \mathrm{k} \Omega$ et d’une bobine idéale d’inductance $L=0,5 \mathrm{H}$ .

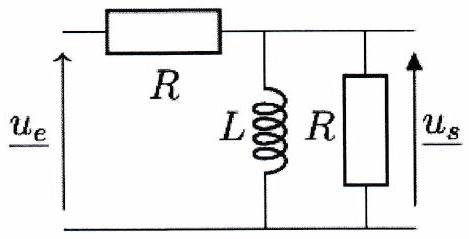
Déterminer la nature du filtre d’après le comportement asymptotique des dipôles.
Établir sa fonction de transfert.
Identifier la ou les affirmations fausses concernant la pulsation de coupure d’un filtre :

c’est la pulsation de l’intersection des deux asymptotes du diagramme de Bode en gain;
c’est la pulsation pour laquelle le gain en décibels vaut le gain en décibels maximal diminué de 3 décibels;
c’est la pulsation pour laquelle le gain vaut la moitié du gain maximal.

Établir l’expression de la pulsation de coupure du filtre. Faire l’application numérique.
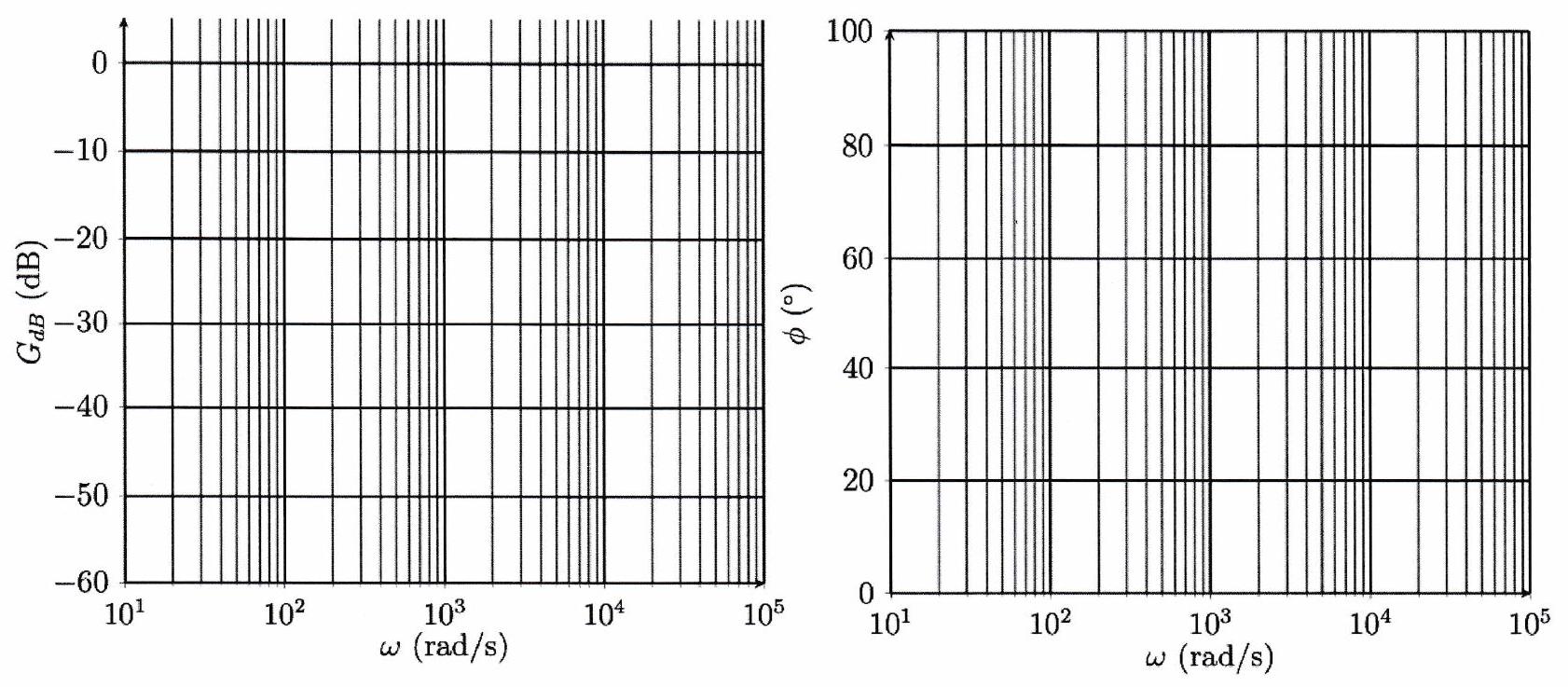
Tracer, après justification, le diagramme de Bode asymptotique sur le papier semi-log fourni ci-dessous.
Tracer le diagramme de Bode réel en ajoutant les points essentiels.

Exercice 7 : Filtrage avant un haut-parleur tweeter¶

Avant d’envoyer le signal en entrée d’un haut-parleur tweeter chargé d’émettre les sons aigus, on place un filtre passe-haut du premier ordre de fréquence de coupure $f_{c}=3500 \mathrm{~Hz}$ . On en donne la fonction de transfert :

\underline{H}(j \omega)=\frac{j \frac{f}{f_{c}}}{1+j \frac{f}{f_{c}}}

(3)

et son diagramme de Bode :

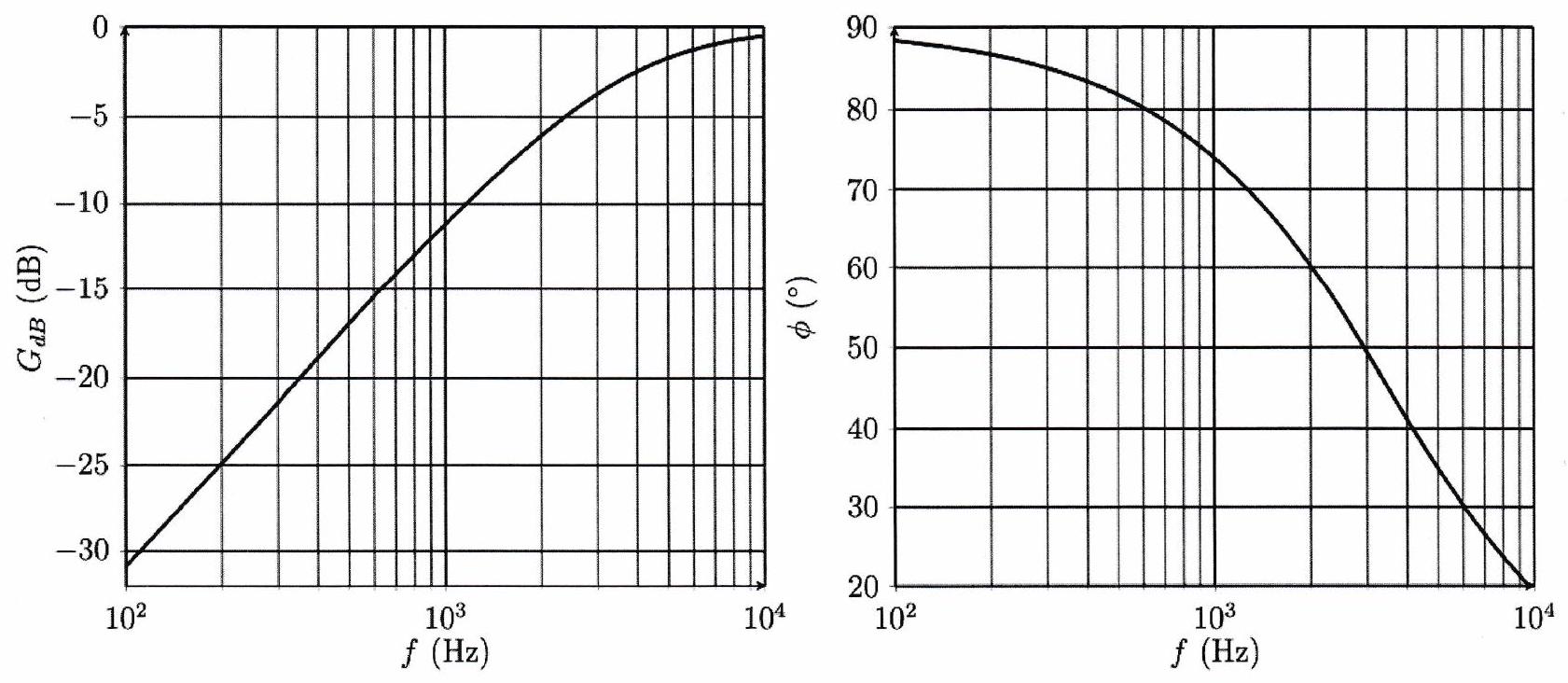
On modélise le son que l’on souhaite transmettre par la somme de trois signaux sinusoïdaux (le spectre de la musique est bien plus complexe, ce qui en donne toute sa beauté, mais l’objectif est de comprendre l’idée...) :

e(t)=E_{0} \cos \left(2 \pi f_{1} t\right)+E_{0} \cos \left(2 \pi f_{2} t+\frac{\pi}{4}\right)+E_{0} \cos \left(2 \pi f_{3} t-\frac{\pi}{5}\right)

(4)

avec $f_{1}=587 \mathrm{~Hz}$ (do du milieu du piano); $f_{2}=2093 \mathrm{~Hz}$ (do7) et $f_{3}=4186 \mathrm{~Hz}$ (do8 dernière touche du piano).

Représenter le spectre en amplitude de $e(t)$ .
Proposer une écriture générale du signal en sortie du filtre et qui sera envoyée en entrée du haut-parleur.
Déterminer toutes les caractéristiques du signal de sortie.
En utilisant une autre couleur, superposer sur le spectre de Q1 le spectre en amplitude de $s(t)$ .

Exercice 8 : Filtre de Wien - ★★¶

On s’intéresse au filtre de Wien représenté cidessous, où $R=1 \mathrm{k} \Omega$ et $C=500 \mathrm{nF}$ .

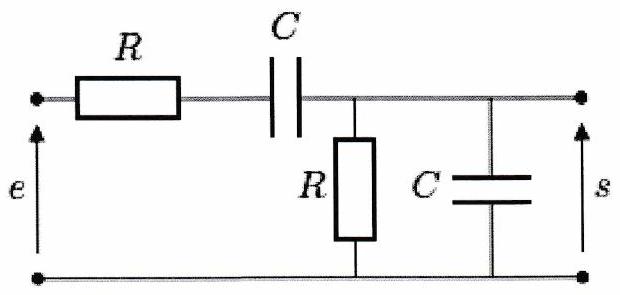
Par analyse des comportements asymptotiques des dipôles, déterminer le type de filtre dont il s’agit.
Montrer que la fonction de transfert s’écrit

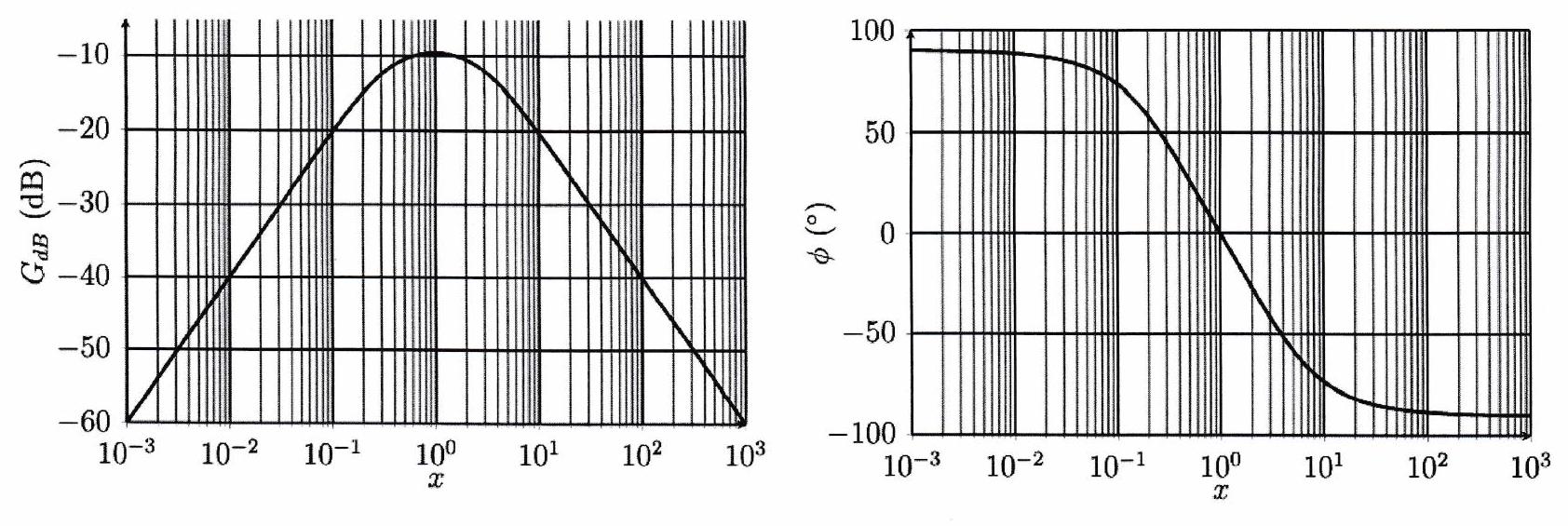
\underline{H}(j \omega)=\frac{H_{0}}{1+j Q\left(\frac{\omega}{\omega_{0}}-\frac{\omega_{0}}{\omega}\right)}

(5)

Donner les expressions de $H_{0}, Q$ et $\omega_{0}$ . 3. Exprimer le gain linéaire, le gain en dB et le déphasage de la tension de sortie par rapport à celle d’entrée, en fonction de $x=\frac{\omega}{\omega_{0}}$ . 4. Calculer simplement le gain maximal $G_{0}$ du filtre, exprimer sa valeur $G_{0, \mathrm{~dB}}$ en dB , et calculer le déphasage $\varphi_{0}$ correspondant. 5. Déterminer les fréquences de coupure et en déduire la bande passante du circuit. 6. Le diagramme de Bode de ce filtre est représenté ci-dessous. Expliquer les valeurs prises par la pente en haute et basse fréquence. 7. Déterminer l’expression du signal de sortie pour un signal d’entrée de la forme :

e(t)=E_{0}+E_{0} \cos (\omega t)+E_{0} \cos (10 \omega t)+E_{0} \cos (100 \omega t) \quad \text { où } \omega=200 \mathrm{rad} \cdot \mathrm{~s}^{-1}

(6)

Exercice 9 : Filtres $R L C$ série - ★★¶

On étudie les deux circuits linéaires représentés ci-dessous, dont l’expression des fonctions de transfert est donnée.

\underline{H}_{1}(j \omega)=\frac{1}{1-\left(\frac{\omega}{\omega_{0}}\right)^{2}+j \frac{\omega}{Q \omega_{0}}}

(7)

\underline{H}_{2}(j \omega)=\frac{j Q \frac{\omega}{\omega_{0}}}{1+j Q\left(\frac{\omega}{\omega_{0}}-\frac{\omega_{0}}{\omega}\right)}

(8)

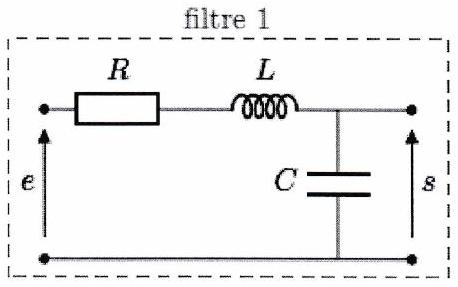
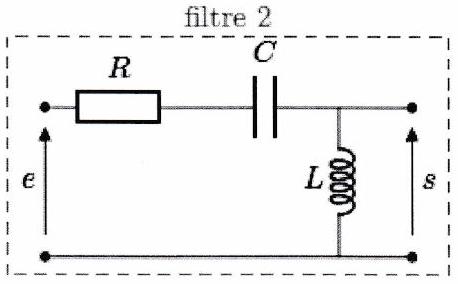
On pourra traiter les questions pour le filtre 1, puis pour le filtre 2.

Par analyse des comportements asymptotiques du circuit, déterminer le type de filtre dont il s’agit.
Retrouver l’expression de la fonction de transfert et donner les expressions de $\omega_{0}$ et $Q$ . Donner l’ordre du filtre.
Donner l’expression de l’équation différentielle reliant $s(t)$ et $e(t)$ .
Exprimer le gain et la phase du filtre en fonction de $\omega, \omega_{0}$ et $Q$ .

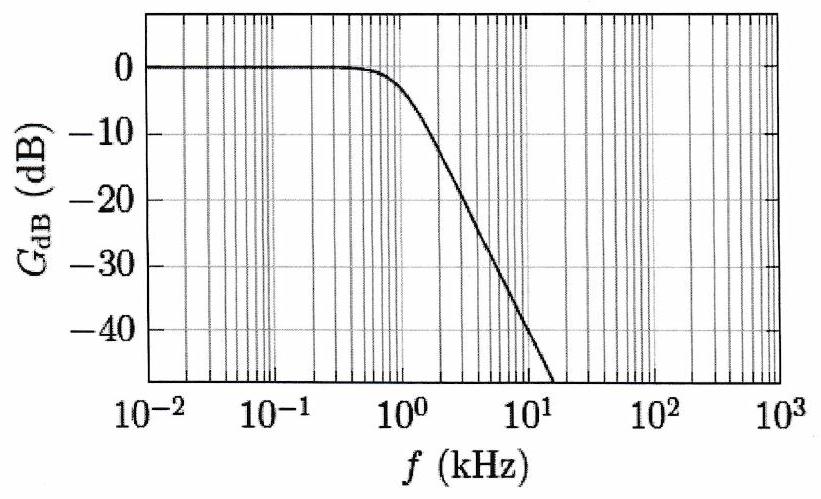
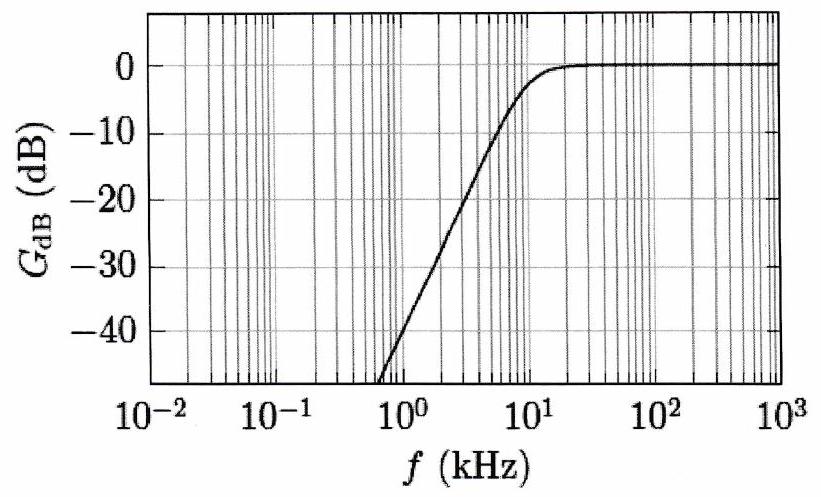
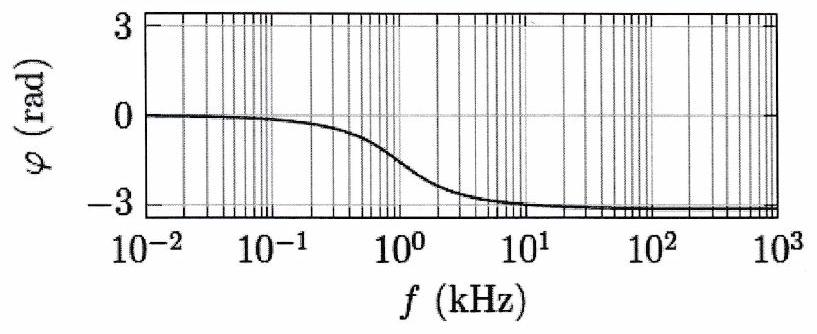
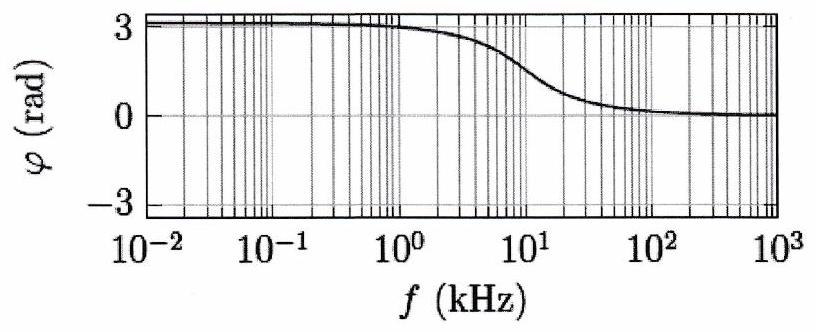
Les diagrammes de Bode de ces filtres sont représentés ci-dessous pour $Q=\frac{1}{\sqrt{2}}$ . 5. Retrouver les pentes des asymptotes à basse fréquence et à $\mathrm{g}=$ haute fréquence. 6. Commenter l’intérêt d’utiliser un tel filtre plutôt qu’un filtre du même type mais d’ordre 1 en comparant leur action sur un signal d’entrée de pulsation $\omega_{e}=2 \pi \times 1 \mathrm{kHz}$ de la forme $e(t)=E_{0} \cos \left(\omega_{e} t\right)+E_{0} \cos \left(10 \omega_{e} t\right)$ .

Exercice 10 : Impédance d’entrée d’un oscilloscope - ★★¶

On considère le filtre représenté ci-contre.

Établir l’expression de la fonction de transfert $\underline{H}(j \omega)=\frac{\underline{s}}{\underline{e}}$ où l’on posera $\omega_{0}=\frac{1}{R C}$

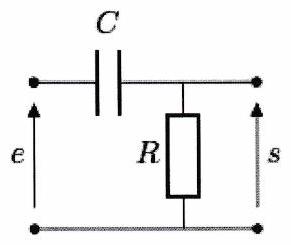
Représenter son diagramme de Bode.
Déterminer la fréquence de coupure pour $R=500 \mathrm{k} \Omega$ et $C=0,1 \mathrm{nF}$ .

On mesure la tension de sortie à l’aide d’un oscilloscope dont l’entrée peut être assimilée à une association en parallèle d’une capacité $C_{0}=30 \mathrm{pF}$ et d’une résistance $R_{0}=1 \mathrm{M} \Omega$ .

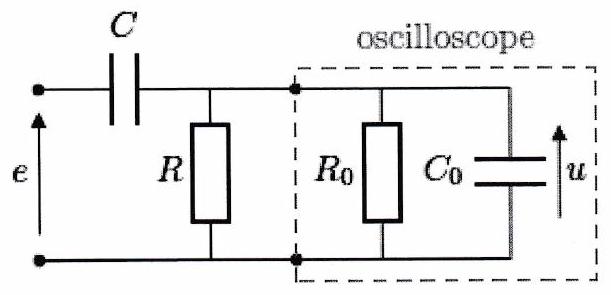
Montrer que la nouvelle fonction de transfert s’exprime :

\underline{H}(j \omega)=\frac{\underline{u}}{\underline{e}}=H_{0} \frac{j R_{\text {éq }}\left(C+C_{0}\right) \omega}{1+j R_{\text {éq }}\left(C+C_{0}\right) \omega} \quad \text { avec } \quad H_{0}=\frac{C}{C+C_{0}} \quad \text { et } \quad R_{\text {éq }}=\frac{R R_{0}}{R+R_{0}}

(9)

et déterminer la nouvelle fréquence de coupure. Conclure sur l’influence de l’oscilloscope. 10. Comment choisir les valeurs des composants $R$ et $C$ pour que l’influence de l’oscilloscope soit négligeable?

Exercice 11 : Conception d’un filtre de signaux acoustiques $-\star \star$ ¶

Un dispositif de traitement de signaux acoustiques nécessite la séparation des composantes sonores et ultrasonores. On souhaite éliminer les composantes ultrasonores : il faut donc réaliser un filtre passe-bas. Le cahier des charges du dispositif indique les caractéristiques suivantes:

fréquence de coupure 20 kHz ;
gain nominal (gain en basse fréquence) 0 dB ;
l’atténuation des fréquences comprises entre 0 et 20 kHz doit être inférieure à 3 dB ;
l’atténuation des fréquences supérieures à 40 kHz doit être supérieure à 10 dB .

Le filtre le plus simple serait un passe-bas du premier ordre de fréquence de coupure $f_{c}=20 \mathrm{kHz}$ . On rappelle que la fonction de transfert d’un tel filtre s’écrit sous forme réduite est :

\underline{H_{1}}(j \omega)=\frac{1}{1+j \omega / \omega_{c}} \quad \text { avec } \quad \omega_{c}=2\pi f_{c}

(10)

Retrouver la pente des asymptotes du diagramme de Bode en gain de ce filtre et calculer son gain à la fréquence de coupure.
Montrer qu’il ne peut satisfaire au cahier des charges imposé. Justifier qu’il est nécessaire d’utiliser un filtre d’ordre plus élevé.

On se tourne alors vers un filtre passe-bas du second ordre de fonction de transfert :

\underline{H_{2}}(j \omega)=\frac{1}{1-\left(\frac{\omega}{\omega_{0}}\right)^{2}+j \frac{\omega}{Q \omega_{0}}}

(11)

Retrouver la pente des asymptotes du diagramme de Bode en gain de ce filtre. Peut-il satisfaire au cahier des charges imposé ?
Calculer le gain en décibel de ce filtre pour $f=f_{c}$ . En déduire les valeurs de $Q$ permettant de satisfaire au cahier des charges.

Exercice 12 : Dimensionnement d’un moyenneur - ★★¶

Le signal ci-dessous est délivré par un capteur. La grandeur que vous cherchez à mesurer est directement reliée à la valeur moyenne du signal.

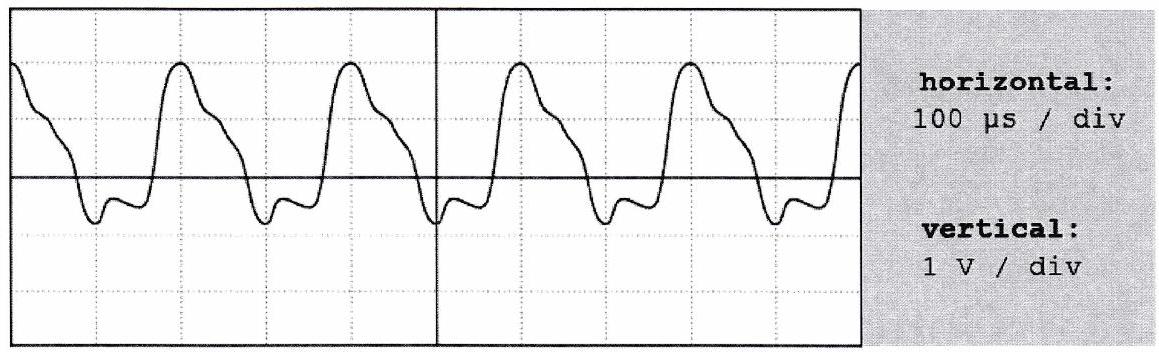
Où se trouve la valeur moyenne d’un signal dans son spectre en amplitude ?
En déduire duquel de ces filtres vous avez besoin.

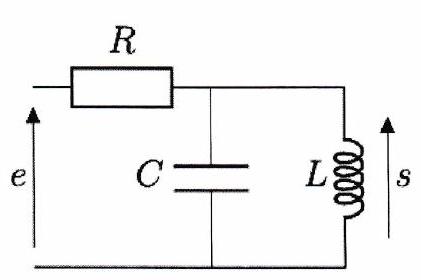
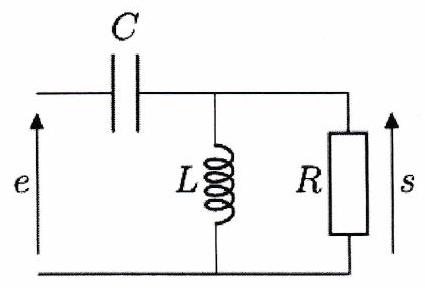
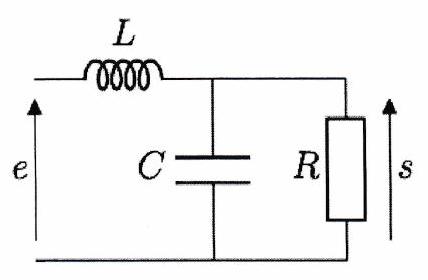
Exprimer la fonction de transfert et la mettre sous la forme :

\underline{H}(j \omega)=\frac{1}{1-\left(\frac{\omega}{\omega_{0}}\right)^{2}+j \frac{\omega}{Q \omega_{0}}} \quad \text { avec } \omega_{0}=\frac{1}{\sqrt{L C}}

(12)

Donner l’expression du facteur de qualité $Q$ en fonction de $R, L$ et $C$ . 4. Tracer le diagramme de Bode en amplitude et y faire explicitement apparaître $\omega_{0}$ . Quel rôle joue cette grandeur ? 5. Cherchez-vous à produire un phénomène de résonance ou bien à l’éviter ? En déduire parmi les jeux proposés ci-dessous le plus adapté pour ...

TD 8-9