Ondes stationnaires¶

Exercice 1 : Frettes d’une guitare - ★¶

Les frettes placées le long du manche d’une guitare permettent au musicien de modifier la hauteur du son produit par la corde. En pressant la corde contre une frette, il diminue sa longueur, provoquant une augmentation de la fréquence fondamentale de vibration de la corde.

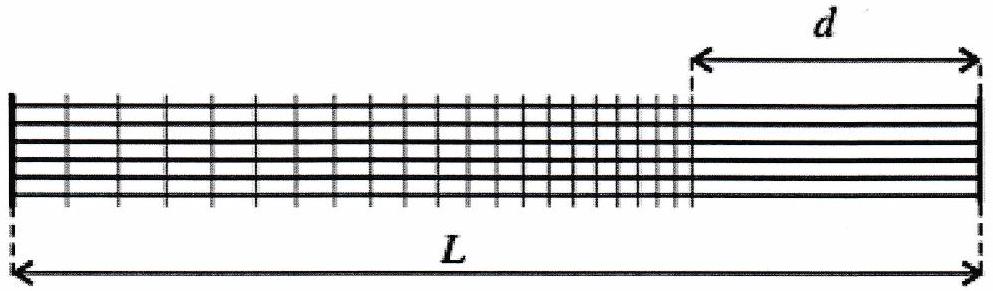
Retrouver rapidement la fréquence de vibration fondamentale d’une corde de longueur $L$ , attachée à ses deux extrémités, le long de laquelle les ondes se propagent à la célérité $c$ .
La note monte d’un demi-ton lorsque la fréquence est multipliée par $2^{1 / 12}$ . Pour cela, comment doit-on modifier la longueur de la corde ?
En plaçant le doigt sur les frettes successives, on monte à chaque fois la note d’un demiton. Combien de frettes peut-il y avoir au maximum, sachant que la distance $d$ entre la dernière frette et le point d’accrochage de la corde (voir figure) doit être supérieur à $0,25 L$ ?

Exercice 2 : Modélisation d’instruments à vent - ★¶

On modélise simplement les instruments dans cet exercice : une colonne d’air rectiligne, de longueur $L$ , ouverte ou fermée à ses extrémités. On notera $p(x, t)=P(x, t)-P_{a}$ la surpression acoustique ( $P_{a}$ est la pression atmosphérique, et $P(x, t)$ la pression totale en $x$ à l’instant $t$ ). On distingue, pour chaque extrémité de position $x_{e}$ , les deux types de conditions aux limites suivants :

Premier cas de figure : l’extrémité du tuyau est ouverte. On a alors $p\left(x_{e}, t\right)=0$ , la surpression est nulle (car la pression qui y est imposée est la pression atmosphérique).
Deuxième cas de figure : le tuyau est fermé à cette extrémité, et donc $p\left(x_{e}, t\right)$ est d’amplitude maximale (en raison de la réflexion). On modélise alors différents instruments, dont les deux extrémités sont ouvertes ou fermées. Dans tout l’exercice, on considère que la célérité du son dans l’air est $c_{s}=340 \mathrm{~m} \cdot \mathrm{~s}^{-1}$ .

L’orgue : Le tuyau d’orgue est ouvert à ses deux extrémités. Représenter les trois premiers modes de $p(x, t)$ dans le tuyau, puis déterminer la fréquence des modes propres. Calculer la longueur minimale du tuyau pour qu’il puisse produire un Do 0 de fréquence $f=34 \mathrm{~Hz}$ .
La clarinette : Le tuyau est fermé au niveau de l’embouchure (là où on souffle), et ouvert à l’autre extrémité. Représenter les trois premiers modes de $p(x, t)$ , puis déterminer les fréquences des modes propres de la clarinette. Quelle propriété remarquable présentent les harmoniques de la clarinette ?
Clé de douzième de la clarinette : La clarinette est munie d’un système qui peut ouvrir un trou en $x=L / 3$ , et la surpression en ce point est donc nulle. Calculer les nouveaux modes propres de la clarinette, et expliquer quel est l’effet de l’ouverture du trou sur le son émis par l’instrument.

Exercice 3 : Tube à ondes stationnaires - ★¶

Un haut-parleur est placé à l’entrée d’un tube à ondes stationnaires. Il est alimenté par une tension sinusoïdale de pulsation $\omega$ . La célérité des ondes sonores est notée $c$ .

Quelle est la grandeur physique qui oscille ?
Donner la forme de l’onde $p_{i}(z, t)$ engendrée par le haut-parleur.
Une surface réfléchissante placée en bout de tube (repérée par $z=0$ ) engendre une onde réfléchie. Donner la forme générale de cette onde réfléchie $p_{r}(z, t)$ sans expliciter les différentes inconnues pour l’instant.
La surface réfléchissante en $z=0$ est telle qu’elle correspond à un ventre de vibration. Expliciter les différentes inconnues dans la forme de l’onde réfléchie grâce à cette condition aux limites.
En déduire la forme de l’onde totale $p(z, t)$ . Montrer que cela correspond effectivement à une onde stationnaire. Représenter-la à différents instants.
Proposer une méthode pour mesurer la longueur d’onde.

Exercice 4 : Accordage d’un piano - ★★¶

Un piano est constitué d’un grand nombre de cordes tendues, mises en vibration par un marteau qui les frappe lorsque la touche correspondante est abaissée. L’objectif de l’exercice est de déterminer quels facteurs physiques influencent le son produit par la corde, de découvrir une technique pour accorder le piano, et les effets d’anharmonicité dus à la raideur des cordes.

Célérité des ondes : On suppose que la célérité $c$ des ondes se propageant sur la corde dépend de trois paramètres : la masse volumique $\rho$ de la corde, son diamètre $d$ et la force $T$ de tension appliquée à la corde. Par analyse dimensionnelle, déterminer $c$ à un préfacteur numérique $k$ près. On remarquera notamment que $c \propto \sqrt{T}$ .
Accordage d’un piano: On suppose que la fréquence fondamentale de vibration de la corde est proportionnelle à $T^{\alpha}$ . (a) Déterminer la valeur de l’exposant $\alpha$ par analyse dimensionnelle. (b) Pour accorder le piano, on joue une même note sur un deuxième piano, dont on sait qu’il est bien accordé. Qu’entend-on lorsque la note est jouée simultanément sur les deux pianos? (c) On suppose que l’oreille humaine est capable d’entendre les battements s’ils ont une période comprise entre $0,5 \mathrm{~s}$ et 5 s . Avec quelle précision relative peut-on accorder les pianos (c’est-à-dire obtenir que les deux cordes vibrent à la même fréquence fondamentale) ?
Anharmonicité de la corde : En fait, il faut aussi tenir compte de la raideur de la corde. La relation de dispersion pour une onde sur la corde de piano s’écrit

\omega=c k \sqrt{1+\beta k^{2}}

(1)

avec $k$ la norme du vecteur d’onde et $\beta$ une constante qui dépend de la raideur de la corde. (a) Déterminer la dimension de $\beta$ . (b) Quelles sont les valeurs possibles de $k$ pour une onde stationnaire sur cette corde ? En déduire les fréquences des modes propres. Comparer avec le cas “idéal” où $\beta=0$ . (c) Expliquer pourquoi un piano de concert, dont les cordes sont plus longues qu’un piano d’étude, produit un son de meilleure qualité.

Exercice 5 : Étude énergétique - ★★★¶

On considère une corde de masse linéique $\mu$ (c’est-à-dire la masse par unité de longueur de corde), on note $u(x, t)$ l’altitude de la corde en $x$ à l’instant $t$ . La corde est fixée en $x=0$ et en $x=L$ . On considère le mode propre $n$ qui s’exprime de la façon suivante :

u(x, t)=u_{0} \sin \left(\frac{n \pi x}{L}\right) \sin \left(\frac{n \pi c t}{L}\right)

(2)

où $u_{0}$ est l’amplitude du mode et $c$ la célérité des ondes.

On note $\mathrm{d} \mathcal{E}_{c}$ l’énergie cinétique de la portion de corde comprise entre $x$ et $x+\mathrm{d} x(\mathrm{~d} x$ étant une longueur infiniment faible). Donner l’expression de $\mathrm{d} \mathcal{E}_{c}$ .
En déduire l’énergie cinétique totale de la corde.
Une étude approfondie montrerait que l’énergie potentielle de la portion de corde comprise entre $x$ et $x+\mathrm{d} x$ est de la forme

\mathrm{d} \mathcal{E}_{p}=\frac{1}{2} \alpha\left(\frac{\mathrm{~d} u_{t}(x)}{\mathrm{d} x}\right)^{2} \mathrm{~d} x

(3)

On dérive ici la fonction uniquement par rapport à $x$ et on pourra donc considérer que $t$ est une constante. $\alpha$ est une constante, montrer qu’elle a la dimension d’une force. 4. En déduire l’énergie potentielle totale de la corde. 5. En utilisant la conservation de l’énergie de la corde, exprimer $\alpha$ en fonction de la vitesse de propagation et de la masse linéique. 6. Exprimer l’énergie mécanique totale de la corde, comment dépend-t-elle du mode considéré ? 7. Calculer $\mathrm{d} \mathcal{E}_{m}$ l’énergie mécanique d’une portion de corde de longueur $\mathrm{d} x$ , pourquoi cette énergie dépend du temps contrairement à celle de la corde ?