Phénomènes d’interférences¶

Les phénomènes d’interférences apparaissent quand deux ondes (ou plus) de même fréquence se superposent dans une zone de l’espace. Le déphasage des ondes étant différent en chaque point $M$ , l’amplitude de l’onde résultant de la superposition dépend de $M$ .

Exemple¶

Brouillage, interférences radio, couleurs interférentielles (irisation : bulles de savon, tache d’huile, couleur des papillons, de certaines plumes, etc.). Par ailleurs, de nombreux instruments exploitent des interférences lumineuses pour des applications très variées : mesures de surfaces, interféromètres gravitationnels, etc.

I) Superposition des deux signaux sinusoïdaux de même fréquence¶

Dans ce paragraphe, on s’intéresse au signal obtenu en faisant la somme de deux signaux sinusoïdaux de même fréquence $f$ , donc de même pulsation $\omega=2 \pi f$ .

A) Mise en évidence¶

Expérience 1 : Expérimentation mathématique¶

À l’aide d’une calculatrice graphique, visualiser le signal $s(t)$ , somme des signaux $s_{1}(t)= 4 \cos (2 \pi t)$ et $s_{2}(t)=3 \cos (2 \pi t+\varphi)$ de même fréquence $f=1 \mathrm{~Hz}$ , pour différentes valeurs de $\varphi$ . Qu’observez-vous? $\_\_\_\_$ $\_\_\_\_$ $\_\_\_\_$ $\_\_\_\_$ Tracer les courbes obtenues pour des valeurs bien choisies de $\varphi$ . $\_\_\_\_$ $\_\_\_\_$ $\_\_\_\_$ $\_\_\_\_$ $\_\_\_\_$ $\_\_\_\_$ $\_\_\_\_$ $\_\_\_\_$ On change le deuxième signal en $s_{2}(t)=4 \cos (2 \pi t+\varphi)$ , signal de même amplitude que $s_{1}(t)$ . Qu’observez-vous alors ? $\_\_\_\_$ $\_\_\_\_$

B ) Amplitude de la somme de deux signaux sinusoïdaux¶

1 ) Cas où les deux signaux ont la même amplitude¶

Exercice de cours à connaître 1¶

Soit deux signaux sinusoïdaux $s_{1}(t)=A_{0} \cos \left(\omega t+\varphi_{1}\right)$ et $s_{2}(t)=A_{0} \cos \left(\omega t+\varphi_{2}\right)$ de même pulsation (donc même fréquence) et de même amplitude $A_{0}$ .

En utilisant les formules de trigonométrie, donner l’expression du signal $s(t)$ .
Quelle est son amplitude ?

2 ) Cas où les deux signaux ont des amplitudes différentes

Exercice de cours à connaître 2¶

Soit deux signaux sinusoïdaux $s_{1}(t)=A_{1} \cos \left(\omega t+\varphi_{1}\right)$ et $s_{2}(t)=A_{2} \cos \left(\omega t+\varphi_{2}\right)$ de même pulsation (donc même fréquence).

En utilisant les formules de trigonométrie, donner l’expression du signal $s(t)$ .
Quelle est son amplitude ?

Formule des interférences¶

Le signal résultant de la superposition de deux signaux sinusoïdaux de même fréquence, d’amplitudes $A_{1}$ et $A_{2}$ et de phases initiales $\varphi_{1}$ et $\varphi_{2}$ est un signal sinusoïdal de même fréquence et d’amplitude donnée par la formule des interférences:

A=\sqrt{A_{1}^{2}+A_{2}^{2}+2 A_{1} A_{2} \cos \left(\varphi_{1}-\varphi_{2}\right)}

(1)

Cette amplitude n’est pas égale à la somme des amplitudes des deux signaux.

Remarque¶

Dans le cas où $A_{1}=A_{2}=A_{0}$ , la formule des interférences devient:

A=2 A_{0} \sqrt{\frac{1+\cos \left(\varphi_{1}-\varphi_{2}\right)}{2}}=2 A_{0}\left|\cos \left(\frac{\varphi_{1}-\varphi_{2}}{2}\right)\right|

(2)

qui n’est autre que la formule trouvée dans la première partie.

C ) Influence du déphasage¶

L’amplitude $A$ de l’onde résultante dépend du déphasage entre les deux signaux :

\Delta \varphi=\varphi_{1}-\varphi_{2}

(3)

Remarque¶

$\Delta \varphi$ défini ci-dessus est le déphasage du signal $s_{1}$ par rapport au signal $s_{2}$ . On aurait pu aussi choisir le déphasage de $s_{2}$ par rapport à $s_{1}$ , qui est l’opposé.

1 ) Interférences constructives¶

L’amplitude résultante $A$ est maximale lorsque :

\cos (\Delta \varphi)=\cos \left(\varphi_{1}-\varphi_{2}\right)=1

(4)

On parle alors d’interférences constructives. C’est le cas si :

\Delta \varphi=2 m \times \pi \text { avec } m \in \mathbb{Z}

(5)

c’est-à-dire si les deux signaux sont en phase. La valeur maximale de $A$ est :

A_{\max }=\sqrt{A_{1}^{2}+A_{2}^{2}+2 A_{1} A_{2}}=\sqrt{\left(A_{1}+A_{2}\right)^{2}} \text { soit } A_{\max }=A_{1}+A_{2}

(6)

2 ) Interférences destructives¶

L’amplitude résultante $A$ est minimale lorsque :

\cos (\Delta \varphi)=\cos \left(\varphi_{1}-\varphi_{2}\right)=-1

(7)

On parle alors d’interférences destructives. C’est le cas si :

\Delta \varphi=(2 m+1) \times \pi \text { avec } m \in \mathbb{Z}

(8)

c’est-à-dire si les deux signaux sont en opposition de phase. La valeur minimale de $A$ est :

A_{\min }=\sqrt{A_{1}^{2}+A_{2}^{2}-2 A_{1} A_{2}}=\sqrt{\left(A_{1}-A_{2}\right)^{2}} \text { soit } A_{\min }=\left|A_{1}-A_{2}\right|

(9)

II ) Interférences entre deux ondes acoustiques ou mécaniques de même fréquence¶

A) Phénomène d’interférences¶

Lorsque deux ondes de même nature, sinusoïdales et de même fréquence se propagent dans une zone de l’espace, elles s’additionnent en tout point. L’amplitude résultante dépend, comme on vient de le voir, du déphasage entre les deux ondes. Or, ce déphasage varie d’un point à l’autre de l’espace. L’onde résultante a alors une amplitude modulée dans l’espace. C’est le phénomène d’interférences.

Dans le cas d’ondes acoustiques ou mécaniques, on sait mesurer l’amplitude en différents points de l’espace.

B) Observation expérimentale¶

Simulation 1 : Cuve à ondes¶

Première animation : https://phyanim.sciences.univ-nantes.fr/Ondes/cuve_ ondes/propagation_onde_circulaire.php

Une pointe attachée à un vibreur frappe la surface de l’eau et crée une onde circulaire qui progresse à la surface. Un système optique permet de visualiser la surface. On néglige toutes les sources d’atténuation de l’onde. On représente l’évolution temporelle du déplacement vertical (“élongation”) $s\left(x_{0}, t\right)$ avec $x_{0}$ un point fixe à la surface de l’eau.

À quoi correspondent les zones claires et sombres? Minimum
Quelle est la distance entre traits brillants (ou sombres) consécutifs?

Une eongsur d’ onde 3. Quelle expression peut-on donner à

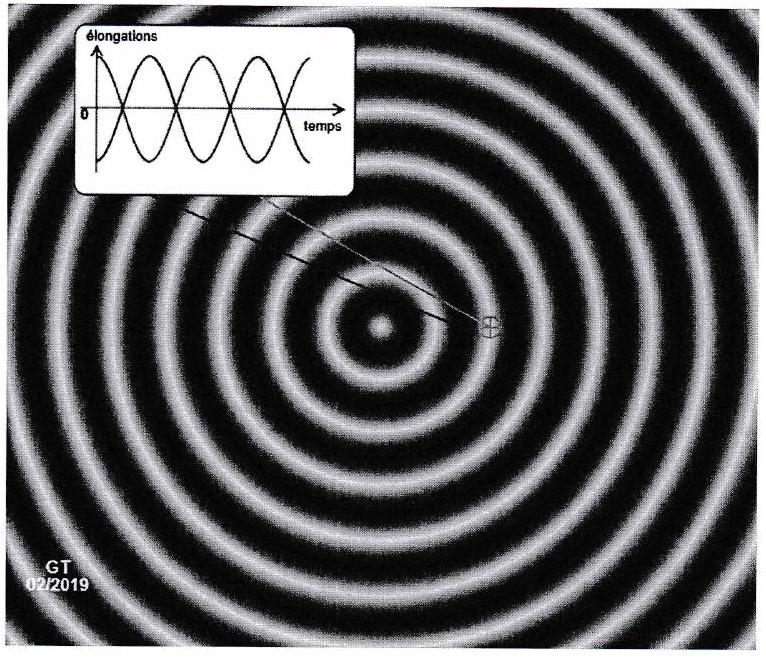
$s(x, t)$ ? Comment peut-on qualifier une telle onde? Onde progressive simutoídal $x>0: s(x, t)=s_{0} \cos \left(\omega t-k x+\varphi_{0}\right) \quad x<0: \delta(x, t)=s_{0}$ col $\left(\omega t+k x+\varphi_{0}\right)$ Deuxième animation : https://phyanim.sciences.univ-nantes.fr/Ondes/cuve_ ondes/interference_ondes_circulaires.php

On introduit un autre vibreur, créant ainsi deux sources de vibrations sinusoïdales $S_{1}$ et $S_{2}$ vibrant à la même fréquence, avec la même amplitude et de même phase à l’origine. On observe alors l’onde résultant de la superposition de ces deux ondes.

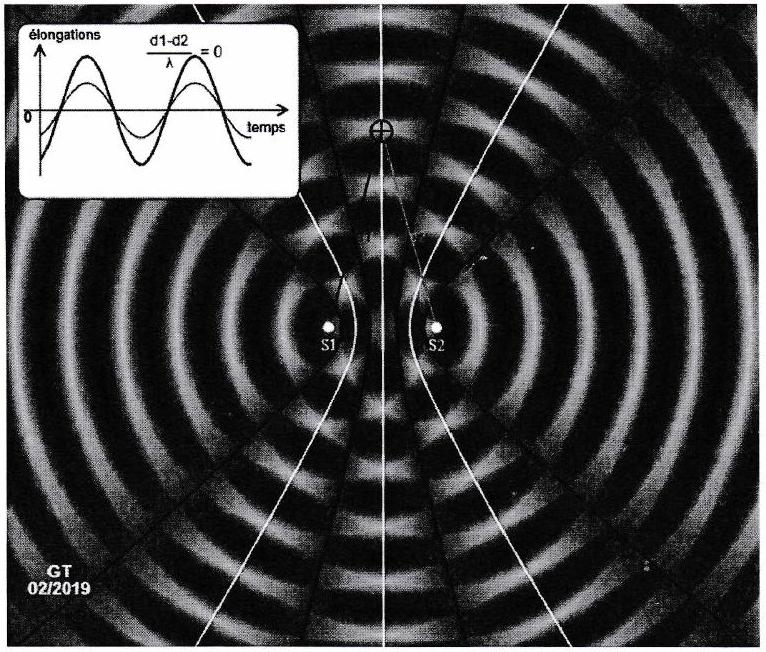
À la surface de l’eau, on observe des zones (lignes claires) où l’amplitude de l’onde résultante est maximale, les deux ondes issues de $S_{1}$ et $S_{2}$ sont en phase en tout point de cette ligne brillante.

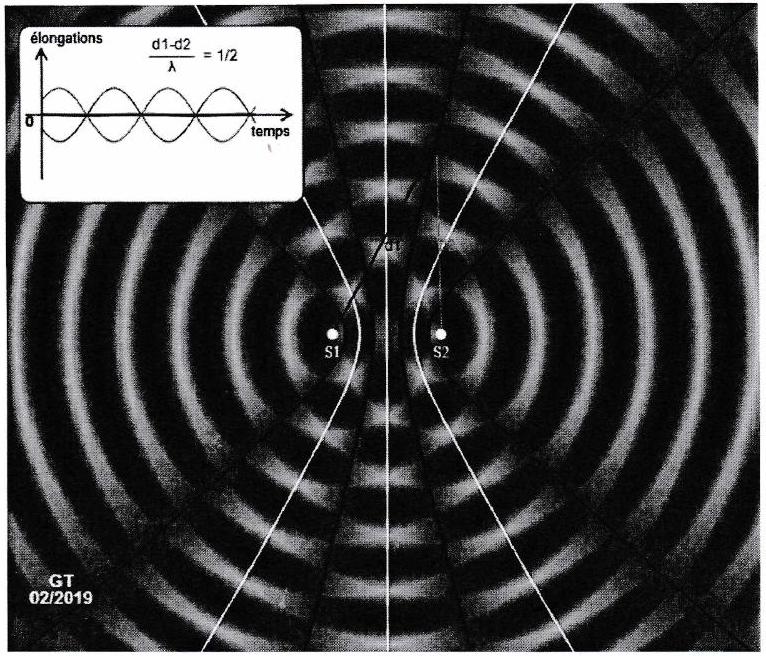
À la surface de l’eau, on observe également des zones (lignes sombres) où l’amplitude de l’onde résultante est faible, voire quasi nulle. Les ondes issues de $S_{1}$ et $S_{2}$ sont en opposition de phase en tout point de cette ligne sombre.

Ces lignes claires sont appelées “franges brillantes”.

Ces lignes sombres sont appelées “franges sombres”.

Les autres points de l’espace situés entre les franges sombres et les franges brillantes vibrent avec une amplitude qui varie de zéro à l’amplitude maximale. On dit que l’amplitude est modulée spatialement.

C ) Étude théorique¶

Exercice de cours à connaître 3¶

Donner l’expression de $s_{1}\left(S_{1}, t\right)$ et de $s_{2}\left(S_{2}, t\right)$ les deux ondes issues de $S_{1}$ et $S_{2}$ .
En déduire l’expression de $s_{1}(M, t)$ et $s_{2}(M, t)$ au point $M$ auquel l’onde résultante est observée. On donnera l’expression en fonction notamment de $d_{1}, d_{2}$ et $\lambda$ la longueur d’onde.
Donner alors le déphasage de entre les deux ondes au point $M$ .
En déduire l’expression de l’amplitude de l’onde résultante au point $M$ .
Donner une condition sur $d_{1}$ et $d_{2}$ pour que avoir, au point $M$ , des interférences constructives. Faire de même pour des interférences destructives.

D) Bilan¶

Phénomène d’interférence¶

L’amplitude de l’onde $s(M, t)$ résultant de la superposition de deux ondes synchrones (de même fréquence) issues de $S_{1}$ et $S_{2}$ , de longueur d’onde $\lambda$ , dépend du déphasage $\Delta \varphi(M)$ entre les deux ondes incidentes en $M$ :

\Delta \varphi=\frac{2 \pi}{\lambda}\left(S_{2} M-S_{1} M\right)=k\left(S_{2} M-S_{1} M\right)

(10)

L’amplitude de l’onde $s(M, t)$ est donc maximale (resp. minimale) si $\Delta \varphi \equiv 0[2 \pi]$ (resp. $\Delta \varphi \equiv \pi[2 \pi]$ ). En $M$ , les ondes issues de $S_{1}$ et $S_{2}$ sont alors en phase (resp. opposition de phase), on parle d’interférences constructives (resp. destructives).

Définition 1 : Différence de marche¶

On appelle différence de marche $\delta$ la différence de distance parcourue par les deux ondes avant d’arriver au point M :

\delta=S_{2} M-S_{1} M

(11)

L’amplitude de l’onde $s(M, t)$ est :

maximale si $\delta=m \times \lambda$ avec $m \in \mathbb{Z}$ ;
minimale si $\delta=\left(m+\frac{1}{2}\right) \times \lambda$ avec $m \in \mathbb{Z}$ .

III ) Interférences lumineuses¶

A) Spécificité des ondes lumineuses¶

L’observation d’interférences lumineuses demande une condition particulière : il faut utiliser une unique source lumineuse (on ne peut pas observer d’interférences entre des ondes issues de deux sources indépendantes). Le dispositif expérimental appelé interféromètre doit donc produire, à partir d’une seule source, deux ondes se superposant dans une zone de l’espace. Ces ondes issues d’une même source sont qualifiées de cohérentes.

Par ailleurs, les détecteurs lumineux (œil ou détecteur électronique) ne peuvent pas suivre les variations temporelles des signaux liés à la propagation de la lumière (d’une fréquence comprise entre 10¹⁴ et $10^{15} \mathrm{~Hz}$ ). Ils sont sensibles à l’intensité lumineuse moyenne (ou éclairement moyen) :

\mathcal{I}(M)=K\left\langle s(m, t)^{2}\right\rangle\left\langle s\left(M_{,} t\right)^{2}\right\rangle=\frac{1}{T} \int_{0}^{T} s(M, t)^{2} d t

(12)

avec $K$ une constante qui dépend de la géométrie du capteur. Dans toute la suite, on supposera donc que les deux sources étudiées sont issues d’une même source ponctuelle et monochromatique.

Remarque¶

Dans le cas d’une onde lumineuse, le signal $s(M, t)$ représente une composante du champ électrique.

Exercice de cours à connaître 4¶

Exprimer l’intensité lumineuse associée à une onde progressive sinusoïdale (donc monochromatique).

B ) Formule de Fresnel¶

On admet que la formule sur les amplitudes, trouvée dans la première partie du cours, est toujours valable dans le cadre des interférences lumineuses. On a donc :

A^{2}=A_{1}^{2}+A_{2}^{2}+2 A_{1} A_{2} \cos (\Delta \varphi)

(13)

Formule de Fresnel¶

En traduisant cette relation en termes d’intensité pour un capteur, on obtient la formule de Fresnel :

\mathcal{I}(M)=\mathcal{I}_{1}+\mathcal{I}_{2}+2 \sqrt{\mathcal{I}_{1} \mathcal{I}_{2}} \cos (\Delta \varphi)

(14)

avec :

$\mathcal{I}_{1}$ l’intensité produite par la source 1 ;
$\mathcal{I}_{2}$ l’intensité produite par la source 2 ;
$\mathcal{I}(M)$ l’intensité résultant de la superposition au point $M$ .

Remarque¶

Cette formule doit être rappelée dans un sujet de première année, mais elle sera à connaître en deuxième année.

C ) Différence de marche et chemin optique¶

On retrouve donc les mêmes conditions d’interférences que pour les ondes mécaniques, à partir du déphasage :

\Delta \varphi=\frac{2 \pi}{\lambda}\left(S_{2} M-S_{1} M\right)=\frac{2 \pi}{\lambda_{0}} n\left(S_{2} M-S_{1} M\right)

(15)

avec $\lambda$ la longueur d’onde de l’onde dans le milieu de propagation, $\lambda_{0}$ sa longueur d’onde dans le vide et $n$ l’indice optique du milieu.

Définition 2 : Chemin optique¶

Le chemin optique entre deux points $A$ et $B$ de l’espace dans un milieu d’indice $n$ est défini par :

(A B)=n A B

(16)

Exercice de cours à connaître 5¶

On considère deux rayons lumineux rectilignes et parallèles entre eux, dont l’un traverse une lame de verre d’épaisseur $e$ et d’indice optique $n$ . En dehors de cette lame de verre, on supposera que les rayons lumineux se propagent dans l’air d’indice $n_{\text {air }} \simeq 1$ . Les sources $S_{1}$ et $S_{2}$ sont à la distance $D$ d’un écran.

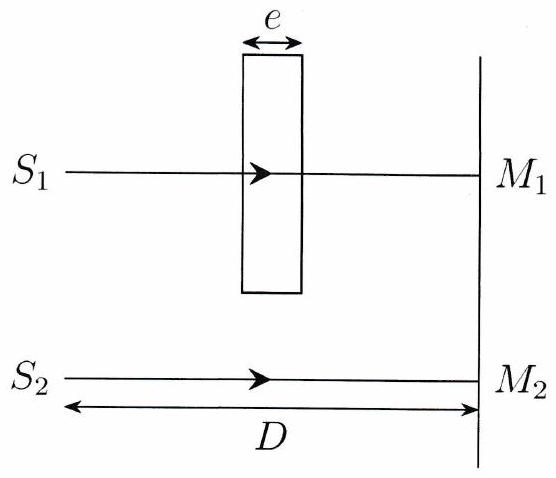
Pourquoi le rayon lumineux n’est-il pas dévié lors de son passage dans la lame en verre?
Calculer les chemins optiques $\left(S_{1} M_{1}\right)$ et $\left(S_{2} M_{2}\right)$ .

Ainsi la formule de Fresnel se réécrit :

\mathcal{I}(M)=\mathcal{I}_{1}+\mathcal{I}_{2}+2 \sqrt{\mathcal{I}_{1} \mathcal{I}_{2}} \cos \left(\frac{2 \pi}{\lambda_{0}} \delta(M)\right)

(17)

Avec $\lambda_{0}$ la longueur d’onde dans le vide et $\delta(M)$ la différence de chemin optique au point $M$ .

Remarque¶

La différence de chemin optique est l’équivalent de la différence de marche utilisée par les ondes mécaniques.

Exercice de cours à connaître 6¶

Récrire la formule de Fresnel dans le cas $\mathcal{I}_{1}=\mathcal{I}_{2}=\mathcal{I}_{0}$ (deux ondes de même intensité).

Le lieu des interférences constructives, c’est-à-dire l’ensemble des points où les ondes issues de $S_{1}$ et $S_{2}$ interfèrent constructivement, vérifie :

\Delta \varphi \equiv 0[2 \pi] \quad \Leftrightarrow \quad \delta(M)=m \lambda_{0} \quad \text { avec } \quad m \in \mathbb{Z}

(18)

où $\lambda_{0}$ est la longueur d’onde de la lumière dans le vide. De même, le lieu des interférences destructives vérifie :

\Delta \varphi \equiv \pi[2 \pi] \quad \Leftrightarrow \quad \delta(M)=\left(m+\frac{1}{2}\right) \lambda_{0} \quad \text { avec } \quad m \in \mathbb{Z}

(19)

D ) Les trous d’Young¶

Exercice de cours à connaître 7¶

On considère le dispositif représenté ci-dessous, placé dans l’air, éclairé par une source lumineuse ponctuelle monochromatique de longueur d’onde dans le vide $\lambda_{0}$ . On note $n$ l’indice de l’air dans lequel est plongé le dispositif.

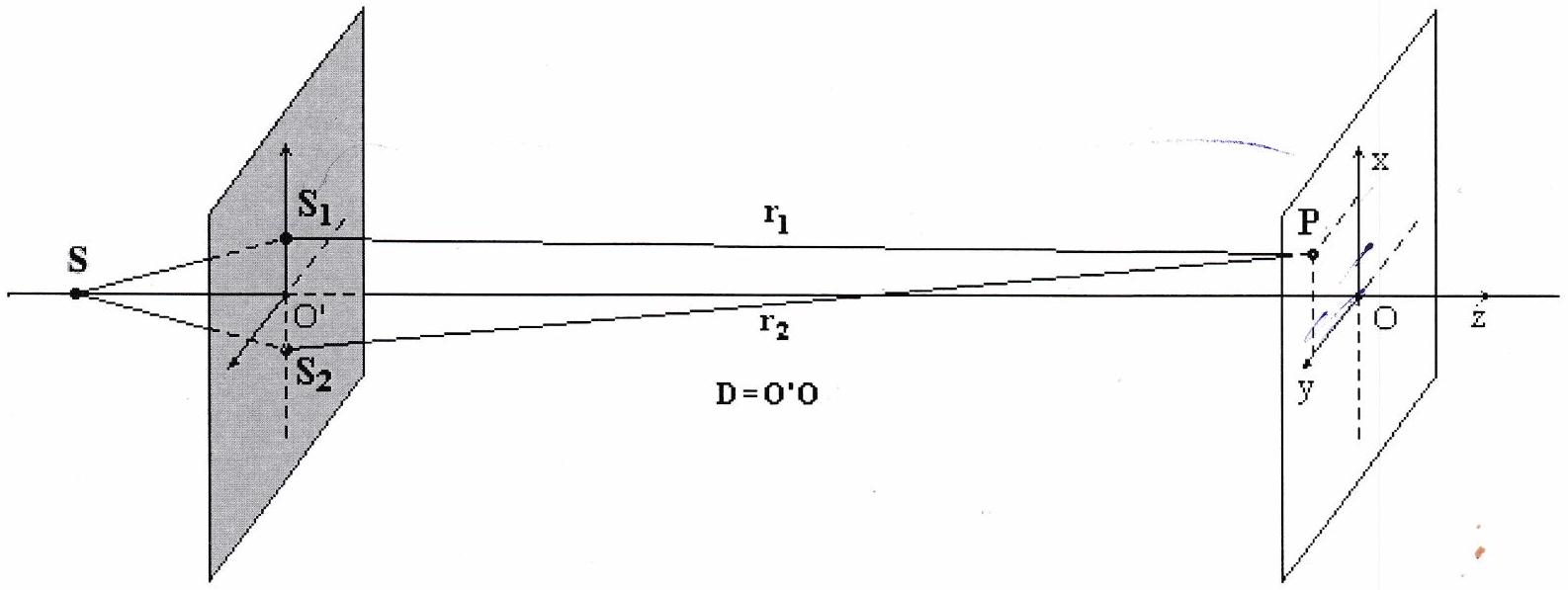
On suppose que le diamètre des deux trous identiques est suffisamment petit pour que tout l’écran soit éclairé uniformément par chacun des trous. La distance entre les deux trous est notée $a$ et on considère qu’ils sont symétriques par rapport au point $O^{\prime}$ .

Que peut-on dire de la différence de chemin optique entre la source $S$ et chacun des trous situés en $S_{1}$ et $S_{2}$ ?
Le point $P$ situé sur l’écran est repéré par ses coordonnées ( $x, y, z$ ). On suppose $a \ll D$ , ainsi que $|x| \ll D,|y| \ll D$ et $z=-D$ . Exprimer la différence de chemin optique $\delta(M)$ entre les chemins $\left(S S_{1} P\right)$ et $\left(S S_{2} P\right)$ .
En déduire l’allure de la figure d’interférence et la position des zones lumineuses.
Donner l’expression de l’interfrange $i$ , c’est-à-dire la distance entre deux maximums d’intensité lumineuse (resp. deux minimums) en fonction de $n, \lambda_{0}, D$ et $a$ . L’interfrange change-t-il si le dispositif est plongé dans l’eau ? Faire les applications numériques pour $\lambda_{0}=532 \mathrm{~nm}, D=1,0 \mathrm{~m}$ et $a=1,0 \mathrm{~mm}$ .
Quel serait l’effet d’une modification de la position de la source $S$ ?

Différence de chemin optique¶

Pour deux trous d’Young séparés d’une distance $a$ , la différence de chemin optique sur un écran situé à une distance $D$ s’exprime :

\delta(x)=n \frac{a x}{D}

(20)

où $x$ est l’abscisse d’un point de l’écran, avec l’axe ( $O x$ ) colinéaire à la droite passant par le centre des deux trous, et $n$ l’indice du milieu.

Interfrange¶

L’interfrange $i$ est la distance séparant deux franges claires (resp. deux franges sombres) de la figure d’interférence. Pour deux trous d’Young séparés par une distance $a$ éclairés par une source produisant une onde lumineuse monochromatique ponctuelle de longueur d’onde dans le vide $\lambda_{0}$ se propageant dans un milieu d’indice $n$ vers un écran situé à une distance $D$ , on a :

i=\frac{\lambda_{0} D}{n a}=\frac{\lambda D}{a}

(21)

Remarque¶

En pratique, la figure d’interférence obtenue à l’aide des trous d’Young est modulée par la figure de diffraction associée à un seul trou. Pour obtenir des images plus lumineuses, on remplace souvent les trous d’Young par des fentes fines. En dehors de la figure de diffraction, les résultats sont inchangés.