Chapitre 13¶

Ondes stationnaires¶

Jusqu’à présent, on a étudié des ondes se propageant dans un milieu “ouvert”. Lorsqu’un milieu est limité, les ondes atteignant les frontières du milieu vont donner naissance à des ondes réfléchies qui vont se superposer aux ondes incidentes.

Dans ce chapitre, nous allons donc nous intéresser à la superposition de deux ondes se propageant dans des directions opposées.

I ) Superposition de deux ondes progressives se propageant en sens contraire¶

A) Observations¶

Simulation 1 : Onde stationnaire¶

Animation : https://phyanim.sciences.univ-nantes.fr//Ondes/ondes_
stationnaires/stationnaires.php

Considérons deux ondes progressives sinusoïdales de même amplitude et même fréquence se propageant en sens contraire (onde incidente en vert et onde réfléchie en rouge). On s’intéresse à la superposition de ces deux ondes (en bleu). Qu’observez-vous ? $\_\_\_\_$ $\_\_\_\_$ $\_\_\_\_$ $\_\_\_\_$ $\_\_\_\_$

B) Calcul de l’onde résultante¶

On considère une onde $s_{1}(x, t)$ progressive sinusoïdale de fréquence $f$, d’amplitude $S_{0}$ et se propageant selon un axe ( $0 x$ ) vers les $x$ croissants. Dans la même zone de l’espace, on considère une deuxième onde $s_{2}(x, t)$ progressive sinusoïdale de même fréquence, de même amplitude mais se propageant vers les $x$ décroissants.

Exercice de cours à connaître 1¶

Les deux ondes décrites précédemment vont alors se superposer.

1. Donner l’expression des deux ondes $s_{1}(x, t)$ et $s_{2}(x, t)$.

2. En déduire l’expression de l’onde résultant de leur superposition :

II ) Ondes stationnaires¶

A) Définition¶

Définition 1 : Onde stationnaire¶

Une onde stationnaire résulte de la superposition de deux ondes progressives de même fréquence et de même amplitude, mais qui se propagent en sens opposé. Pour une onde stationnaire, les variables de temps et d’espace sont découplées. Ce type d’onde peut donc se mettre sous la forme :

De manière générale, une onde stationnaire sinusoïdale pourra s’écrire sous la forme :

La figure 13.1 représente $s(x, t)$ en fonction de $x$ à différents instants. On constate que cette onde ne se propage pas d’où le qualificatif de stationnaire.

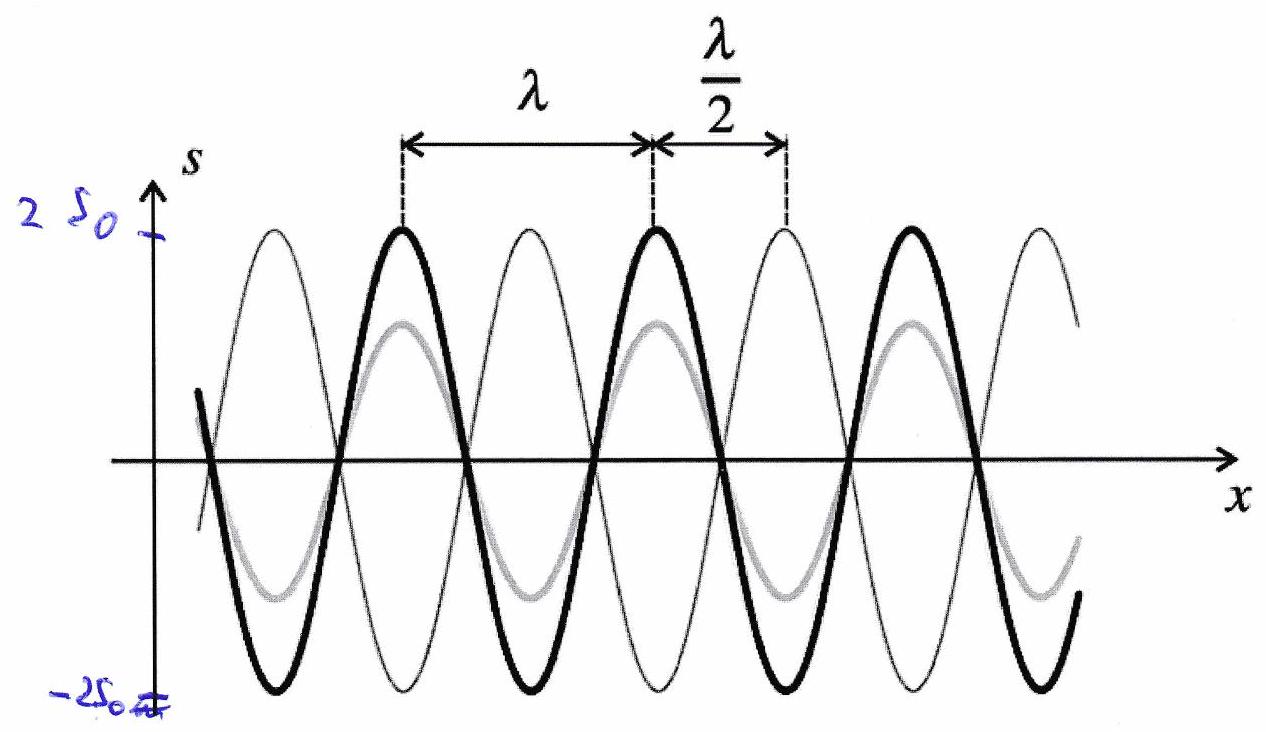
Figure 13.1: Onde stationnaire à trois instants différents : $t_{1}$ (en noir), $t_{2}$ (en gris clair) et $t_{3}=t_{1}+\frac{T}{2}$ (en gris foncé, trait fin).

Remarque¶

Une onde stationnaire ne se propage pas et ne véhicule donc pas d’énergie.

B ) Ventres et nœuds¶

Définition 2 : Ventre et nœud¶

Une onde stationnaire est composée :

• de ventres, correspondant aux points où l’amplitude de vibration est la plus grande ;

• de nœuds, correspondant aux points où l’amplitude de vibration est nulle à tout instant $t$.

Exercice de cours à connaître 2¶

On suppose une onde stationnaire de la forme :

1. Donner les différentes positions des nœuds.

2. Quelle est la distance entre deux nœuds consécutifs ?

3. Donner les différentes positions des ventres.

4. Quelle est la distance entre deux ventres consécutifs ?

5. Quelle est la distance entre un ventre et un nœud consécutif ?

Soit $\lambda$ la longueur d’onde d’une onde stationnaire.

• Deux nœuds consécutifs sont séparés par une distance $\frac{\lambda}{2}$;

• Deux ventres consécutifs sont séparés par une distance $\frac{\lambda}{2}$;

• Un ventre et un nœud consécutifs sont séparés par une distance $\frac{\lambda}{4}$.

L’existence de nœuds et de ventres de vibration est une propriété caractéristique des ondes stationnaires.

Remarque¶

On peut interpréter la présence de ventres et de nœuds en termes d’interférences constructives et destructives.

III ) Étude de la corde vibrante¶

A ) Oscillation libre d’une corde tendue et fixée à ses deux extrémités¶

1 ) Ondes stationnaires sur une corde de longueur $L$ finie¶

On s’intéresse à une corde de longueur $L$ fixée à ses deux extrémités en $x=0$ et en $x=L$. Il n’y a donc aucun déplacement vertical aux deux extrémités, ce qui impose les conditions aux limites :

On la lâche écartée de sa position d’équilibre et on la laisse vibrer librement.

Exemple¶

Corde d’un instrument de musique que l’on fait vibrer en la pinçant (guitare) ou en la frappant (piano).

Exercice de cours à connaître 3¶

Supposons que l’onde résultant de la superposition de l’onde incidente et de l’onde réfléchie en $x=0$ soit :

1. En utilisant la condition aux limites en $x=0$, donner la valeur du déphasage $\varphi$ entre l’onde incidente et l’onde réfléchie.

2. En déduire une nouvelle expression de $s(x, t)$ où les variables de temps et d’espace sont découplées.

3. En utilisant la condition aux limites en $x=L$, montrer que seules certaines valeurs de la pulsation spatiale $k$ sont possibles.

4. En déduire une condition sur la fréquence pour que l’onde stationnaire sinusoïdale puisque exister sur la corde.

Remarque¶

La réflexion est “parfaite”, car nous négligeons l’atténuation de l’onde, au cours de sa propagation.

Bilan¶

En régime libre, les fréquences d’une onde stationnaire sinusoïdale pouvant exister dans une corde de longueur $L$ dont les extrémités sont fixées ne prennent que des valeurs discrètes :

On dit qu’elles sont quantifiées. Il en va de même pour les longueurs d’onde :

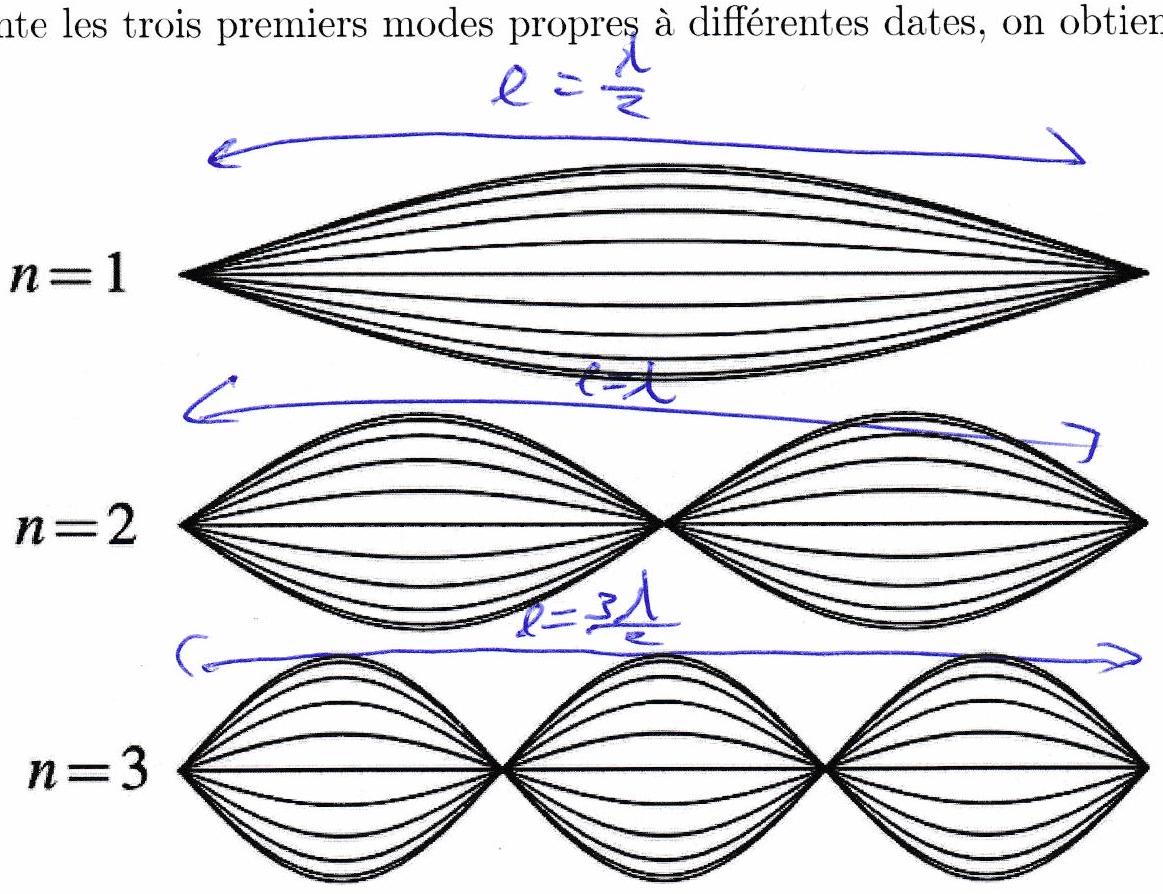
La fréquence $f_{1}$ est appelée fréquence du mode fondamental. La fréquence $f_{n}=n f_{1}$ pour $n \geq 1$ est la fréquence de l’harmonique de rang $n$. Les modes propres correspondent aux ondes stationnaires sinusoïdales pouvant exister dans une corde en accord avec les conditions aux limites:

C’est la limitation spatiale de l’onde qui entraîne une quantification des fréquences : seul un nombre discret de fréquences peuvent exister. Les valeurs des fréquences propres dépendent directement de la nature des conditions aux limites imposées à la corde. suivant :

2 ) Mouvement général de la corde¶

Le mouvement général d’une corde pincée ou frappé n’est pas sinusoïdal, c’est en fait une superposition des différents modes propres. L’oscillation libre d’une corde peut se mettre sous la forme d’une superposition linéaire de ses modes propres, et la vibration résultante s’écrit :

B ) Régime sinusoïdal forcé : Corde de Melde¶

1 ) Expérience de la corde de Melde¶

On tend une corde horizontale entre un vibreur et une poulie. La tension de la corde est déterminée par la masse $m$ que l’on accroche à l’extrémité pendante : si la poulie est sans frottement et que la masse est immobile, la tension de la corde est égale en norme à $m g$. La longueur utile de la corde, notée $L$, correspond à la distance entre le vibreur et la

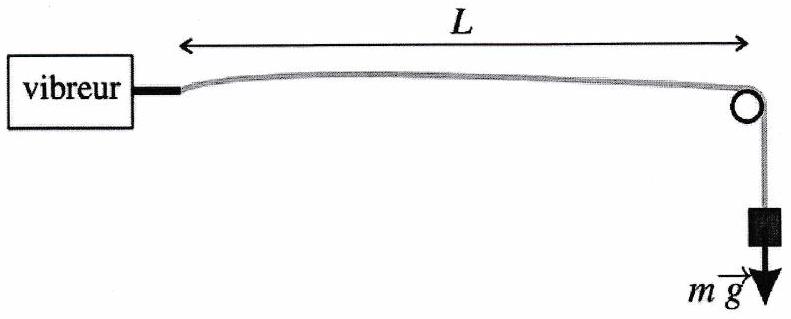
poulie.

Le vibreur est alimenté par un générateur de basses fréquences (GBF) et il impose à l’extrémité de la corde un mouvement sinusoïdal d’amplitude de l’ordre de quelques millimètres et dont la fréquence $f$ se règle sur le GBF .

Expérience 1 : Corde de Melde¶

À l’aide du GBF, on fait varier la fréquence d’excitation de la corde. Qu’observez-vous ? $\_\_\_\_$ $\_\_\_\_$ $\_\_\_\_$

2 ) Étude théorique¶

Exercice de cours à connaître 4¶

Dans l’étude de l’expérience précédente, on suppose que la perturbation imposée par le vibreur est de la forme $a \cos (\omega t)$. On cherche à former une onde stationnaire d’expression :

1. Donner l’expression des conditions aux limites pour l’expérience de la corde de Melde.

2. En déduire une relation entre l’amplitude du vibreur $a$ et celle de la corde $A$.

3. Donner la condition pour qu’on observe une résonance.

Ainsi, l’onde stationnaire devient résonnante (en régime forcé) lorsque la pulsation d’excitation du vibreur coïncide avec une des pulsations propres de vibration de la corde, exactement comme pour un circuit $L C$ série où la pulsation $\omega_{0}=\frac{1}{\sqrt{L C}}$ désigne à la fois la pulsation propre en régime libre et la pulsation de résonance en régime forcé.

IV ) Ondes stationnaires et instruments de musique¶

A) Hauteur et timbre d’un son¶

Le modèle précédent a permis d’établir l’expression des modes propres pour une corde fixée en ses deux extrémités. Nous pouvons directement l’appliquer aux instruments de la famille des cordes (guitare, piano, violon, etc.).

Le mouvement général de la corde n’est pas sinusoïdal, c’est une superposition des différents modes propres. L’oscillation libre d’une corde peut se mettre sous la forme d’une superposition linéaire de ses modes propres, et la vibration résultante s’écrit :

Définition 3 : Hauteur et timbre d’un son¶

• La hauteur du son est déterminée par sa fréquence, elle correspond à la fréquence du mode fondamental. Cette fréquence du fondamental correspond à la note jouée. Plus cette fréquence est faible, plus la note est grave et plus cette fréquence est élevée, plus la note est aiguë.

• Cependant, deux instruments différents peuvent jouer la même note et le ressenti sera différent. Le timbre du son est la propriété liée à cette différence. Le timbre d’un son est lié au nombre et à l’intensité des harmoniques présents.

B ) Instruments à cordes¶

On admet que la fréquence fondamentale d’une corde de longueur $L$ attachée à ces deux extrémités est :

avec $T$ la tension sous laquelle est tendue la corde (homogène à une force) et $\mu$ la masse linéique de la corde ( $\mathrm{en} \mathrm{kg} \cdot \mathrm{m}^{-1}$ ).

• Plus la longueur de la corde $L$ est petite, plus la fréquence fondamentale $f_{1}$ est grande et donc plus le son est aigu. C’est pour cela, par exemple, que l’on déplace son doigt sur les cordes d’une guitare ou d’un violon pour choisir la note à jouer. C’est aussi pour cela qu’un violon, plus petit qu’une contrebasse ou un violoncelle, joue des notes plus aiguës ;

• Plus une corde est tendue ( $T$ augmente), plus la fréquence fondamentale est élevée et donc plus le son est aïgu : c’est ce que l’on observe lorsqu’on accorde une guitare en tournant les clés correspondant à chaque corde ;

• plus la masse linéique $\mu$ est élevée, plus la fréquence fondamentale est basse et donc plus le son est grave : c’est pour cela que les cordes les plus graves d’un piano sont entourées de cuivre, qui permet d’obtenir un son plus grave que des cordes en acier.