Régime sinusoïdal forcé¶

Exercice 1 : Équivalences entre dipôles - ★¶

Les dipôles représentés ci-dessous sont étudiés en RSF à la pulsation $\omega$.

1. Déterminer, les valeurs de $R^{\prime}$ et $L^{\prime}$ pour lesquelles les deux dipôles sont équivalents, en fonction de $\omega$.

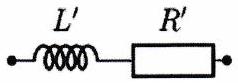
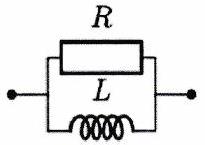
2. Si l’on remplace la bobine $L^{\prime}$ par un condensateur $C^{\prime}$, le dipôle $R^{\prime} C^{\prime}$ série peut-il être équivalent au dipôle $R L$ parallèle ? Justifier.

Exercice 2 : Résonance en tension dans un circuit $R L C$ ★¶

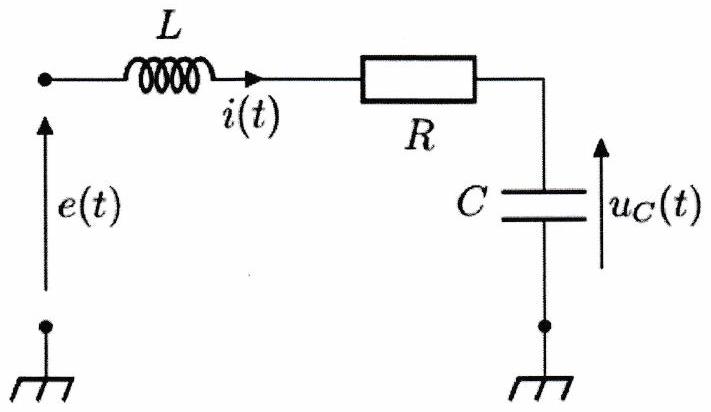
On considère le circuit $R L C$ série représenté ci-dessous où la tension $e(t)$ est de la forme

On s’intéresse à l’évolution de la réponse en tension aux bornes du condensateur, en régime permanent, en fonction de la pulsation $\omega$ de l’excitation $e(t)$.

1. Donner l’expression du signal complexe $\underline{e}(t)$ associé à $e(t)$.

2. Exprimer le signal complexe $\underline{u_{C}}(t)$ associé à $u_{C}(t)$ en fonction de $\underline{e}(t), \omega$ et des valeurs des composants.

3. En déduire l’équation différentielle vérifiée par la tension réelle $u_{C}(t)$. La mettre sous forme canonique et donner l’expression de la pulsation propre $\omega_{0}$ et du facteur de qualité $Q$ en fonction de $R, L$ et $C$.

On repasse en notation complexe et on note $\underline{H}(j \omega)$ le rapport $\frac{u_{C}}{\underline{e}}, G(\omega)$ son module et $\varphi(\omega)$ son argument :

4. Exprimer $\underline{H}(j \omega)$ en fonction de $\omega, \omega_{0}$ et $Q$.

5. Calculer les valeurs de $G(\omega)$ et $\varphi(\omega)$ pour $\omega=\omega_{0}$.

6. Montrer que $G(\omega)$ atteint un maximum pour une pulsation $\omega_{r}>0$ à condition que le facteur de qualité $Q$ soit suffisamment grand. Préciser cette condition à l’aide d’une inégalité sur $Q$ et donner l’expression de $\omega_{r}$.

7. Que peut-on dire de $\omega_{r}$ dans le cas où $Q \gg 1$ ?

8. Étudier le comportement asymptotique de $\underline{H}(j \omega)$ à basse fréquence et à haute fréquence. Les valeurs de $G(\omega)$ dans ces régimes sont-elles cohérentes avec les simplifications que l’on peut alors opérer dans le circuit ?

Exercice 3 : Paramètres d’une résonance - ★¶

On considère la résonance en intensité d’un circuit $R L C$ série, soumis à une tension d’entrée sinusoïdale $e(t)=E \cos (\omega t)$, avec $E=2,5 \mathrm{~V}$. L’amplitude $I_{m}$ de l’intensité est donnée cidessous, en échelles linéaire et semi-logarithmique.

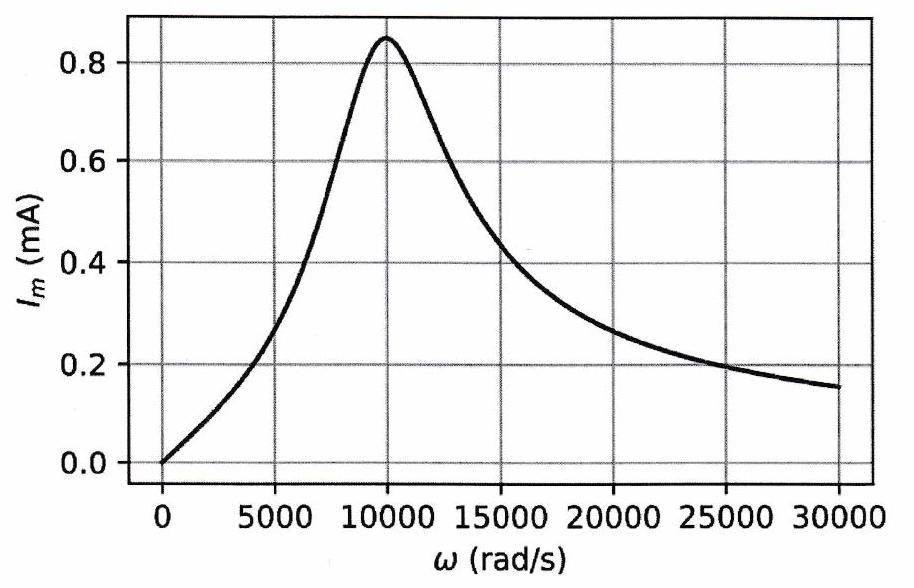
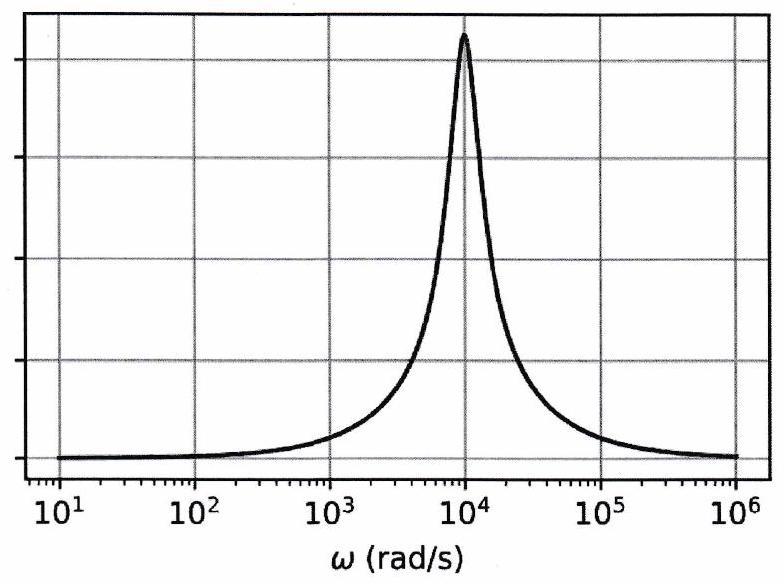
Déterminer les valeurs des composants $R, L$ et $C$.

Exercice 4 : Impédances équivalentes - ★★¶

Déterminer l’impédance équivalente à chacune des trois associations de dipôles suivantes.

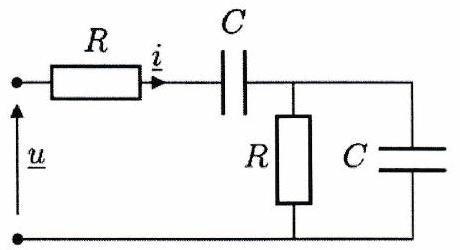
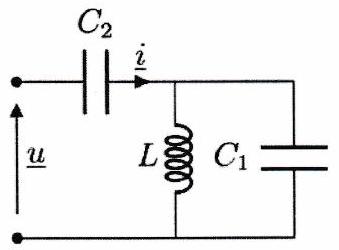
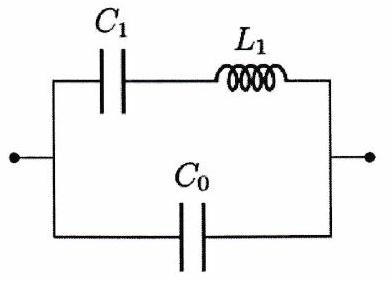
Exercice 5 : Intensité et tension en phase - ★★¶

On se place en régime sinusoïdal à la pulsation $\omega$. On souhaite que la tension $e(t)$ aux bornes du générateur ainsi que l’intensité $i(t)$ qui le traverse soient en phase.

Quelle condition doit-on vérifier ?

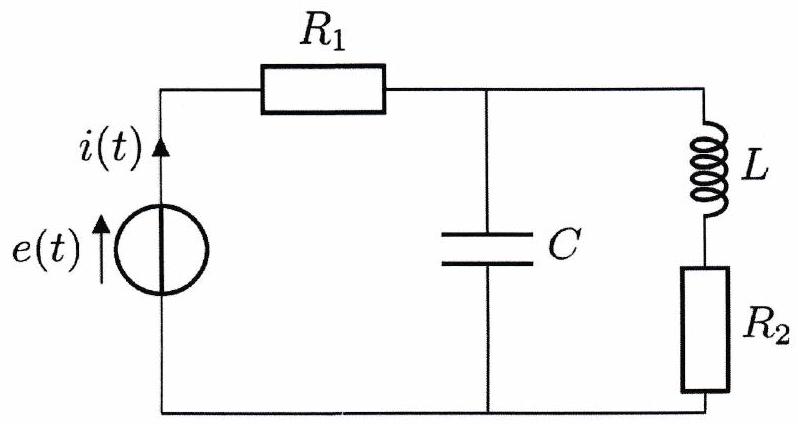
Exercice 6 : Circuit $R L C$ parallèle - ★★¶

On considère le circuit représenté ci-contre. Il est alimenté par un générateur de tension sinusoïdale :

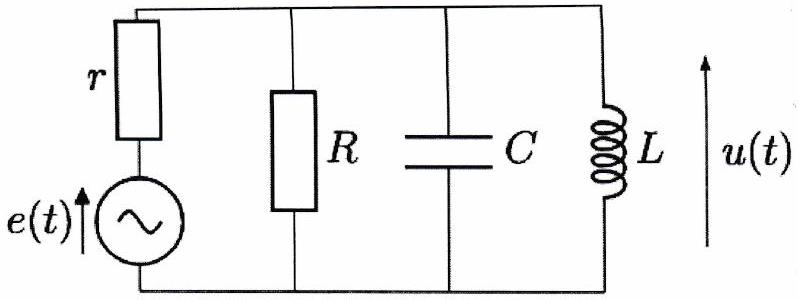
1. Déterminer les valeurs de l’amplitude $U_{m}$ de $u(t)$ à basse et haute fréquence en étudiant le comportement asymptotique des dipôles.

2. Établir l’expression de l’impédance complexe du dipôle $R L C$ parallèle.

3. Établir l’expression de l’amplitude complexe $\underline{U_{m}}$ de la tension $u(t)$ en fonction de $E_{m}, r$, $R, L, C$ et $\omega$.

La mettre sous la forme : $\underline{U_{m}}=\frac{A E_{m}}{1+j Q\left(\frac{\omega}{\omega_{0}}-\frac{\omega_{0}}{\omega}\right)}$, et identifier les expressions de $A, Q$ et $\omega_{0}$. 4. Justifier l’existence d’une résonance pour une pulsation que l’on exprimera. 5. Après avoir rappelé la définition de la bande passante, donner l’expression de sa largeur en fonction de $\omega_{0}$ et $Q$. 6. Pour quelle pulsation la tension $u(t)$ est-elle en phase avec le générateur $e(t)$ ?

Exercice 7 : Étude d’un circuit en régime sinusoïdal forcé - ★★¶

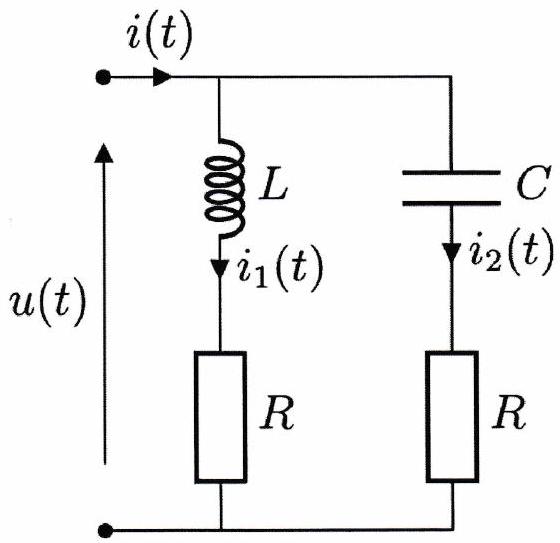
On étudie le circuit représenté ci-dessous où $u(t)=U_{m} \cos (\omega t)$. Dans l’exercice, on notera les intensités sous la forme $\underline{i}(t)=\underline{I} e^{j \omega t}$ et $I_{m}=|\underline{I}|$.

1. Déterminer l’impédance $\underline{Z}=\frac{\underline{u}}{\underline{i}}$ et l’admittance $\underline{Y}=\frac{1}{\underline{Z}}$.

2. Exprimer $\underline{i_{1}}(t)$ et $\underline{i_{2}}(t)$ en fonction de $\underline{i}(t)$.

3. Montrer que si le rapport des amplitudes complexes des intensités $\frac{I_{1}}{\bar{I}_{2}}$ est un imaginaire pur, les intensités 1 et 2 sont déphasées de $\frac{\pi}{2}$. Quelle relation lie alors $C, L$ et $R$ ?

4. Quelle relation vérifient $\omega, L$ et $C$ lorsque les amplitudes réelles des intensités sont égales $I_{m, 1}=I_{m, 2}$ ?

Exercice 8 : Circuit bouchon - $\star \star \star$¶

On considère le circuit ci-contre avec

On étudie la tension aux bornes de la résistance en régime sinusoïdal forcé :

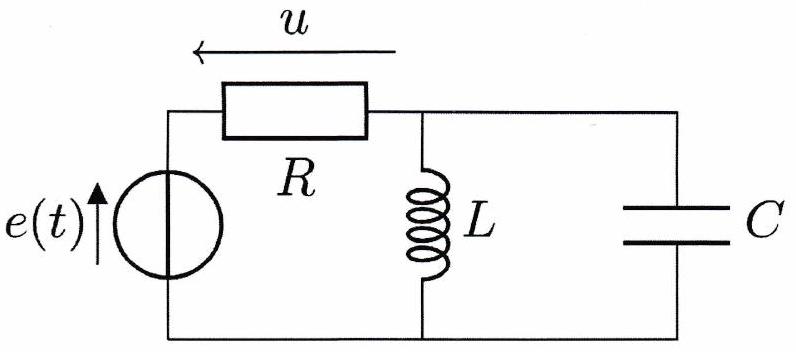
1. Établir l’expression de $\underline{u}$.

On introduira la pulsation caractéristique et le facteur de qualité. En déduire l’amplitude complexe $\underline{U_{0}}$ en fonction de $x=\frac{\omega}{\omega_{0}}$. 2. Montrer qu’il existe une pulsation pour laquelle l’amplitude $U_{0}$ est minimale.

Exercice 9 : Nature d’un dipôle inconnu - ★★★¶

Dans le montage ci-dessous, le GBF délivre une tension sinusoïdale $e(t)$ de fréquence $f . R$ est une résistance connue ( $R=100 \Omega$ ) et $\mathcal{D}$ un dipôle inconnu. On visualise à l’oscilloscope $v(t)$ et $u(t)$ avec des calibres identiques sur les deux voies.

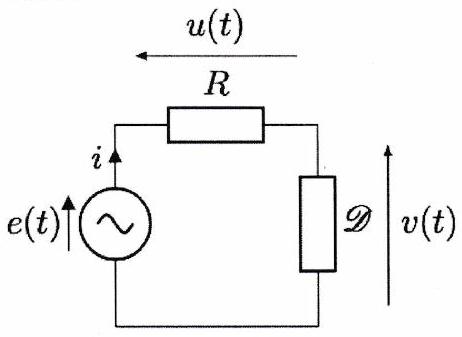
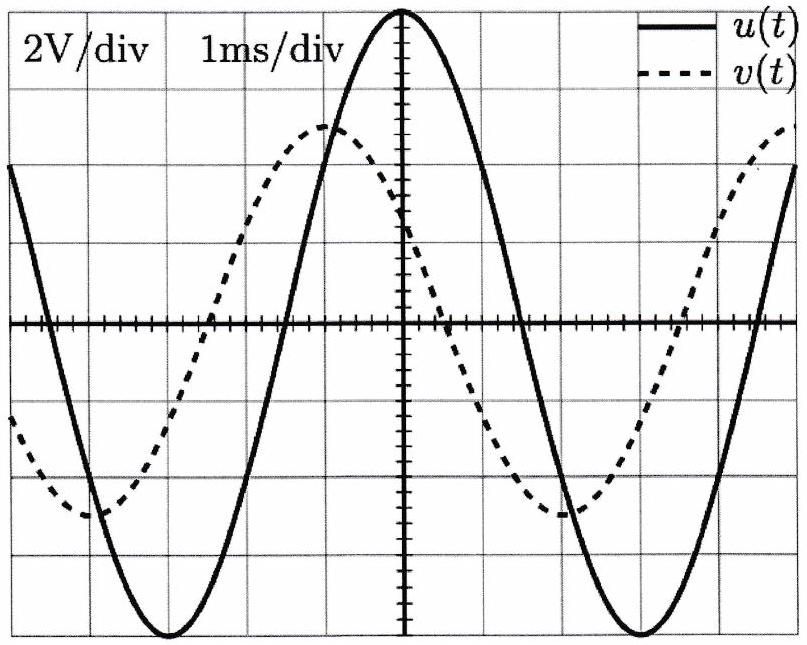
1. Sachant que le GBF et l’oscilloscope utilisés sont tous les deux munis de prises de terre, quel problème expérimental devra-t-on résoudre pour visualiser simultanément $v(t)$ et $u(t)$ ?

2. On note $\underline{Z}=X+j Y$ l’impédance du dipôle $\mathcal{D}$. Déterminer à partir de la courbe les valeurs de $X$ et de $Y$.

3. Par quel dipôle peut-on modéliser $\mathcal{D}$ ? Donner ses caractéristiques.