II ) Représentation complexe d’un signal
II ) Représentation complexe d’un signal¶
A ) Retour sur le circuit série¶
On considère un circuit soumis à une excitation sinusoïdale . La loi des mailles donne
avec .
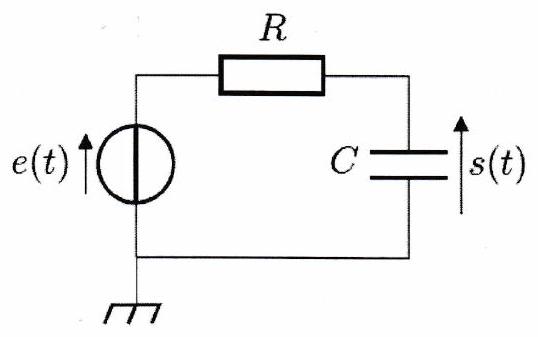
1 ) Solution de l’équation homogène¶
La solution de l’équation homogène est de la forme :
où dépend des conditions initiales.
Remarque¶
La solution de l’équation homogène donne l’allure du régime transitoire, dont l’étude a fait l’objet des deux chapitres précédents. Ici on ne s’intéresse qu’au régime permanent, c’est-à-dire le régime dont l’allure s’explique davantage grâce à la solution particulière.
2 ) Solution particulière¶
Le second membre n’est pas constant, donc la solution particulière n’est pas constante. En régime permanent, la réponse du circuit a la même allure que l’excitation : on cherche donc une solution particulière sinusoïdale et de même pulsation que l’excitation, c’est-à-dire de la forme :
où et dépendent des propriétés du signal , et notamment de sa fréquence. On peut trouver et en injectant la solution réelle dans l’équation différentielle avec second membre, mais il est beaucoup plus simple d’utiliser la notation complexe.
Définition 1 : Notation complexe¶
À un signal sinusoïdal de la forme , on associe le signal complexe noté tel que :
est appelé amplitude complexe du signal. En RSF à la pulsation , la solution particulière est entièrement déterminée par son amplitude complexe. Trouver la solution particulière revient donc à déterminer l’amplitude complexe du signal . En reprenant le cas du circuit , on peut passer en notation complexe :
On injecte la solution particulière dans l’équation différentielle du circuit avec second membre pour obtenir son amplitude complexe :
B) Utilisation de la notation complexe¶
En RSF à la pulsation , puisque le signal a la même pulsation que le signal , la connaissance de l’amplitude complexe suffit à caractériser entièrement . On peut ainsi déterminer :
l’expression du signal réel en prenant la partie réelle : ;
l’amplitude du signal réel en prenant le module : ;
la phase à l’origine en prenant l’argument : .
On peut ainsi représenter le l’amplitude complexe du signal dans le plan complexe.
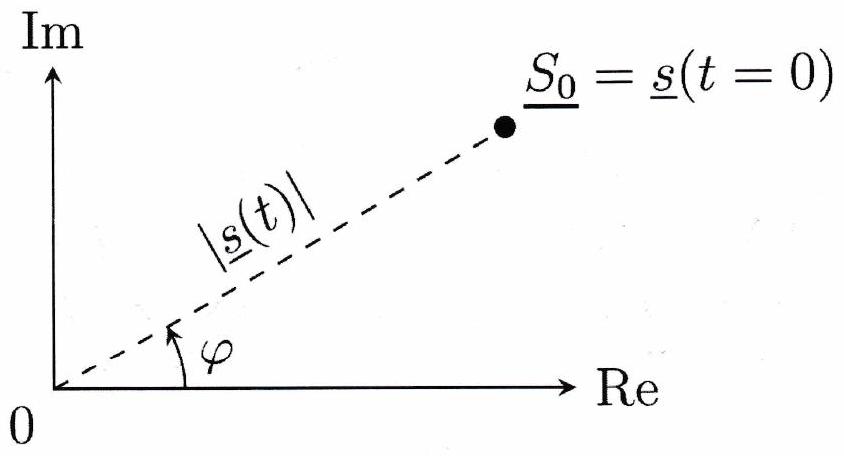
Toujours dans le plan complexe, tourne sur un cercle de rayon à la vitesse angulaire .
Remarque¶
L’argument d’un nombre complexe de partie réelle positive se calcule avec :
2 ) Dérivation et intégration d’un signal complexe¶
Exercice de cours à connaître 1¶
Démontrer que dériver ou primitiver un signal complexe de la forme se résume à une simple multiplication ou division par .
En RSF à la pulsation et en notation complexe :
dériver un signal revient à le multiplier par :
primitiver un signal revient à le diviser par :
3 ) Déphasage entre deux signaux¶
Soient deux signaux sinusoïdaux de même pulsation :
Le déphasage de par rapport à vaut et se calcule facilement en utilisant les amplitudes complexes :
Exercice de cours à connaître 2¶
Démontrer la formule précédente permettant de trouver le déphasage entre deux signaux à partir des amplitudes complexes.
Application 1¶
Donner l’amplitude complexe ou le signal réel dans les cas suivants, en supposant le régime sinusoïdal forcé de pulsation .
Application 2¶
À partir de l’amplitude complexe trouvée dans la partie A , donner l’expression de la solution réelle pour la tension aux bornes du condensateur dans un circuit série soumis à une tension sinusoïdale de pulsation .
III ) Impédance complexe¶
En RSF à la pulsation , on peut étudier simplement les circuits électriques en introduisant une généralisation complexe de la notion de résistance, appelée impédance.
Définition 2 : Impédance complexe¶
On appelle impédance complexe d’un dipôle, notée , la grandeur associée à la loi d’Ohm complexe, telle quẹ, en convention récepteur :
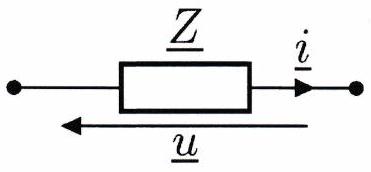
Remarque¶
Les parties réelles et imaginaires de l’impédance complexe s’expriment en Ohms.
Le module de l’impédance complexe est donné par :
avec l’amplitude de la tension aux bornes du dipôle et l’amplitude de l’intensité qui le traverse.
L’argument de l’impédance complexe donne le déphasage du signal par rapport au signal :
A ) Impédance complexe des dipôles usuels¶
1 ) Conducteur ohmique¶
En convention récepteur, l’impédance complexe d’un conducteur ohmique de résistance est :
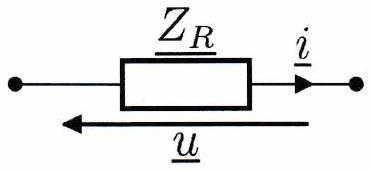
2 ) Condensateur¶
En convention récepteur, l’impédance complexe d’un condensateur de capacité est :
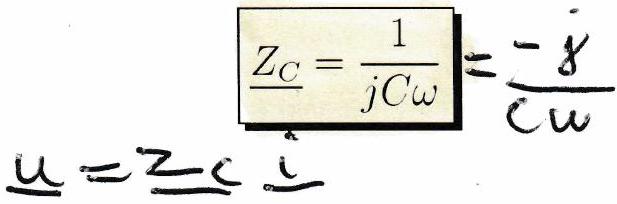
Remarque¶
L’impédance complexe d’un condensateur est un imaginaire pur. Son argument vaut , ce qui signifie que la tension aux bornes du condensateur est en retard de phase par rapport à l’intensité qui le traverse.
3 ) Bobine¶
En convention récepteur, l’impédance complexe d’une bobine d’inductance est:
Remarque¶
L’impédance complexe d’une bobine est un imaginaire pur. Son argument vaut , ce qui signifie que la tension aux bornes du condensateur est en avance de phase par rapport à l’intensité qui le traverse.
Exercice de cours à connaître 3¶
Démontrer les expressions des impédances complexes des trois dipôles précédents.
B ) Comportements asymptotiques¶
| Condensateur | Bobine | |
|---|---|---|
| Impédance | ||
| BF |

|

| | HF ( ) | | |
C) Association d’impédances¶
Les règles d’association d’impédances sont les mêmes que pour l’association de résistances.
L’association de deux impédances et en série est équivalente à une impédance :
De même, pour deux impédances en dérivation :
Exercice de cours à connaître 4¶
Démontrer les expressions des impédances complexes équivalentes dans le cas de deux résistances en série puis dans le cas de deux résistances en dérivation.
Application 3¶
Déterminer l’impédance complexe des dipôles représentés ci-dessous.
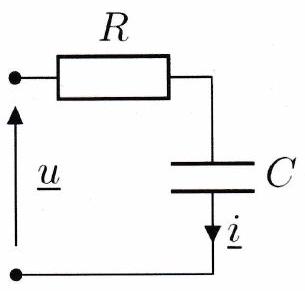
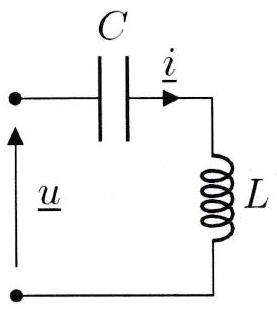
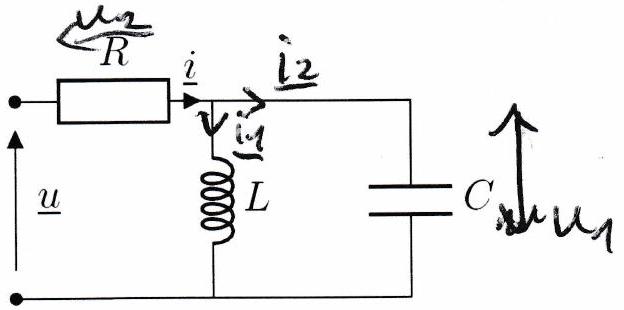
Dans l’approximation des régimes quasi-stationnaires (ARQS, cf. Ch3), on peut toujours utiliser les règles de base de l’électrocinétique : loi des mailles, loi des noeuds, ponts diviseurs, etc.
En notation complexe, les relations pour les ponts diviseurs de tension et d’intensité deviennent :
IV ) Résonances dans un circuit ¶
A) Résonance en intensité¶
1 ) Mise en évidence¶
On s’intéresse à un circuit série en RSF à la pulsation , alimenté par un générateur qui délivre une tension sinusoïdale . On s’intéresse à l’évolution de l’intensité du courant dans le circuit en fonction de la fréquence du signal d’excitation en mesurant la tension aux bornes de la résistance.
Simulation 1 : Résonance en intensité¶
resonance intensite.py
Commenter l’évolution de l’intensité du courant dans le circuit en fonction de la fréquence, en distinguant les régime basse et haute fréquence. Que remarque-t-on à la fréquence propre du circuit ?
△ On Li ace les Signanx en reginne permanlut.
△ On Li ace les Signanx en reginne permanlut.
Définition 3 : Résonance¶
L’excitation périodique d’un système oscillant à une pulsation proche de sa pulsation propre peut provoquer une réponse dont l’amplitude est maximale : c’est la résonance. La pulsation pour laquelle la réponse du système est maximale correspond à la pulsation de résonance.
Remarque¶
La pulsation de résonance n’est pas toujours égale à la pulsation propre de l’oscillateur !
2 ) Obtention de l’amplitude complexe¶
Exercice de cours à connaître 5¶
On s’intéresse au circuit représenté ci-dessous, alimenté par une tension .
Établir l’équation différentielle vérifiée par l’intensité .
L’écrire sous sa forme canonique et donner l’expression de la pulsation propre et du facteur de qualité .
En déduire l’expression de en régime permanent.
Retrouver cette relation en utilisant les notations complexes et un pont diviseur de tension.
Dans un circuit série de pulsation propre et de facteur de qualité , en à la pulsation , l’amplitude complexe de l’intensité du courant dans le circuit vérifie :
où est l’amplitude la tension aux bornes du générateur.
Remarque¶
On utilise souvent la pulsation réduite pour alléger la notation.
Comme le montre l’application précédente, utiliser la notation réelle permet aussi d’obtenir la relation voulue, mais la notation complexe simplifie le calcul. Utiliser la notation complexe permet ainsi d’obtenir facilement des équations différentielles autrement difficiles à établir.
3 ) Etude de l’amplitude complexe¶
Dans un circuit série en RSF , l’amplitude de l’intensité présente toujours un maximum. Il y a toujours résonance en intensité dans le circuit RLC série à la pulsation .
L’amplitude réelle de l’intensité en régime permanent se déduit de l’amplitude complexe en prenant le module :
Le calcul des limites permet d’avoir une idée de l’évolution de l’amplitude.
| Amplitude |
Le déphasage entre et est donné par :
Là encore, le calcul des limites permet d’avoir une idée de l’évolution du déphasage.
| Déphasage |
4 ) Évolution de l’amplitude complexe¶
Les équivalents basse et haute fréquence de l’amplitude complexe permettent d’étudier son comportement asymptotique.
| BF | Résonance | HF | |
|---|---|---|---|
| Équivalent |
Remarque¶
En calculant le module et l’argument avant de passer à la limite, on retrouve bien les résultats précédents.
Il est alors possible de représenter graphiquement l’amplitude complexe en distinguant module et argument.
Remarque¶
On peut aussi retrouver qualitativement les limites obtenues précédemment en raisonnant avec les circuits équivalents en basse et haute fréquence.
Définition 4 : Bande-passante¶
On définit la bande-passante comme la plage de fréquence sur laquelle l’amplitude de la réponse vérifie :
La largeur de la bande-passante est liée au facteur de qualité par la relation :
Expérimentalement, à partir de l’étude de la résonance en intensité on obtient :
la fréquence de propre :
en cherchant la fréquence de résonance pour laquelle est maximale ;
en cherchant la fréquence pour laquelle et sont en phase.
le facteur de qualité en mesurant la bande-passante, avec .
B) Résonance en tension aux bornes du condensateur¶
1 ) Mise en évidence¶
Toujours dans le circuit série, on s’intéresse cette fois à la tension aux bornes du condensateur en RSF à la pulsation .
Simulation 2 : Résonance en tension aux bornes du condensateur resonance_tension.py¶
Comparer la résonance en tension avec la résonance en intensité : y a-t-il toujours résonance ? La résonance se produit-elle toujours à la pulsation propre du circuit ? Commenter l’évolution de la pulsation de résonance quand devient grand. Commenter l’amplitude en basse fréquence. De quoi dépend l’amplitude à la pulsation ?
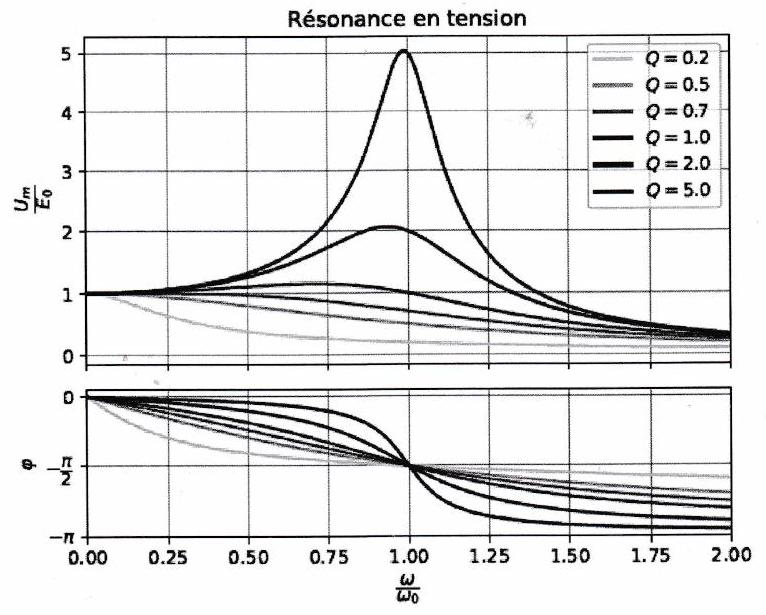
Dans un circuit série de pulsation propre et de facteur de qualité , l’amplitude complexe de la tension aux bornes du condensateur s’écrit :
où est l’amplitude de la tension aux bornes du générateur. On observe une résonance en tension aux bornes du condensateur seulement si :
La pulsation de résonance est inférieure à la pulsation propre .
Exercice de cours à connaître 6¶
Établir l’expression de la pulsation de résonance et en déduire la condition sur la valeur du facteur de qualité permettant une résonance en tension.
Remarque¶
Attention à ne pas confondre la condition de résonance en tension dans le circuit série avec la condition d’observation d’un régime transitoire pseudo-périodique ( ).
On parle aussi de résonance en charge car étudier la charge du condensateur revient à étudier la tension à ses bornes.
2 ) Evolution de l’amplitude complexe
| BF | HF | ||
|---|---|---|---|
| Équivalent | Vom | ||
| Amplitude | Um (wo) Eda | ||
| Déphasage |
3 ) Détermination expérimentale des paramètres du circuit¶
Expérimentalement, on obtient :
la fréquence propre :
en cherchant la fréquence pour laquelle et sont en quadrature de phase ( );
en cherchant la fréquence de résonance si est grand ;
le facteur de qualité :
en mesurant le rapport à la fréquence propre ;
en mesurant la bande-passante si est grand car on retrouve alors .
C ) Analyse de relevés expérimentaux¶
Le pic de résonance est d’autant plus étroit que le facteur de qualité est grand.
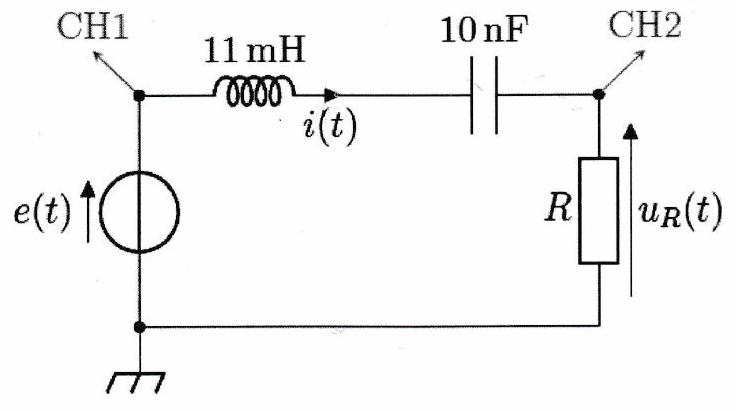
Exercice de cours à connaître 7¶
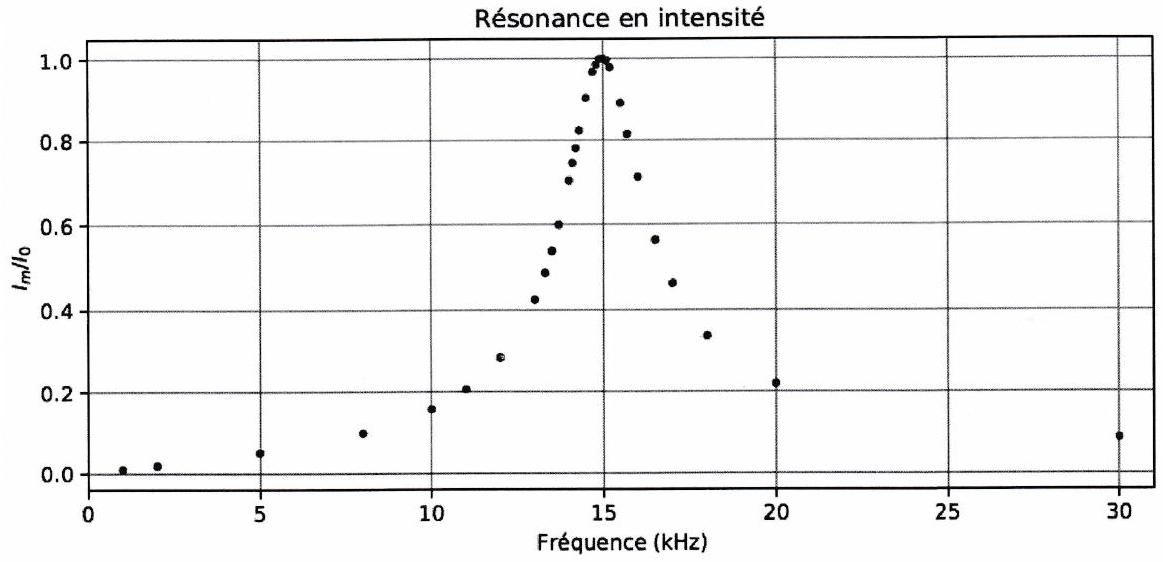
On réalise le circuit série représenté dans l’exercice de cours 5 avec une bobine d’inductance 11 mH . Le rapport est représenté ci-dessous, où est l’amplitude de l’intensité obtenue en mesurant la tension aux bornes de la résistance et sa valeur maximale.
Déterminer la fréquence de résonance et en déduire la valeur de la capacité .
Mesurer la largeur de la bande-passante. En déduire la valeur du facteur de qualité , puis la valeur de la résistance .
La résistance utilisée est en fait une résistance de . Commenter.
Le même condensateur est utilisé dans un autre circuit série avec une bobine et une résistance différentes. On mesure cette fois la tension aux bornes du condensateur et celle aux bornes du GBF pour tracer les courbes ci-dessous.
Résonance en tension
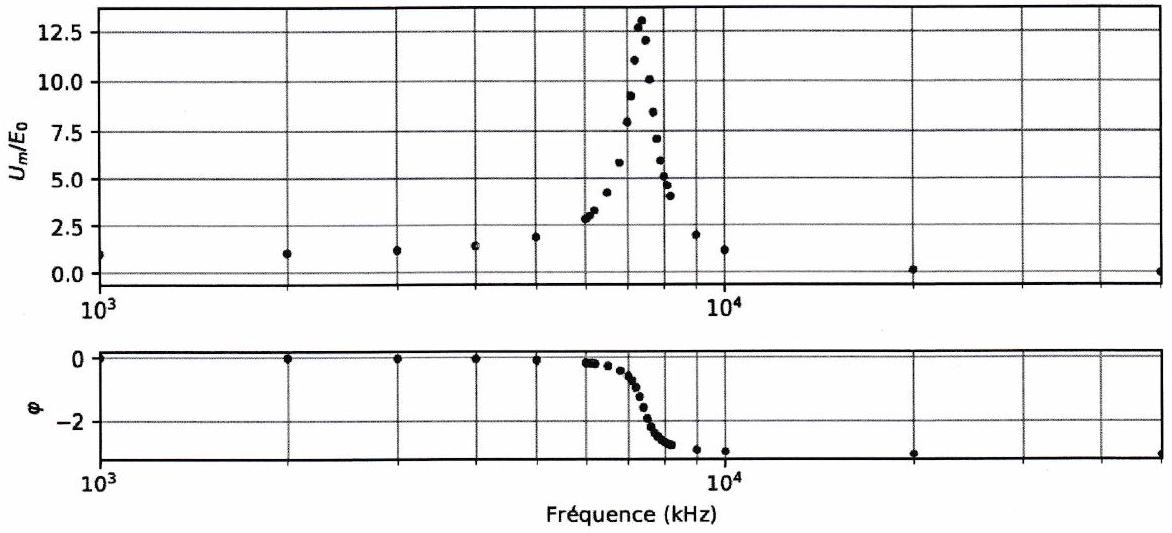
Mesurer la fréquence propre et le facteur de qualité de ce nouveau circuit.
La mesure de la bande-passante donne-t-elle un résultat compatible avec la valeur précédente du facteur de qualité ?
D ) Analogie électromécanique¶
Les outils introduits pour l’étude du circuit se généralisent à d’autres systèmes oscillants soumis à une excitation périodique, et notamment aux systèmes mécaniques.
| Circuit RLC | Masse-ressort |
|---|---|
| Charge ou tension Intensité Pulsation propre Facteur de qualité | Pojit-am X(F) Vitedse (V(H)) |
Le système masse-ressort présente toujours une résonance en vitart , mais on n’observe une résonance en p.o.s.r.t.o........ que si .
Annexe¶
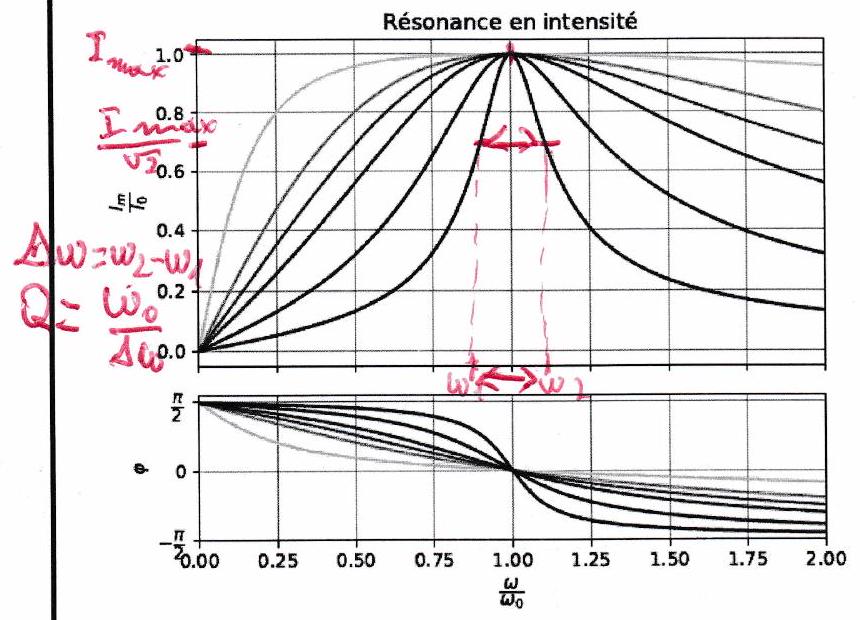
Document 1 : Résonances dans le circuit RLC série¶
Résonances en intensité et en tension aux bornes du condensateur dans un circuit série pour quelques valeurs du facteur de qualité . En particulier, on remarque qu’il existe une résonance en intensité en quelle que soit la valeur de , alors que la résonance en tension intervient à une pulsation et seulement si .
Document 2 : Relevés expérimentaux¶
Pour étudier la résonance en intensité dans un circuit série, on réalise le montage représenté ci-dessous et on relève simultanément les tensions aux bornes du GBF et de la résistance pour plusieurs fréquences d’excitation.
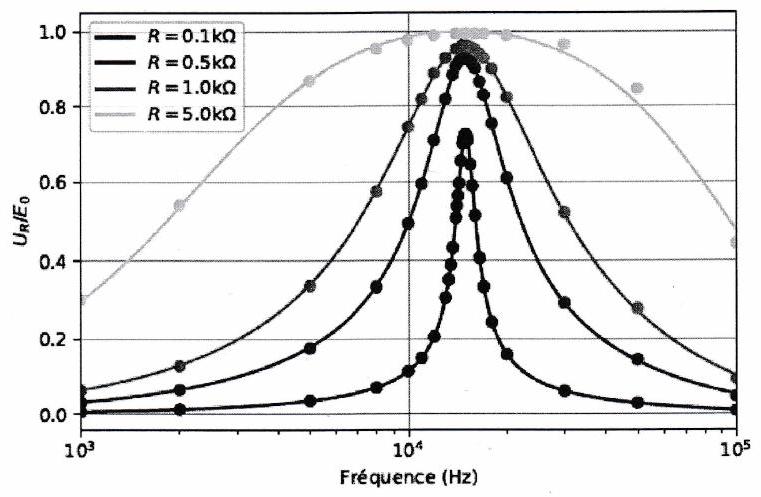
À résonance, le rapport est notablement différent de 1 pour les valeurs les plus faibles de la résistance, contrairement à ce que l’on s’attend à observer avec des composants idéaux. Ici, c’est la résistance de la bobine , de l’ordre de quelques dizaines de ohms pour des fréquences de l’ordre du kHz , qui explique l’écart observé. La largeur de la résonance est compatible avec cette valeur de résistance, qui s’ajoute à . Un modèle plus réaliste d’une bobine réelle est obtenu en associant un dipôle purement inductif d’inductance en série avec un conducteur ohmique de résistance . Dans le circuit étudié ici, l’ajout d’une résistance permet d’expliquer les résultats obtenus.