Chapitre 5¶

Oscillateur harmonique¶

Dans ce chapitre, on introduit un modèle physique qui produit un signal sinusoïdal appelé l’oscillateur harmonique. Ce modèle peut aussi bien s’appliquer à des systèmes :

• mécaniques : ressort, pendule, diapason, asservissement (SI) ;

• électroniques : quartz, ..

• optiques : laser, ...

• quantiques, ...

I ) Oscillateur harmonique mécanique¶

A ) Système étudié¶

Le système mécanique oscillant le plus simple est une masse accrochée à un ressort. Un mobile de masse $m$ se déplace sans frottement le long d’une tige horizontale. Sa position est repérée par l’abscisse $x(t)$ de son centre de masse $G$ mesurée sur l’axe ( $O x$ ) matérialisé par la tige. On choisit de placer l’origine de l’axe ( $O x$ ) de manière à ce que $G$ coïncide avec $O$ dans la position d’équilibre.

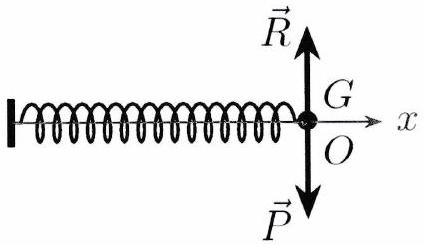
Équilibre

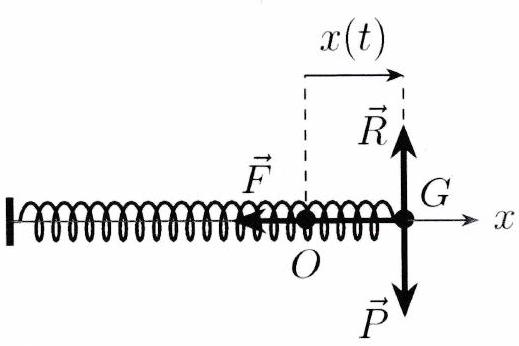
Mouvement

B ) Définition d’un oscillateur harmonique¶

Exercice de cours à connaître 1¶

Pour le système {ressort+masse} étudié, exprimer les forces s’exerçant sur le système puis appliquer le principe fondamental de la dynamique afin d’obtenir l’équation différentielle vérifiée par la position $x(t)$ du mobile de masse $m$.

L’équation différentielle ci-dessus est une équation différentielle d’oscillateur harmonique.

Définition 1 : Oscillateur harmonique¶

On appelle oscillateur harmonique un système physique décrit par une grandeur $x(t)$ dépendant du temps et vérifiant une équation différentielle de la forme :

où $\omega_{0}$ est une constante réelle positive qui est appelée pulsation propre de l’oscillateur $\omega=2 \pi \times f$ harmonique et qui s’exprime en $\mathrm{rad} \cdot \mathrm{s}^{-1}$. harmonique et qui s’exprime en $\mathrm{rad} \cdot \mathrm{s}^{-1}$.

Remarque¶

L’unité de $\omega_{0}$ se déduit de l’homogénéité de l’équation différentielle.

Le système $\{$ ressort + masse $\}$ étudié est un oscillateur harmonique, de pulsation propre :

C) Résolution de l’équation différentielle¶

Exercice de cours à connaître 2¶

La position $x(t)$ vérifie l’équation différentielle d’un oscillateur harmonique de pulsation $\omega_{0}$. Les solutions de l’équation de l’oscillateur harmonique peuvent s’écrire sous les formes :

1. Vérifier que la première forme est solution de l’équation différentielle de l’oscillateur harmonique.

2. Montrer que la deuxième forme est aussi solution et préciser la relation entre $\varphi$ et $\psi$.

3. Montrer que la dernière forme est équivalente à la première, et donc à la deuxième en utilisant les formules d’addition. Exprimer $A$ et $B$ en fonction de $x_{m}, \varphi$ et/ou $\psi$.

La solution générale de l’équation différentielle d’un oscillateur harmonique de pulsation propre $\omega_{0}$

peut s’écrire sous les formes :

où $(A, B)$ ou $\left(x_{m}, \varphi\right)$ sont des constantes qui dépendent des conditions initiales.

Pour résoudre l’équation différentielle d’un oscillateur harmonique, on applique la même méthode que pour résoudre une EDL1. Seule la forme de la solution de l’équation homogène change.

1. Écrire la solution générale de l’EDL2 ;

2. Déterminer les constantes d’intégration en exploitant les conditions initiales :

3. Conclure en donnant la solution de l’équation.

Remarque¶

Calculer la solution d’une équation différentielle du deuxième ordre requiert la connaissance de deux conditions initiales.

Application 1¶

Dans le cas du mobile accroché au ressort, les conditions initiales sont :

• la position initiale : $x(0)=x_{0}$;

• la vitesse initiale : $\frac{\mathrm{d} x}{\mathrm{~d} t}(0)=v_{0}$

Résoudre l’équation différentielle de l’oscillateur harmonique dans le cas du système {masse + ressort $\}$ étudié.

D ) Signal sinusoïdal¶

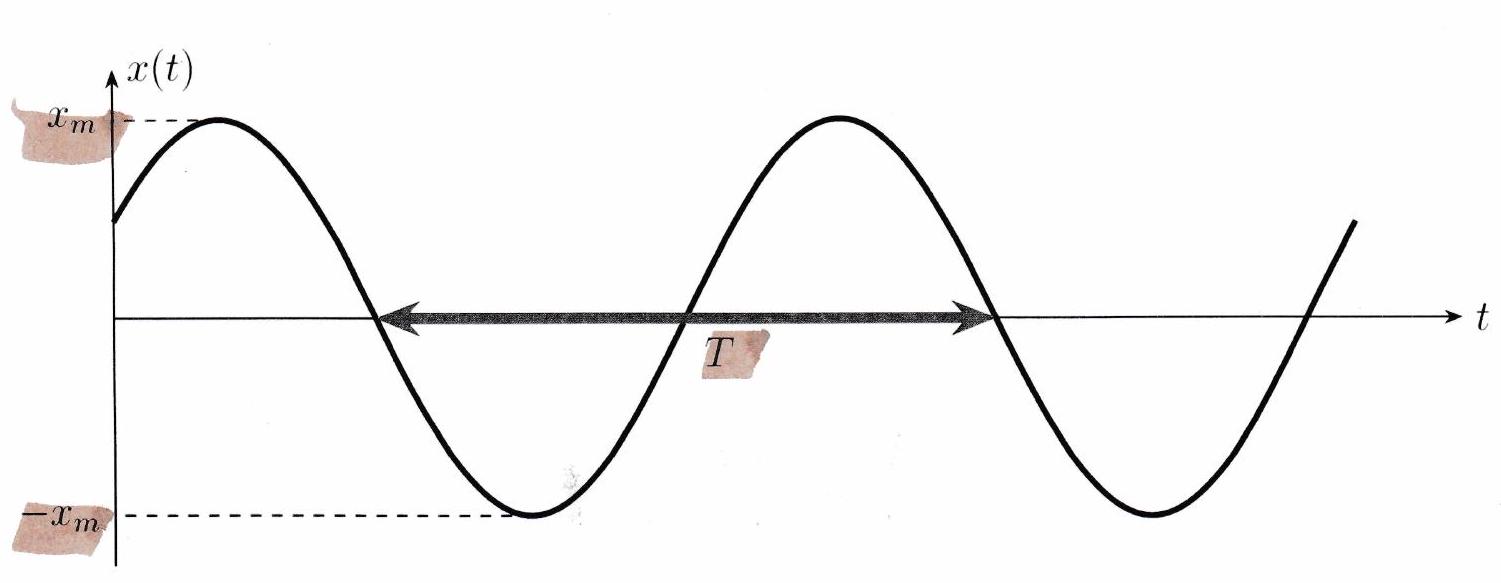
La position $x(t)$ du système s’écrit d’une manière générale sous la forme ci-dessous.

Un signal sinusoïdal est un signal de la forme :

où $A$ et $\omega$ sont des constantes positives et $\varphi$ une constante. $\omega$ est la pulsation du signal, $A$ son amplitude et $\varphi$ sa phase initiale (ou déphasage).

1 ) Amplitude du mouvement¶

Définition 2 : Amplitude¶

L’amplitude $A$ du mouvement est la valeur maximale atteinte par $s(t)$. On peut montrer que pour le système {masse - ressort} étudié l’amplitude du signal $x(t)$ est :

2 ) Période et fréquence¶

La période $T$ (en s) et la pulsation $\omega\left(\right.$ en $\left.\mathrm{rad} \cdot \mathrm{s}^{-1}\right)$ sont reliées par la formule : $T=\frac{2 \pi}{\omega}$ La fréquence $f(\mathrm{enHz})$ est donnée par : $f=\frac{1}{T}$; elle représente le nombre de répétitions du signal par unité de temps. La fréquence est donc reliée à la pulsation par : $f=\frac{\omega}{2 \pi}$ ou $\omega=2 \pi f$ Dans le cas du système {masse + ressort} étudié, on a :

Remarque¶

La périodicité du mouvement vient de la périodicité des fonctions cosinus et sinus.

3 ) Phase instantanée et phase initiale¶

Définition 3 : Phase instantanée¶

L’argument de la fonction cosinus est appelée phase instantanée, elle vaut donc $\omega t+\varphi$. La phase initiale $\varphi$ donne la valeur de départ du signal à $t=0$. Elle dépend donc de l’origine des temps choisie. De plus, le cosinus étant une fonction périodique de période $2 \pi$, la phase initiale n’est définie qu’à un multiple de $2 \pi$ près. On peut donc toujours se ramener à une phase initiale comprise entre $-\pi$ et $\pi$.

4 ) Déphasage¶

Le déphasage entre deux signaux de même fréquence est une information importante. Ce déphasage est lié au décalage temporel entre ces deux signaux.

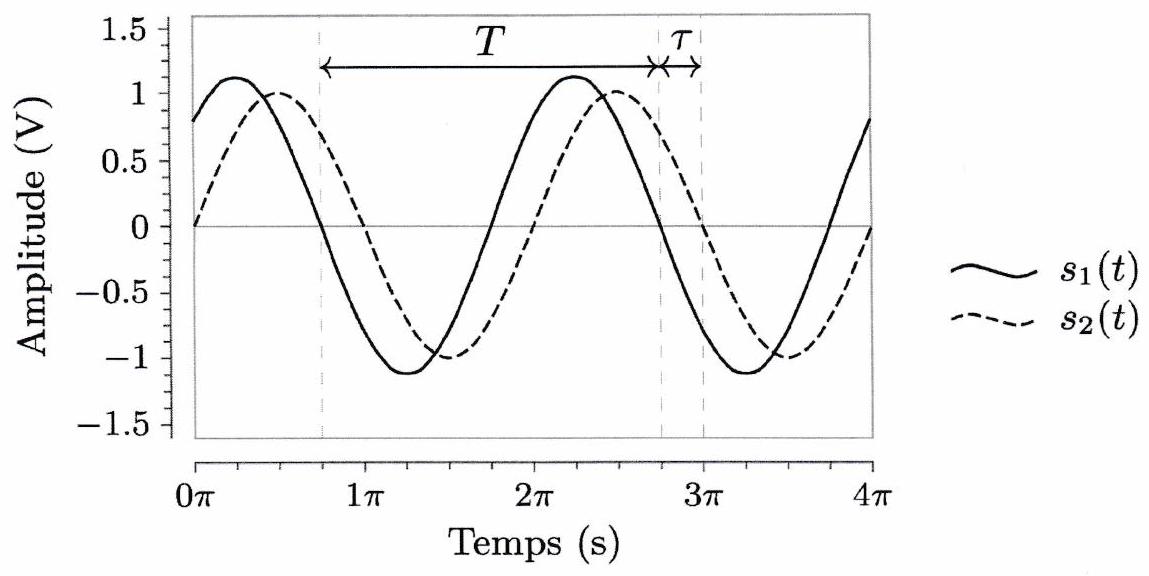
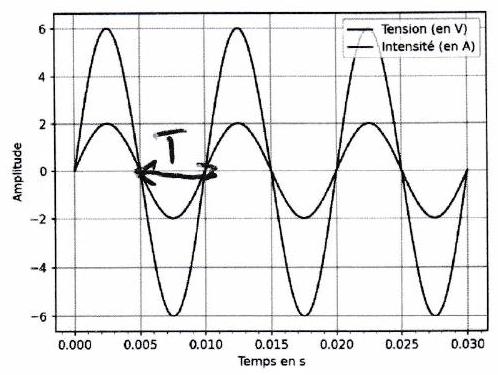
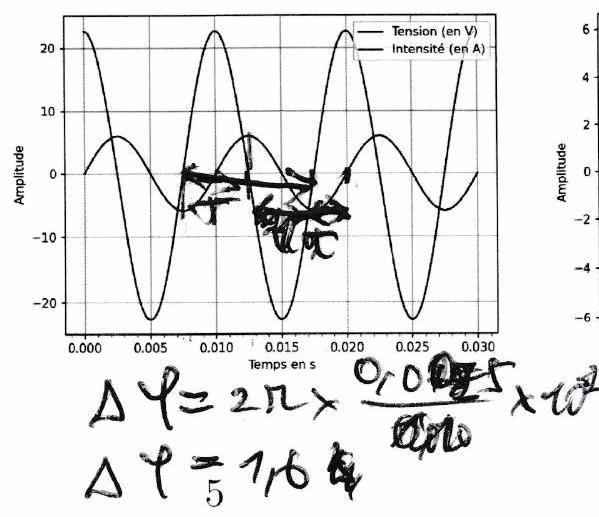
Méthode : Mesure du déphasage de $s_{2}$ par rapport à $s_{1}$¶

1. Repérer deux instants $t_{1}$ et $t_{2}$ consécutifs où le signal $s_{1}(t)$ s’annule avec la même pente. Cela nous permettra de calculer la période du signal.

2. Repérer un instant $t_{3}$ le plus proche possible de $t_{2}$ où le signal $s_{2}(t)$ s’annule avec la même pente que $s_{1}(t)$. Cela nous permettra d’évaluer le décalage temporel.

3. En déduire :

• La période $T=t_{2}-t_{1}$

• Le décalage temporel $\tau=t_{3}-t_{2}$

• Le déphasage $\Delta \varphi$ de $s_{2}$ par rapport à $s_{1}: \Delta \varphi=2 \pi \times \frac{\tau}{T}=2 \pi \times \frac{t_{3}-t_{2}}{t_{2}-t_{1}}$

Remarque¶

• On cherchera généralement le déphasage de la tension par rapport à l’intensité.

• Le déphasage $\Delta \varphi$ est positif si $s_{1}(t)$ est en avance par rapport à $s_{2}(t)$ et négatif si $s_{1}(t)$ est en retard.

Application 2¶

Donner les déphasages de la tension par rapport à l’intensité pour les trois dipôles cidessous.

1. Résistance

2. Bobine

3. Condensateur

II ) Oscillateur harmonique électrique¶

A) Circuit $L C$ libre¶

Le circuit étudié comporte une bobine d’inductance $L$ en série avec un condensateur de capacité $C$. Le condensateur est initialement chargé sous une tension $E$. On ferme l’interrupteur à la date $t=0$. Pour $t>0$, le condensateur se décharge dans la bobine, ce qui crée un courant $i(t)$.

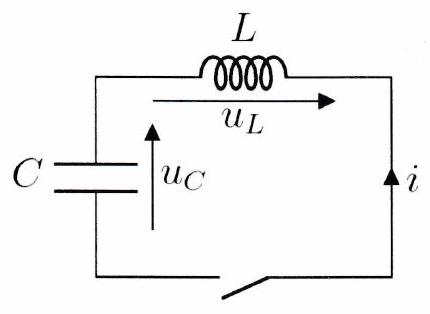
Exercice de cours à connaître 3¶

1. Établir l’équation différentielle vérifiée par la tension $u_{C}(t)$ pour $t \geq 0$.

2. Donner la dimension de $\sqrt{L C}$.

3. Comment pourrait-on obtenir l’équation différentielle vérifiée par la charge du condensateur $q(t)$ ? Et par l’intensité du courant $i(t)$ ?

4. Donner les valeurs de l’intensité $i(t)$ et de la tension $u_{C}(t)$ en $t=0^{+}$. Justifier.

5. En déduire les deux conditions initiales portant sur $u_{C}(t)$ et sa dérivée première.

6. Déterminer l’expression des constantes d’intégration puis exprimer la solution $u_{C}(t)$.

Dans un circuit $L C$ série, la tension aux bornes du condensateur, sa charge et l’intensité dans le circuit vérifient l’équation d’un oscillateur harmonique de pulsation propre

B) Bilan énergétique¶

Exercice de cours à connaître 4¶

suite de l’exercice de cours 3

1. Donner l’expression de la tension aux bornes du condensateur $u_{C}(t)$ et de l’intensité du courant $i(t)$ pour $t \geq 0$.

2. En déduire l’expression de l’énergie $\mathcal{E}_{C}(t)$ stockée par le condensateur et celle $\mathcal{E}_{L}(t)$ emmagasiné par la bobine en fonction du temps.

3. Montrer qu’à tout instant $\mathcal{E}_{C}(t)+\mathcal{E}_{L}(t)=\mathcal{E}_{0}$, où $E_{0}$ est l’énergie stockée par le condensateur avant la fermeture de l’interrupteur.

L’énergie d’un système électrique dépourvu de résistance, donc sans effet Joule, se conserve au cours du temps.

Les deux composants s’échangent l’énergie contenue dans le système {condensateur + bobine}, sans dissipation :

• quand le condensateur se comporte comme un générateur, on a $\mathcal{P}_{L}=-\mathcal{P}_{C}$ : la puissance fournie par le condensateur est intégralement reçue par la bobine ;

• quand la bobine se comporte comme un générateur, on a $\mathcal{P}_{C}=-\mathcal{P}_{L}$ : la puissance fournie par la bobine est intégralement reçue par le condensateur.

III ) Exemple : Réponse d’un circuit $L C$ à un échelon de tension¶

Pour résoudre l’équation différentielle d’un oscillateur harmonique avec second membre, on applique la même méthode que pour résoudre une EDL1. Seule la forme de la solution de l’équation homogène change.

1. Écrire la solution générale de l’équation homogène $u_{C, h}(t)$ (solution de l’oscillateur harmonique) ;

2. Trouver une solution particulière $u_{C, p}(t)$ (constante si le second membre l’est);

3. Exprimer la solution générale de l’EDL2 $u_{C}(t)=u_{C, h}(t)+u_{C, p}(t)$;

4. Déterminer les constantes d’intégration en exploitant les conditions initiales

5. Conclure en donnant la solution de l’équation.

Exercice de cours à connaître 5¶

On considère le circuit représenté ci-contre, composé d’un générateur idéal de tension de f.é.m. $E$, d’une bobine d’inductance $L$ et d’un condensateur de capacité $C$. À l’instant $t=0$, on ferme l’interrupteur.

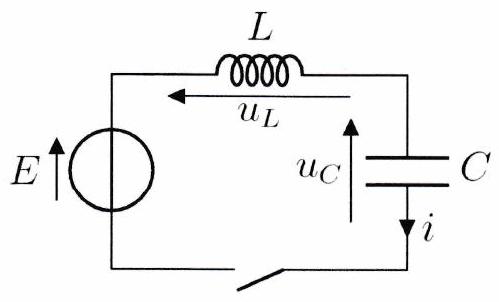
1. Établir l’équation différentielle vérifiée par la tension $u_{C}(t)$ pour $t \geq 0$.

2. Après résolution de l’équation différentielle, exprimer $u_{c}(t)$ en fonction des constantes de l’énoncé.

3. Représenter graphiquement $u_{C}(t)$ et faire apparaître la période $T$, l’amplitude $U_{1}$ et la valeur moyenne de ce signal $U_{0}$. Exprimer ces paramètres en fonctions de $E$, $L$ et $C$.