TD 12¶

Phénomènes d’interférences¶

Exercice 1 : Mesure de la vitesse du son - ★¶

Le trombone de Koenig est un dispositif de laboratoire permettant de faire interférer deux ondes sonores ayant suivi des chemins différents. Le haut-parleur, alimenté par un générateur de basses fréquences, émet un son de fréquence $f=1500 \mathrm{~Hz}$. On mesure le signal à la sortie avec un microphone branché sur un oscilloscope. En déplaçant la partie mobile $T_{2}$, on fait varier l’amplitude du signal observé. Elle passe deux fois de suite par une valeur minimale

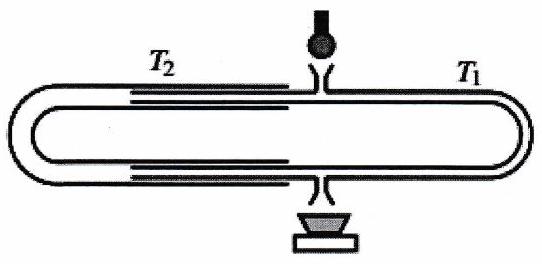
lorsqu’on déplace $T_{2}$ de $d=11,5 \pm 0,2 \mathrm{~cm}$. Déterminer la valeur de la célérité du son dans l’air à $20^{\circ} \mathrm{C}$, température de l’expérience.

Exercice 2 : Contrôle actif du bruit en conduite - ★¶

On s’intéresse à un système conçu pour l’élimination d’un bruit indésirable transporté par une conduite. Le bruit est détecté par un premier micro dont le signal est reçu par un contrôleur électronique. Le contrôleur, qui est le centre du système, envoie sur un haut-parleur la tension adéquate pour générer une onde de signal exactement opposé à celui du bruit de manière à ce que l’onde résultante au point $A$ (voir figure) et en aval de

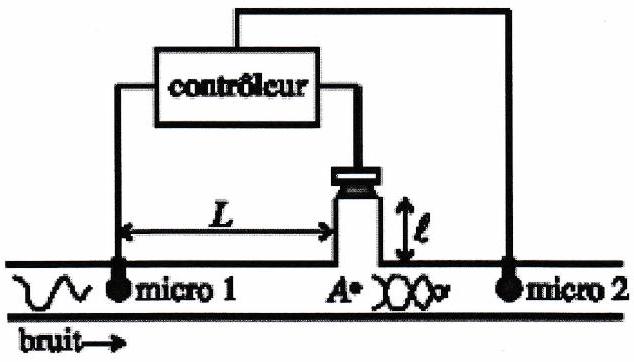
$A$ soit nulle.

1. Exprimer, en fonction de $L, l$ et de la célérité $c$ du son, le temps disponible pour le calcul du signal envoyé au haut-parleur.

2. On suppose le bruit sinusoïdal de pulsation $\omega$. On appelle $\varphi_{1}$ la phase initiale du signal détecté par le micro 1 et $\varphi_{\mathrm{HP}}$ la phase initiale du signal émis par le haut-parleur. Exprimer, en fonction de $\omega, c, L$ et $l$, la valeur que doit avoir $\Delta \varphi=\varphi_{\mathrm{HP}}-\varphi_{1}$.

3. L’onde émise par le haut-parleur se propage dans la conduite dans les deux sens à partir de $A$. Expliquer l’utilité du micro 2.

Exercice 3 : Trous d’Young - ★★¶

On étudie le dispositif des trous d’Young. Deux trous séparés d’une distance $a=0,10 \mathrm{~mm}$, sont éclairés par une lumière de longueur d’onde dans le vide $\lambda=450 \mathrm{~nm}$. Un écran est situé à une distance $D=20 \mathrm{~cm}$, où l’on étudie l’intensité lumineuse au point $M(x, y)$. L’ensemble est dans l’air, d’indice optique $n \simeq 1$. Dans toute la suite, on se place dans l’approximation paraxiale c’est-à-dire que $|x| \ll D$ et $a \ll D$.

1. (a) Donner l’expression de la différence de chemin optique entre les ondes issues des deux trous en $M$. (b) En utilisant la formule de Fresnel, exprimer l’éclairement $\mathcal{I}(x)$ sur l’écran. (c) Préciser l’expression de l’interfrange $i$, c’est-à-dire la distance sur l’écran entre deux interférences constructives successives, en fonction de $\lambda, D$ et $a$. Application numérique. (d) Exprimer $\mathcal{I}(x)$ en fonction de $i$. Que représente $i$ pour la fonction $x \mapsto \mathcal{I}(x)$ ? (e) Tracer l’allure de $x \mapsto \mathcal{I}(x)$.

2. On considère maintenant que les deux trous sont de diamètre différent. Le trou $S_{2}$ est plus large et laisse passer une onde lumineuse d’amplitude double de celle qui passe par $S_{1}$. (a) En utilisant la formule de Fresnel, exprimer l’éclairement $\mathcal{I}(x)$ sur l’écran. (b) $\mathcal{I}(x)$ s’annule-t-il ? (c) Tracer l’allure de $x \mapsto \mathcal{I}(x)$.

3. On se replace dans le cas où les trous sont de même diamètre. Une lame de verre à faces parallèles d’épaisseur $e$ inconnue et d’indice $n=1,57$ est positionnée en sortie du trou $S_{1}$. On suppose qu’au vu de la faible inclinaison des rayons, la lame de verre est traversée en incidence normale. (a) Montrer que la différence de chemin optique en un point $M$ de l’écran s’écrit :

(b) Déterminer la position $x_{c}$ sur l’écran de la frange centrale correspondant à $\delta(M)=0$. De quelle distance, et dans quel sens, s’est déplacée cette frange par rapport au cas où la lame est absente ? (c) En déduire l’expression de l’épaisseur $e$ de la lame en fonction de $x_{c}, a, D$ et $n$. Faire l’application numérique pour $x_{c}=28,5 \mathrm{~cm}$. (d) À quelle difficulté se heurte-t-on si l’on essaye de réaliser cette expérience en laboratoire?

Exercice 4 : Interférences ultrasonores - ★★¶

Une expérience d’interférences d’ondes ultra-sonores est réalisée en plaçant deux émetteurs $E_{1}$ et $E_{2}$ cote à cote relié à un même générateur. La fréquence d’émission est égale à 40 kHz , ce qui correspond à une longueur d’onde $\lambda=8,5 \mathrm{~mm}$. À part à la question 3 , les sources émettent des ondes en phase. On note $O$ le point milieu du segment délimité par les émetteurs distants de $a=4 \mathrm{~cm}$, et ( $O x$ ) l’axe situé sur la médiatrice de ce segment. On déplace le microphone sur un grand cercle de rayon $R=$

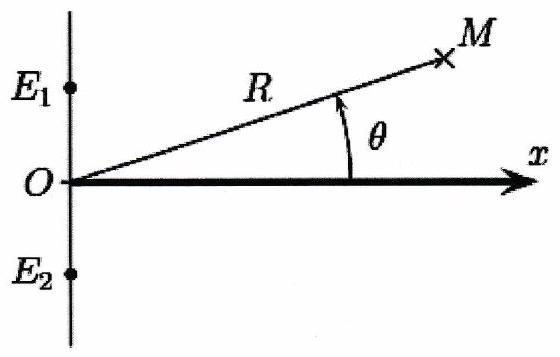
$0,5 \mathrm{~m}$ et on relève l’évolution de l’amplitude mesurée en fonction de l’angle $\theta$ que fait le vecteur $\overrightarrow{O M}$ avec l’axe $x$.

1. Distance interfrange : (a) Faire une figure pour un angle $\theta$ faible mais non nul. Rajouter sur la figure l’arc de cercle de centre $M$ passant par $E_{1}$, on note $H$ son intersection avec la droite ( $E_{2} M$ ). Que représente $E_{2} H$ ? (b) Montrer que les distances $E_{1} M$ et $E_{2} M$ peuvent s’écrire :

(c) On admet la formule suivante : si $\varepsilon \ll 1$, alors $\sqrt{1+\varepsilon} \simeq 1+\frac{1}{2} \varepsilon$. On se place dans le cas où $a \ll R$, montrer que $E_{1} H \simeq a \sin (\theta)$ puis en déduire le déphasage entre les ondes reçues en $M$ en fonction de $\theta, a, \lambda$. (d) Quelles sont, dans l’intervalle $\left[-30^{\circ}, 30^{\circ}\right]$, les valeurs de $\theta$ où on observe un maximum d’amplitude résultante ? 2. Minima d’amplitude (a) Sur l’intervalle d’étude précédent, quelles sont les positions où un minimum d’amplitude est attendu? (b) Si les ondes reçues ont même amplitude, quelle valeur d’amplitude minimale est prévue par la théorie ? (c) Quels défauts peuvent expliquer un écart entre prévision et observation ? 3. Un dispositif permet d’inverser le signal émis par l’un des émetteurs (ce qui revient à le déphaser de $\pi$ ). (a) Quel est l’état d’interférence sur l’axe ( $O x$ ) ? (b) Quelles sont les positions des nouveaux points de maximum et de minimum d’amplitude ? (c) Qu’advient-il si l’on inverse également l’autre signal ?