Chapitre 8¶

Filtrage linéaire : Principe¶

Il arrive fréquemment que l’on souhaite supprimer ou seulement modifier l’importance d’une partie des fréquences présentes dans un signal : on parle alors de filtrage.

Exemple¶

Supprimer un grésillement (en général de haute fréquence) dans un enregistrement ;
Supprimer des fréquences au-delà d’une certaine valeur dans un enregistrement audio : c’est le principe utilisé en compression audio MP3, où les hautes fréquences, peu audibles et qui ne contiennent pas d’information musicale essentielle, sont supprimées afin d’alléger la taille du fichier sonore ;
Sélectionner une station de radio, ce qui nécessite de sélectionner une plage précise de fréquences autour de la fréquence d’émission de la station.

I ) Signaux périodiques¶

Définition 1 : Signal périodique¶

Un signal $s(t)$ est périodique s’il existe une période $T$ minimale telle que $s(t+T)=s(t)$ .

A ) Valeur moyenne¶

La valeur moyenne d’un signal s’interprète bien graphiquement.

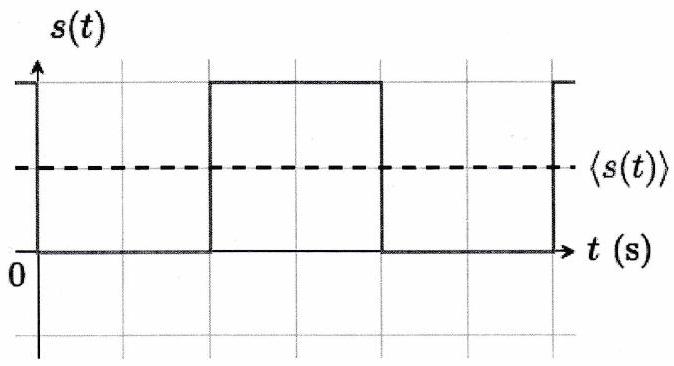
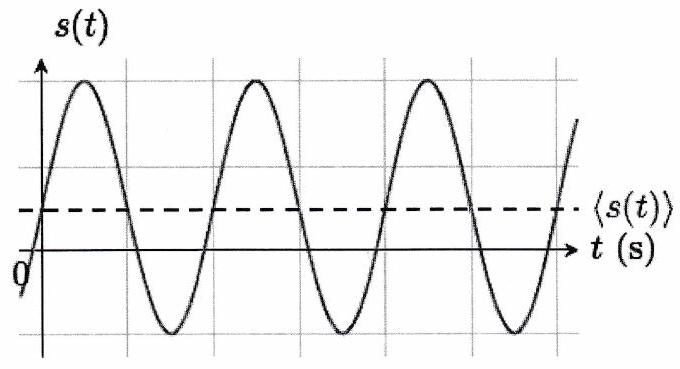
Définition 2 : Valeur moyenne¶

La valeur moyenne d’un signal périodique $s(t)$ , notée $\langle s(t)\rangle$ , est définie par :

\langle s(t)\rangle=\frac{1}{T} \int_{t_{0}}^{t_{0}+T} s(t) \mathrm{d} t

(1)

Remarque¶

$\langle s(t)\rangle$ ne dépend pas de $t_{0}$ . Le choix de $t_{0}$ est donc arbitraire : on prend la valeur qui nous arrange (souvent 0 ) !
Dans le cas d’un signal échantillonné sur une période, on approche la valeur moyenne par :

\langle s(t)\rangle \simeq \frac{1}{N} \sum_{k=1}^{N} s_{k}

(2)

Quand le nombre $N$ d’échantillons devient très grand, cette expression est équivalente à la précédente.

Application 1¶

Rappeler l’expression de la période $T$ d’un signal sinusoïdal de pulsation $\omega$ .
Exprimer puis calculer la valeur moyenne des signaux suivants : (a) $s_{1}(t)=S_{0}+S_{1} \cos (\omega t)$ (b) $s_{...