Propagation d’un signal¶

Exercice 1 : Quelques signaux - ★¶

Les questions sont indépendantes.

1. Donner la période $T$, la fréquence $f$, la pulsation $\omega$, l’amplitude $A$, la longueur d’onde $\lambda$, le nombre d’onde $k$, la célérité $c$ et la phase à l’origine $\varphi_{0}$ de l’onde :

où $t$ est en secondes et $x$ en mètres.

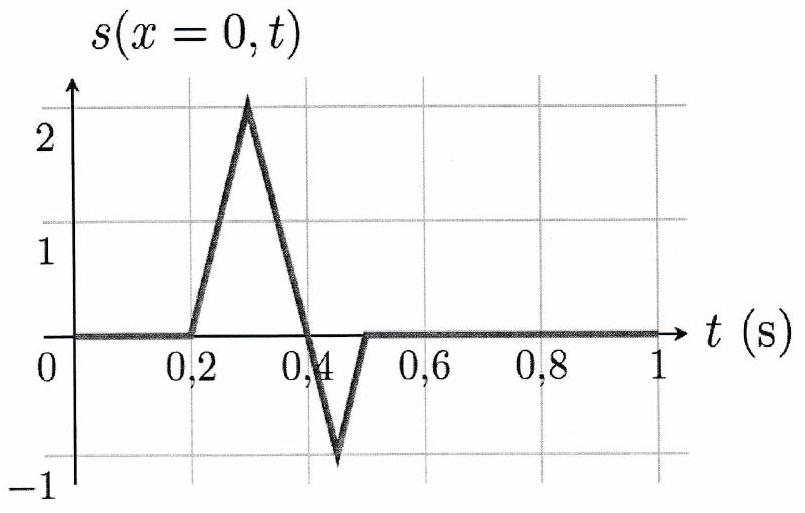
Une onde progressive se propage le long d’une corde à la célérité $c=50 \mathrm{~cm} \cdot \mathrm{~s}^{-1}$ vers les $x$ croissants. En $x=0$ (point A de la corde), on crée le signal représenté sur le schéma. 2. Déterminer la durée et la longueur de la perturbation. Représenter le signal $s_{M}(t)$ mesuré en $M$ avec $A M=25 \mathrm{~cm}$. Tracer ensuite $s(x, t=1 \mathrm{~s})$ et $s(x, t=2 \mathrm{~s})$.

3. Les chauve-souris émettent généralement une suite de cris en forme de trains d’onde, chacun d’une durée d’environ 3 ms et une fréquence porteuse variant entre 30 kHz et 100 kHz . Généralement, le temps $t$ entre deux cris est de 70 ms . À quelle distance maximale un objet peut-il être situé pour que l’écho d’un cri soit reçu avant l’émission du cri suivant ?

Exercice 2 : Ondes électromagnétiques - ★¶

Les antennes qui émettent des ondes électromagnétiques, ou qui les reçoivent, doivent avoir une longueur de l’ordre de la longueur d’onde $\lambda$ des ondes émises. On choisit généralement un sous-multiple comme $\frac{\lambda}{4}$ ou $\frac{\lambda}{8}$.

1. Pour transmettre la radio, on pourrait envisager d’émettre des signaux électromagnétiques ayant les mêmes fréquences que les sons audibles (audiofréquences), entre 20 Hz et 20 kHz . Calculer les longueurs d’onde dans l’air de telles ondes électromagnétiques. Conclure.

On donne la célérité de la lumière dans le vide $c=3,00 \cdot 10^{8} \mathrm{~m} \cdot \mathrm{~s}^{-1}$ et on considérera qu’elle est identique dans l’air. 2. On transforme alors ces signaux par un procédé appelé “modulation de fréquence” (FM), qui leur donne des fréquences beaucoup plus élevées, entre 87 MHz et 108 MHz . Calculer les longueurs d’onde dans l’air des ondes de radio FM, et en déduire l’ordre de grandeur de la taille des antennes nécessaires.

Exercice 3 : Ondes progressives sinusoïdales - ★¶

1. On étudie une onde d’équation :

où $s$ s’exprime en $\mathrm{cm}, t$ en s et $z$ en m . (a) Donner l’amplitude, la période, la fréquence, la pulsation, le vecteur d’onde (norme direction et sens), et la longueur d’onde de l’onde. (b) Dans quelle direction et dans quel sens se propage-t-elle? Quelle est sa célérité? 2. Une onde sinusoïdale se propage dans la direction des $x$ croissants avec la célérité $c$. En $x=0$, on a :

Donner l’expression de $s(x, t)$ et tracer l’allure du signal temporel perçu en $x=\frac{\lambda}{4}$. 3. Une onde sinusoïdale se propage dans la direction des $x$ décroissants avec la célérité $c$. À $t=0$, on a :

Donner l’expression de $s(x, t)$ et tracer l’allure des variations spatiales du signal à $t=\frac{T}{4}$. 4. Une onde sinusoïdale se propage dans la direction de l’axe ( $O x$ ) dans le sens des $x$ croissants à la célérité $c$. (a) L’expression du signal de l’onde au point d’abscisse $x_{1}$ est $s_{1}\left(x_{1}, t\right)=A \cos (\omega t)$. En déduire l’expression de $s_{1}(x, t)$. Représenter $s_{1}(x, 0)$ en fonction de $x$. (b) On donne $s_{2}(0, t)=A \sin (\omega t)$. Déterminer l’expression de $s_{2}(x, t)$. Représenter graphiquement $s_{2}\left(\frac{\lambda}{2}, t\right)$ en fonction de $t$.

Exercice 4 : Exploitation de battements -¶

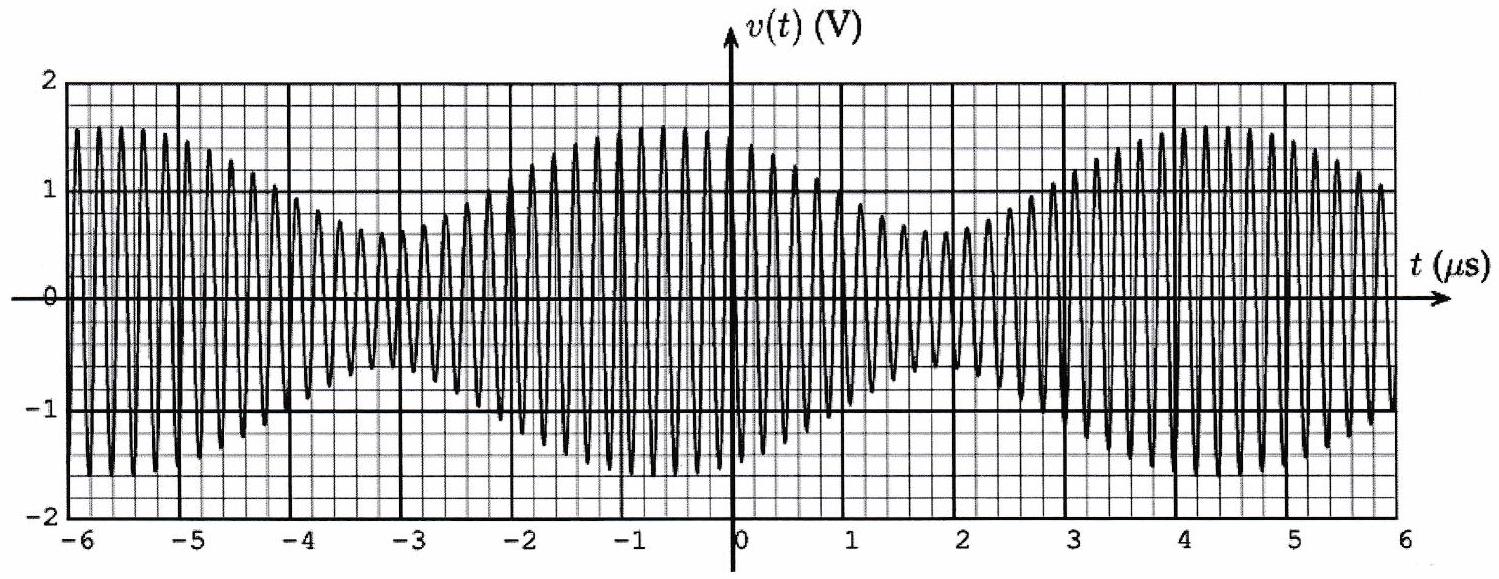
Un étudiant patient compte le nombre de fois où le signal coupe l’axe des abscisses sur le graphique ci-dessus et trouve 120. Quelles sont les fréquences des signaux originaux ? Leur amplitude? Tracer le spectre en amplitude de $v$.

Exercice 5 : Cuve à ondes - ★¶

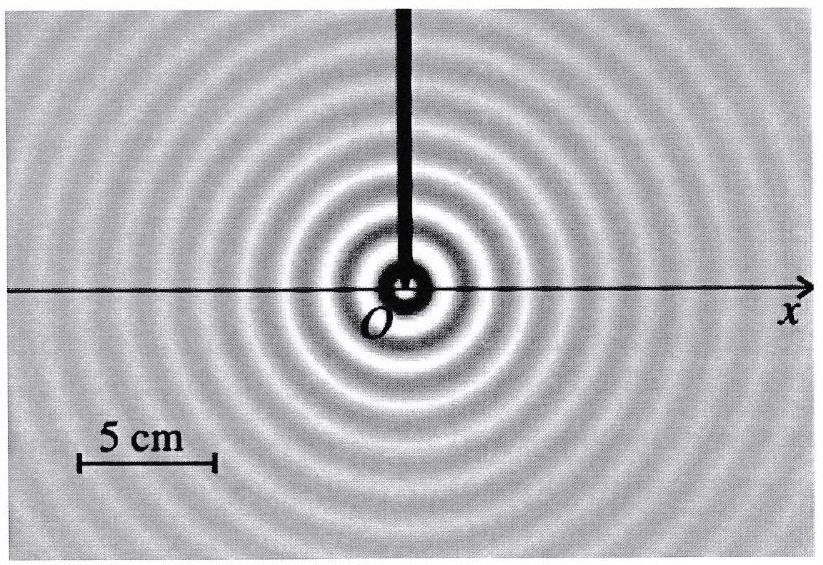
La figure représente la surface d’une cuve à onde éclairée en éclairage stroboscopique. L’onde est engendrée par un vibreur de fréquence $f=18 \mathrm{~Hz}$. Les zones sombres correspondent aux points “en creux”, et les zones les plus lumineuses aux points les plus élevés.

1. Mesurer la longueur d’onde.

2. En déduire la célérité de l’onde.

On suppose l’onde sinusoïdale, d’amplitude $A$ constante et de phase initiale nulle en $O$.

3. Écrire le signal $s(x, t)$ pour $x>0$ et pour $x<0$.

4. Expliquer qualitativement, pourquoi l’amplitude $A$ de l’onde n’est, en fait, pas constante.

Exercice 6 : Position et date d’un séisme - ★¶

Un séisme produit deux types d’ondes sismiques : les ondes P , longitudinales, qui se propagent avec la célérité $c_{P}$ et les ondes S , transversales, qui se propagent avec la célérité $c_{S}<c_{P}$.

1. Lors d’un séisme, on commence à détecter les premières à la date $t_{P}$ et les secondes à la date $t_{S}$. Montrer qu’on peut en déduire, connaissant $c_{S}$ et $c_{P}$, la distance $\Delta$ entre le foyer du séisme et l’appareil, ainsi que la date $t_{0}$ du début du séisme.

2. Pour un séisme, on mesure les distances $\Delta_{1}, \Delta_{2}$ et $\Delta_{3}$ entre le foyer du séisme et trois stations de mesure. Sans faire de calcul, montrer que cette information permet de localiser la position du foyer du séisme. Quel système fonctionne sur le même principe ?

Exercice 7 : Effet Doppler - ★★¶

Une ambulance, sirène allumée, passe dans la rue. La sirène émet des ondes sonores dont la célérité dans l’air est $c=340 \mathrm{~m} \cdot \mathrm{~s}^{-1}$. L’ambulance se déplace selon un axe ( $O x$ ) avec une vitesse $\overrightarrow{v_{0}}=v_{0} \overrightarrow{e_{x}}$ où $v_{0}>0$ et l’abscisse de l’ambulance est $x(t)>0$. Un piéton immobile situé en $x=0$ écoute l’ambulance s’éloigner.

1. On suppose dans un premier temps que la sirène de l’ambulance émet des bips tous les $T$. Déterminer l’expression de la période $T^{\prime}$ des bips reçus par le piéton en $x=0$.

2. À l’aide d’un développement limité au premier ordre en $v_{0} / c$, montrer que la fréquence $f^{\prime}$ des bips reçus par le piéton s’écrit :

3. La sirène émet maintenant un signal sinusoïdal de fréquence $f=1,00 \mathrm{kHz}$, calculer la fréquence $f^{\prime}$ du son entendu par le piéton si l’ambulance roule à $50 \mathrm{~km} \cdot \mathrm{~h}^{-1}$. Le son parait-il plus grave ou plus aigu que celui émis par la sirène ?

4. Comment est modifiée l’expression obtenue à la question 2 si le piéton avance à la vitesse $v_{p}$ constante en direction de l’ambulance qui s’éloigne ?

5. Dans le cas où l’ambulance se rapproche à $50 \mathrm{~km} \cdot \mathrm{~h}^{-1}$ du piéton immobile en $x=0$, calculer la fréquence $f^{\prime}$ du son entendu par le piéton ? Le son paraît-il plus grave ou plus aigu que celui émis par la sirène ?

L’effet Doppler est utilisé en astrophysique pour mesurer la vitesse radiale des galaxies par rapport à la Terre. Pour cela, le spectre de la lumière provenant de la galaxie est comparé au spectre des éléments sur Terre. Par exemple, pour la galaxie NGC 691, la longueur d’onde de la raie rouge de l’hydrogène, mesurée par décomposition de la lumière provenant de la galaxie, est $\lambda_{G}=661,5 \mathrm{~nm}$ alors que cette même raie mesurée sur Terre avec une lampe à hydrogène présente une longueur d’onde $\lambda_{0}=656 \mathrm{~nm}$. 6. Déterminer la vitesse de la galaxie par rapport à la Terre.

Exercice 8 : Principe de la télémétrie - ★★¶

On place un émetteur et un récepteur à ultrasons côte à côte. Ce bloc est appelé télémètre. À la distance $D$, on place un obstacle réfléchissant les ondes sonores, que nous appellerons la cible. Une onde sinusoïdale, de période $T$, est émise par l’émetteur du télémètre, elle se réfléchit sur la cible et est détectée par le récepteur du télémètre. Sur l’écran d’un oscilloscope, on visualise simultanément deux signaux : celui capté (par un dispositif non décrit) en sortie de l’émetteur et celui du récepteur.

1. On appelle temps de vol, noté $t_{v}$, la durée du trajet aller-retour de l’onde entre le télémètre et la cible. Exprimer $t_{v}$ en fonction de la distance $D$ séparant le télémètre de la cible et de la célérité de l’onde.

2. Pour illustrer le principe de la mesure, on colle la cible au télémètre, puis on l’éloigne lentement en comptant le nombre de coïncidences, c’est-à-dire le nombre de fois où les signaux sont en phase. Pour simplifier, on suppose que lorsque $D=0$, les signaux sont en phase. On se place dans le cas où l’on a compté exactement un nombre $n$ de coïncidences. Exprimer $D$ en fonction de $n$ et de la longueur d’onde des ondes ultrasonores.

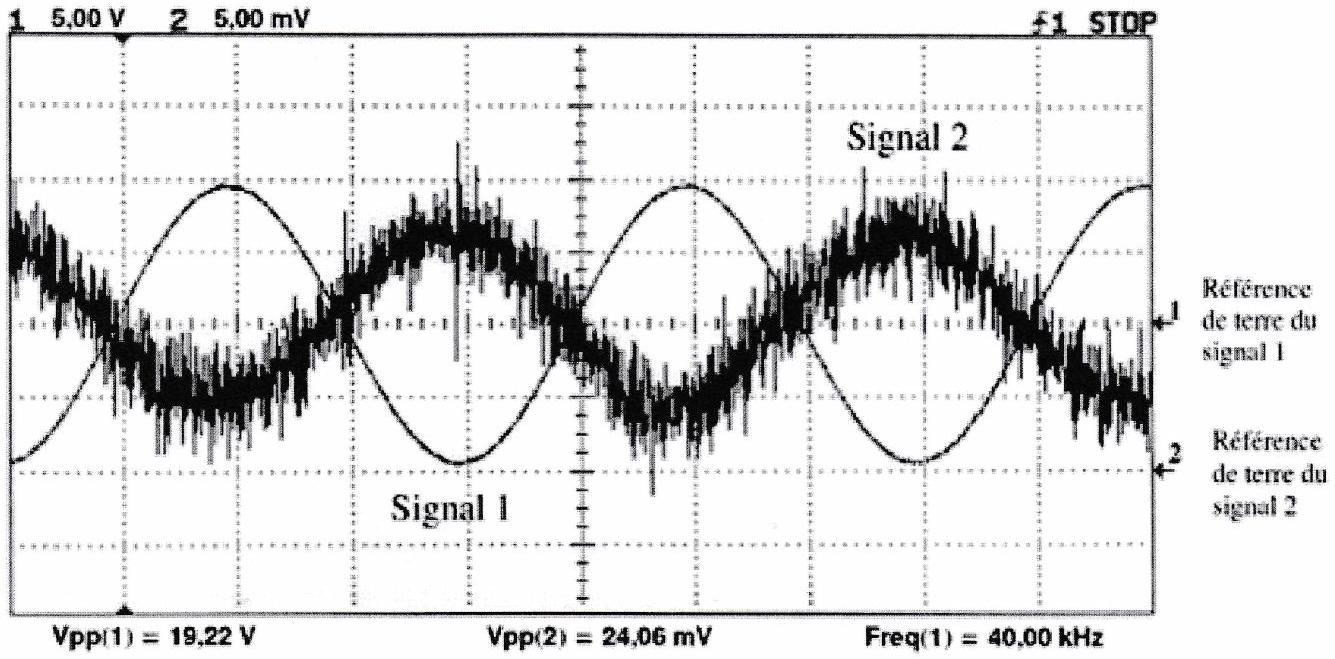
3. Lors du recul de la cible, 50 coïncidences ont été comptées avant d’observer les signaux de la figure sur l’oscilloscope. Dans les conditions de l’expérience, la longueur d’onde des ondes sonores valait $8,5 \mathrm{~mm}$. En exploitant les données de l’enregistrement, calculer la distance séparant le télémètre de la cible.

4. Pourquoi les signaux de la figure sont-ils si différents ? Identifier quel est, selon toute vraisemblance, le signal capté en sortie de l’émetteur et celui reçu par le récepteur.

5. Le comptage des coïncidences a été réalisé en plaçant l’oscilloscope en mode XY. Dans le cas des signaux de la figure, représenter la courbe que l’on obtiendrait en se plaçant dans ce mode.

Exercice 9 : La marée - ★★★¶

On appelle marée la variation temporelle du niveau des mers et des océans terrestres due à l’interaction gravitationnelle entre la terre, la Lune et le Soleil. La marée est un phénomène complexe dont la modélisation nécessite une connaissance précise des paramètres orbitaux du système Terre-Lune-Soleil mais aussi des caractéristiques géométriques des bassins océaniques et maritimes. Le but de cet exercice est d’étudier quelques caractéristiques de la marée dans le port de Brest à partir d’un enregistrement de la hauteur d’eau $h(t)$ en fonction du temps pour le mois de mai 2015 et de son spectre en amplitude.

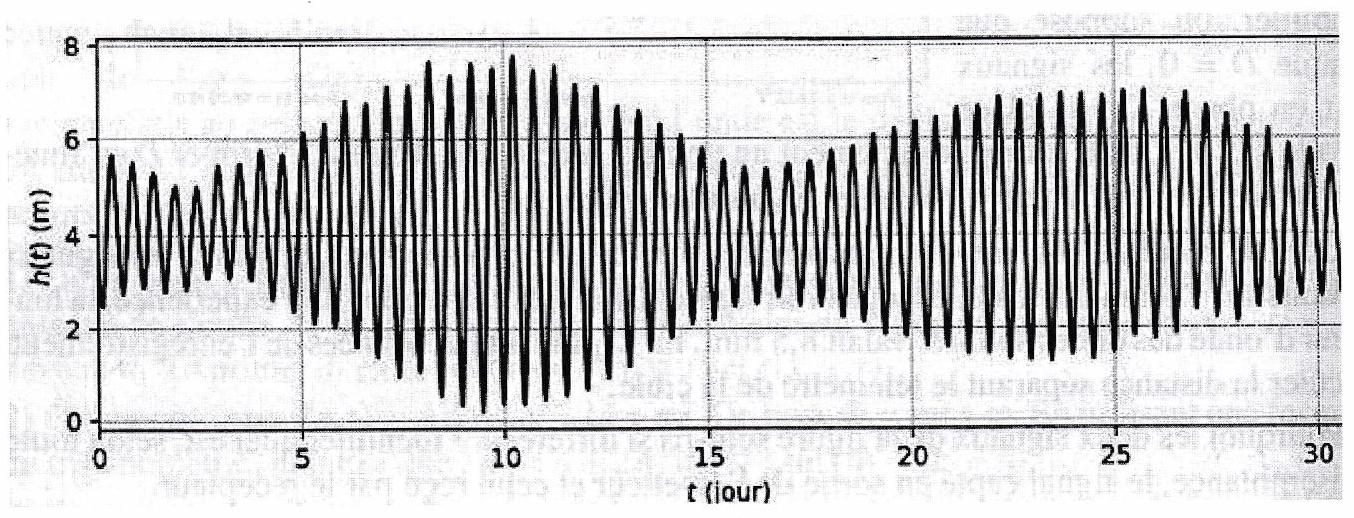
Figure 11.1: Hauteur de l’eau dans le port de Brest mesurée entre le 1er et le 31 mai 2015

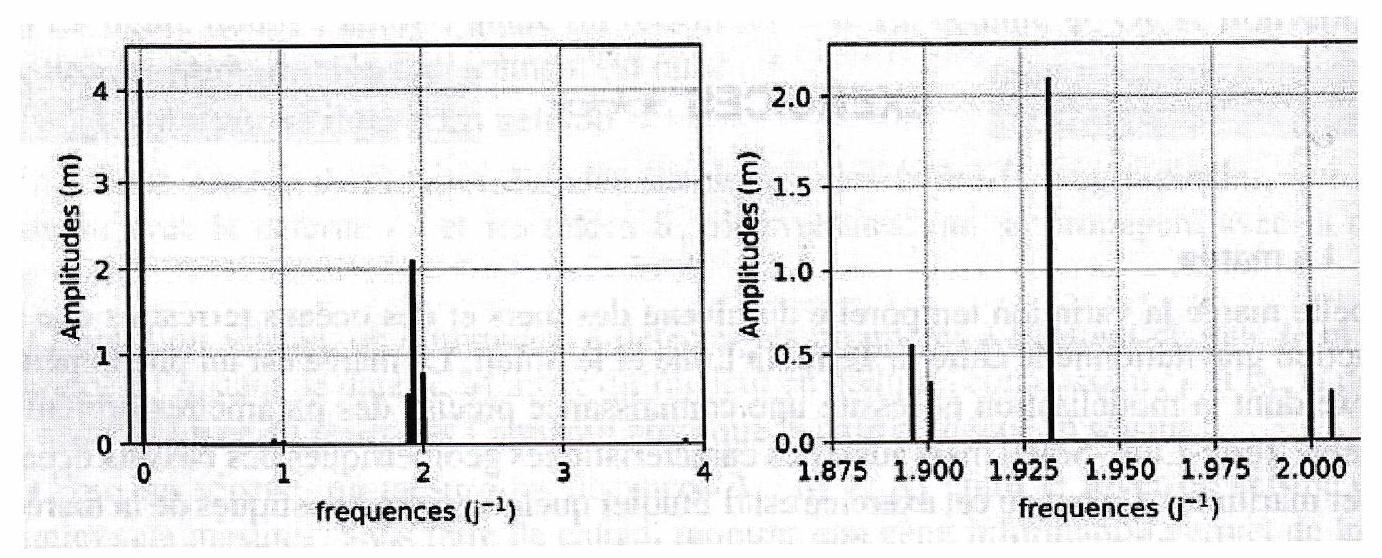
Figure 11.2: Spectrogramme d’amplitude de la marée de Brest calculé à partir du signal de la figure 11.1. La figure de droite est un zoom sur la partie centrale du spectre.

1. Quelle est la valeur moyenne de la hauteur d’eau dans le port de Brest ? Le signal est-il périodique?

2. Quelle est la durée moyenne entre deux marées hautes successives et la durée moyenne entre deux marées basses successives ? Ce résultat était-il prévisible à partir du spectre du signal ?

3. On observe des périodes dites de vives eaux, où l’écart entre une marée haute et une marée basse successives est maximal, et des périodes dites de mortes eaux où l’écart entre une marée haute et une marée basse successives est minimal. Quelle est la durée entre deux vives eaux successives ? entre deux mortes eaux ?

4. On modélise la variation de la hauteur d’eau en ne retenant que la composante continue et les deux composantes sinusoïdales les plus importantes, soit :

Donner les valeurs de $\omega_{1}$ et $\omega_{2}$. Préciser la période des deux composantes sinusoïdales. 5. Ce modèle permet-il d’expliquer l’alternance de vives eaux et de mortes eaux ?

Exercice 10 : Mesure du coefficient de tension superficielle de l’eau - ★★★¶

Une cuve à onde est un dispositif permettant de générer des ondes à la surface d’une mince couche et de projeter leur image sur un écran. Un vibreur dont on contrôle la fréquence percute la surface de l’eau et crée une onde approximativement sinusoïdale qui se propage dans toutes les directions. La gamme de longueurs d’onde accessibles varie typiquement entre 5 mm et 5 cm . Un dispositif d’éclairage stroboscopique permet de figer la propagation de l’onde et de mesurer la longueur d’onde. Pour ces longueurs d’onde, les forces intermoléculaires à l’interface entre l’eau et l’air ne sont pas négligeables. On parle d’ondes de capillarité, dont la relation de dispersion est :

avec $\gamma$ le coefficient de tension superficielle en $\mathrm{N} \cdot \mathrm{m}^{-1}$ et $\rho$ la masse volumique de l’eau. On donne $\rho=1,00 \cdot 10^{3} \mathrm{~kg} \cdot \mathrm{~m}^{-3}$. On consigne les longueurs d’onde $\lambda$ mesurées expérimentalement pour différentes fréquences $f$.

1. Montrer que la grandeur $l_{c}=\sqrt{\frac{\gamma}{\rho g}}$, appelée longueur capillaire, est bien homogène à une longueur.

2. À quelle condition sur la longueur d’onde peut-on négliger les forces intermoléculaires devant la gravité ? Cette condition est-elle remplie dans la cuve à onde ?

3. Montrer qu’à partir des données expérimentales on peut mesurer le coefficient de tension superficielle de l’eau.