Chapitre 10¶

Amplificateur linéaire intégré¶

I ) Filtres actifs¶

A) Définitions¶

Définition 1 : Filtres passifs et actifs¶

Un filtre passif est un filtre qui ne dispose pas de source d’énergie extérieure. C’est le cas des filtres constitués uniquement de résistances, condensateurs, bobines, étudiés dans le chapitre précédent. À l’inverse, un filtre actif dispose d’une source d’énergie extérieure, et c’est le cas par exemple s’il contient un amplificateur linéaire intégré.

B) Présentation de l’amplificateur linéaire intégré (ALI)¶

Un amplificateur linéaire intégré, plus connu sous le nom d’amplificateur opérationnel, dont les acronymes sont ALI et AO, se présente sous la forme d’une puce électronique, représentée ci-contre. Elle comporte huit pattes et une encoche semi-circulaire permettant de les dis-

tinguer.

Chaque patte de l’amplificateur linéaire intégré a un rôle bien particulier. Dans l’ordre de numérotation du constructeur (avec l’encoche semi-circulaire vers le haut) :

1. offset permet de compenser les petits défauts de tension, dus à la construction. Il ne sera pas utilisé dans ce cours ;

2. entrée inverseuse repérée sur les schémas par le signe $\ominus$;

3. entrée non inverseuse repérée par le signe ⊕ ;

4. alimentation négative de la puce, en général -15 V ;

5. offset est identique à la patte 1 ;

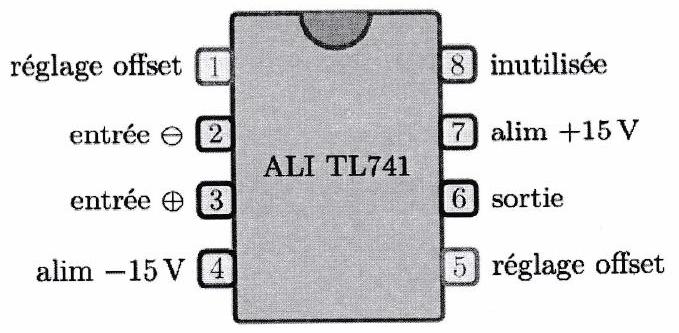
6. sortie ;

7. alimentation positive de la puce, en général +15 V ;

8. non connectée, cette patte est inutilisée.

Un amplificateur opérationnel, comme toutes les puces électroniques, doit être alimenté pour fonctionner, puisqu’il s’agit d’un composant actif.

Un amplificateur opérationnel doit être alimenté en -15 V et +15 V . (8) $\begin{aligned} & \text { L'alimentation de l'amplificateur linéaire intégré est la première chose à brancher } \\ & \text { (et la dernière à débrancher) sur un montage électronique, avant les signaux } \\ & \text { d'entrée. }\end{aligned}$

L’alimentation n’est toutefois pas représentée sur les schémas électriques, qui symbolisent l’amplificateur linéaire intégré par un triangle ou un rectangle, avec deux entrées et une sortie.

Représentation conventionnelle de l’amplificateur linéaire intégré

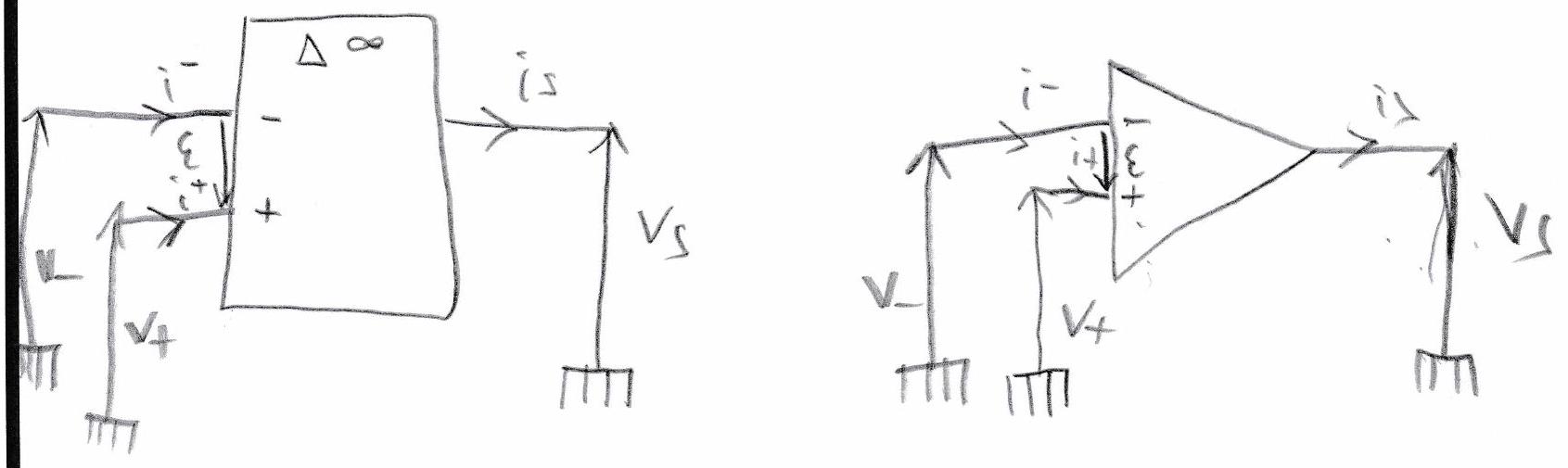
L’amplificateur linéaire intégré a deux entrées : l’entrée inverseuse ( - ), de potentiel $V^{-}$et l’entrée non inverseuse ( + ), de potentiel $V^{+}$. On définit la tension différentielle en entrée par : $\varepsilon=V^{+}-V^{-}$. Les courants entrants $i^{-}$et $i^{+}$sont appelés courants de polarisation et sont très faibles. L’amplificateur linéaire intégré a une sortie, dont on note le potentiel $V_{s}$.

Remarque¶

Un amplificateur linéaire intégré est un circuit intégré, c’est-à-dire qu’il contient d’autres composants élémentaires. Nous l’étudierons en “boîte noire”, sans faire référence à sa constitution interne.

II ) Comportement de l’amplificateur linéaire intégré¶

A) Régime linéaire et de saturation¶

On représente ci-dessous la caractéristique statique de l’amplificateur linéaire intégré qui représente la tension de sortie $V_{s}$ en fonction de la tension différentielle d’entrée $\varepsilon=V^{+}-V^{-}$ en régime permanent continu.

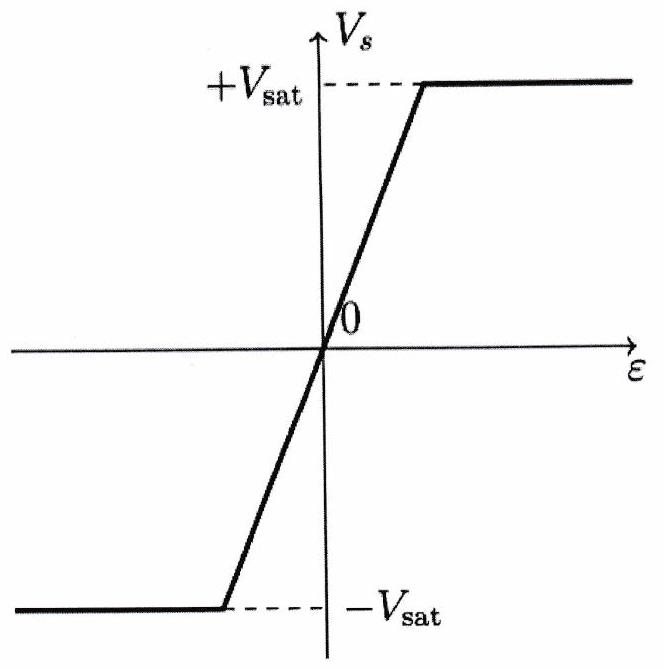
La tension de sortie $V_{s}$ ne peut pas sortir de l’intervalle $\left[-V_{\text {sat }},+V_{\text {sat }}\right]$, où $V_{\text {sat }}=15 \mathrm{~V}$. On distingue deux régimes :

• Si $-V_{\text {sat }}<V_{s}<+V_{\text {sat }}$ : régime linéaire, la tension de sortie du montage est reliée à la tension différentielle d’entrée par une relation linéaire.

• Si $V_{s}= \pm V_{\text {sat }}$ : régime de saturation, $V_{s}$ n’évolue plus même si $\varepsilon$ évolue, la relation entrée-sortie n’est plus linéaire.

B ) Modèle de l’ALI idéal¶

Modèle de l’ALI idéal¶

• Les courants d’entrée $i^{+}$et $i^{-}$sont nuls. L’impédance d’entrée de l’ALI est donc infinie.

• L’impédance de sortie de l’ALI est nulle. Le courant de sortie $i_{s}$ et le potentiel de sortie $V_{s}$ sont donc indépendants.

C) Fonctionnement linéaire¶

On appelle boucle de rétroaction ou chaîne de retour un dispositif par lequel le signal de sortie d’un système affecte le signal d’entrée. Le système est alors dit bouclé. Ici, cela consiste à relier la borne de sortie de l’ALI par un dipôle ou une association de dipôles à l’une ou l’autre des bornes d’entrée. La rétroaction est dite négative si elle se fait sur l’entrée $\ominus$ et positive si elle a lieu sur l’entrée $\oplus$.

• Aucune rétroaction : régime de saturation

• Une unique rétroaction négative : régime linéaire (si tension d’entrée pas trop grande)

• Une unique rétroaction positive : régime de saturation

• Deux rétroactions $\oplus$ et $\ominus$ : impossible de savoir a priori

ALI idéal en régime linéaire¶

Pour un ALI idéal fonctionnant en régime linéaire, la tension différentielle en entrée est nulle :

Dans la suite du cours et des exercices, tous les ALI seront supposés idéaux et fonctionnant en régime linéaire.

III ) Exemples de montages¶

Dans cette partie, nous allons étudier différents montages de base. Les méthodes mises en œuvre ici seront adaptées à d’autres montages en TD.

A) Méthodes¶

Méthode : Comment établir la relation entrée-sortie?¶

• Représenter le circuit et définir une tension aux bornes de chaque dipôle et une intensité à travers chaque dipôle.

• Utiliser le fait que les courants d’entrée $i^{+}$et $i^{-}$sont nuls pour un ALI idéal.

• Écrire que pour un ALI idéal en régime linéaire : $V^{-}=V^{+}$

• Il faut ensuite exprimer $V^{+}$et $V^{-}$en fonction de $V_{s}$ et $V_{e}$. Pour cela :

• Voir si l’on peut simplement remplacer $V^{+}$et/ou $V^{-}$par $V_{e}$, par $V_{s}$, ou par 0 V .

• OU Écrire un pont diviseur de tension sur les entrées ⊕ ou • (possible car les courants de polarisation sont nuls).

• OU Écrire la loi des nœuds et les relations courant/tension des différents dipôles (loi des noeuds en terme de potentiels).

• Utiliser ces relations dans $V^{-}=V^{+}$.

• Manipuler les relations pour obtenir l’expression de $V_{s}$ en fonction de $V_{e}$.

Méthode : Comment déterminer l’impédance d’entrée d’un montage?¶

• Exprimer la relation entre la tension $V_{e}$ en entrée du montage, et le courant d’intensité $i_{e}$ entrant dans le montage.

• Si besoin, utiliser $V^{-}=V^{+}$pour un ALI idéal en régime linéaire.

• Conclure en utilisant la définition de l’impédance d’entrée : $\underline{Z_{e}}=\frac{\underline{V_{e}}}{\underline{i_{e}}}$

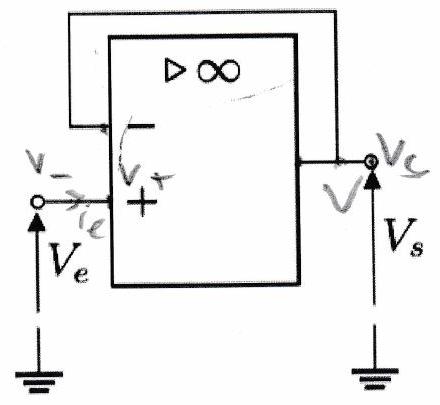
B ) Montage suiveur¶

Exercice de cours à connaître 1¶

1. Exprimer le potentiel $V^{-}$de l’entrée inverseuse.

2. Exprimer de même le potentiel $V^{+}$de l’entrée non inverseuse.

3. En utilisant le modèle de l’ALI idéal en fonctionnement linéaire, relier $V^{+}$à $V^{-}$. En déduire la relation entre $V_{s}$ et $V_{e}$.

4. Justifier le nom de “montage suiveur”.

5. Que vaut $i_{e}$ le courant d’entrée entrant par l’entrée non inverseuse?

6. Quelle est l’impédance d’entrée de ce montage ?

7. Quelle est l’impédance de sortie de l’ALI idéal?

8. En déduire l’intérêt du montage suiveur.

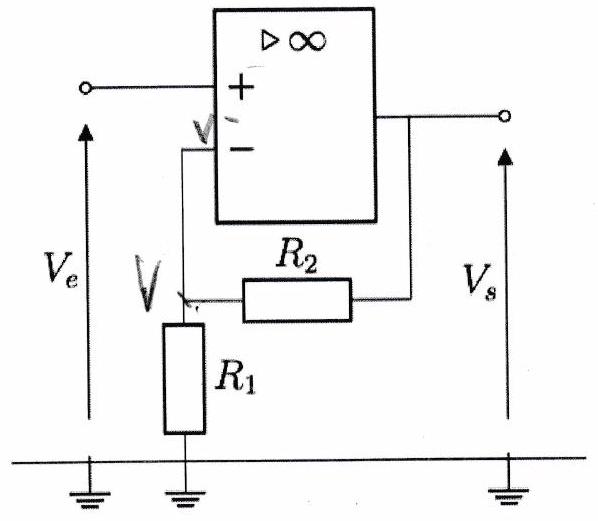
C ) Montage amplificateur non inverseur¶

Exercice de cours à connaître 2¶

1. Que vaut le courant $i^{-}$? Que peut-on dire des deux résistances $R_{1}$ et $R_{2}$ ?

2. Exprimer le potentiel $V^{-}$de l’entrée inverseuse.

3. En utilisant le modèle de l’ALI idéal en fonctionnement linéaire, relier $V^{+}$à $V^{-}$. En déduire la relation entre $V_{s}$ et $V_{e}$.

4. Justifier le nom de “montage amplificateur non inverseur”.

5. Que vaut $i_{e}$ le courant d’entrée entrant par l’entrée non inverseuse?

6. En déduire l’impédance d’entrée du montage amplificateur non inverseur.

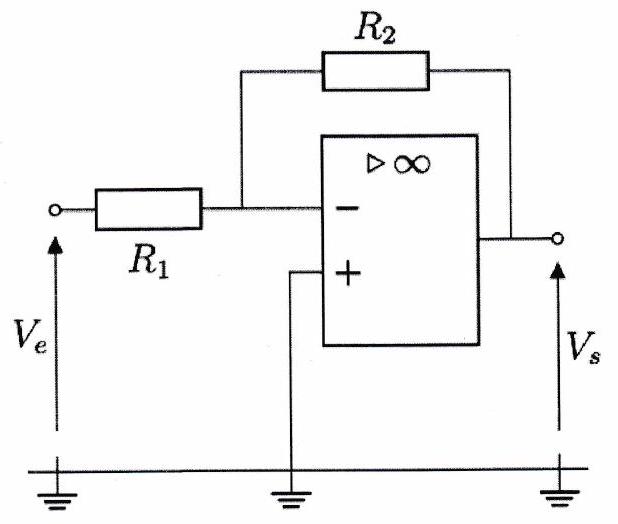
D ) Montage amplificateur inverseur¶

Exercice de cours à connaître 3¶

1. Que vaut le courant $i^{-}$? Que peut-on dire des deux résistances $R_{1}$ et $R_{2}$ ?

2. Établir une relation entre $V_{e}, V^{-}, V_{s}$ et les résistances.

3. En utilisant le modèle de l’ALI idéal en fonctionnement linéaire, relier $V^{+}$à $V^{-}$. En déduire la relation entre $V_{s}$ et $V_{e}$.

4. À quelle condition ce montage réalise-t-il une amplification ?

5. Exprimer l’intensité $i_{e}$ du courant entrant dans le montage et qui traverse la résistance $R_{1}$.

6. En déduire l’expression de l’impédance d’entrée de ce montage.

7. Quel problème cela peut-il poser?

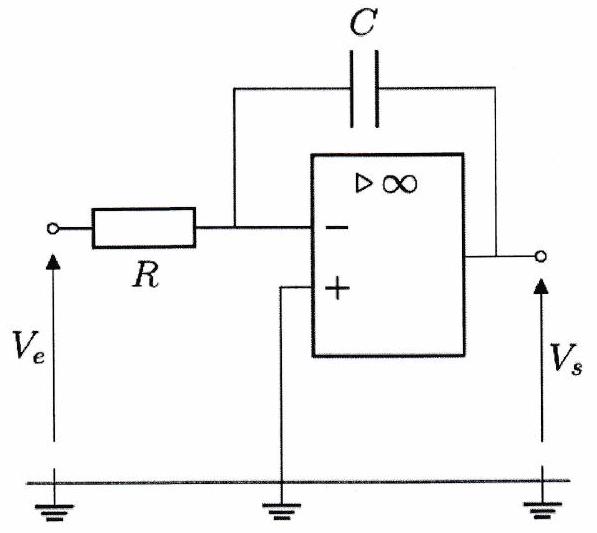
E ) Montage intégrateur¶

Exercice de cours à connaître 4¶

Supposons que $V_{e}$ est sinusoïdal de pulsation $\omega$, et utilisons la représentation complexe.

1. Établir l’expression de $\underline{V_{s}}$ en fonction de $\underline{V_{e}}, R$, $C$, et $j \omega$.

2. Repasser en réel pour obtenir l’expression de $V_{s}$ en fonction de $V_{e}$.

3. Déterminer l’expression de l’impédance d’entrée de ce montage.

4. Quel problème cela peut-il poser?