Chapitre 9
Chapitre 9¶
Modèles de filtres passifs¶
Dans le chapitre précédent, nous avons étudié les principes du filtrage linéaire en électrocinétique ainsi que le formalisme à travers un exemple : le filtre passe-bas du premier ordre. Nous avons ainsi pu voir l’utilité d’un filtre passe-bas à travers les différentes opérations qu’il peut réaliser sur un signal périodique (moyennage, réduction du bruit haute fréquence et intégration d’un signal). Dans ce chapitre, nous mettrons en application tout ce que nous avons vu dans le chapitre précédent afin d’étudier d’autres modèles de filtres passifs (passe haut, passe bande) ainsi que leur utilité pour filtrer un signal périodique. Nous verrons enfin les précautions qu’il faut prendre lorsque qu’une charge est branchée en sortie du filtre.
I) Filtre passe-haut du premier ordre¶
A ) Exemple de montage¶
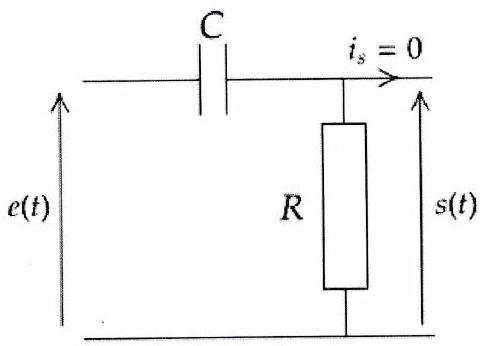
Figure 9.1: Circuit série : sortie aux bornes de
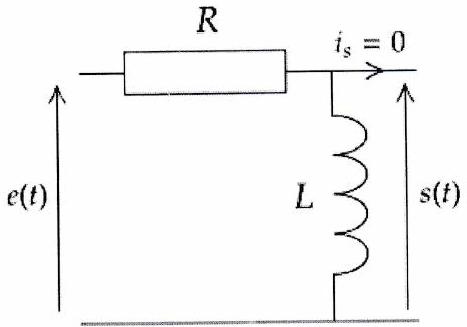
Figure 9.2: Circuit série : sortie aux bornes de
B) Fonction de transfert et diagramme de Bode¶
Exercice de cours à connaître 1¶
On considère les deux montages précédents en sortie ouverte, donc . Ils sont tous deux alimentés par une tension sinusoïdale de la forme .
Démontrer par un étude asymptotique du circuit que ces deux montages permettent la réalisation d’un filtrage passe-haut.
Déterminer pour les deux montages la fonction de transfert , la mettre sous forme canonique :
Vous exprimerez et en fonction des paramètres du circuit. 3. À partir de la forme canonique, déterminer la pulsation de coupure du filtre et en déduire la bande passante à -3 dB . 4. Réaliser le tracé du diagramme de Bode.
La fonction de transfert canonique d’un filtre passe-haut du 1er ordre se met sous la forme :
avec :
: Le gain asymptotique (pour ).
la pulsation réduite, correspond à une pulsation caractéristique du circuit et dans le cas du passe-haut d’ordre 1 , c’est aussi la pulsation de coupure à -3 dB : .
Diagramme de Bode d’un filtre passe-haut d’ordre 1
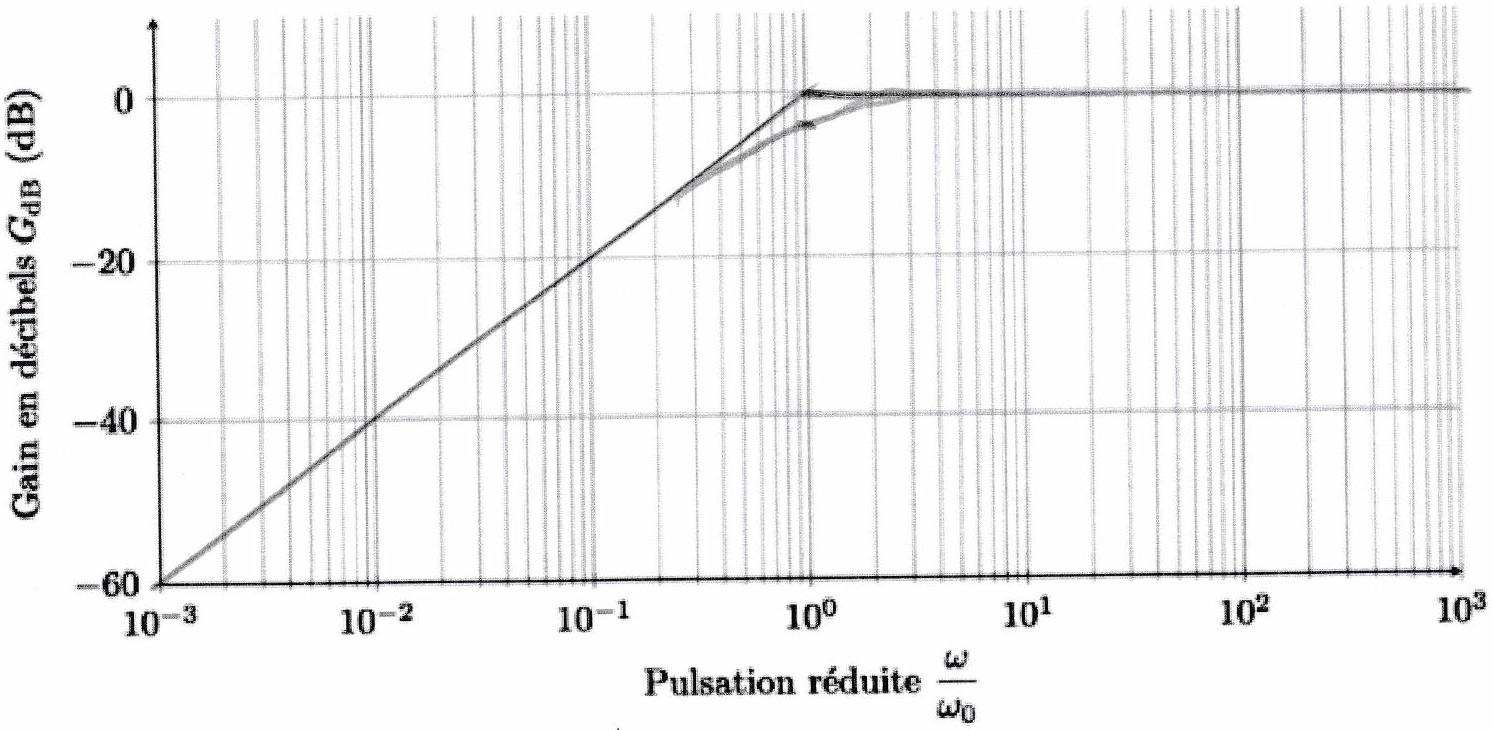
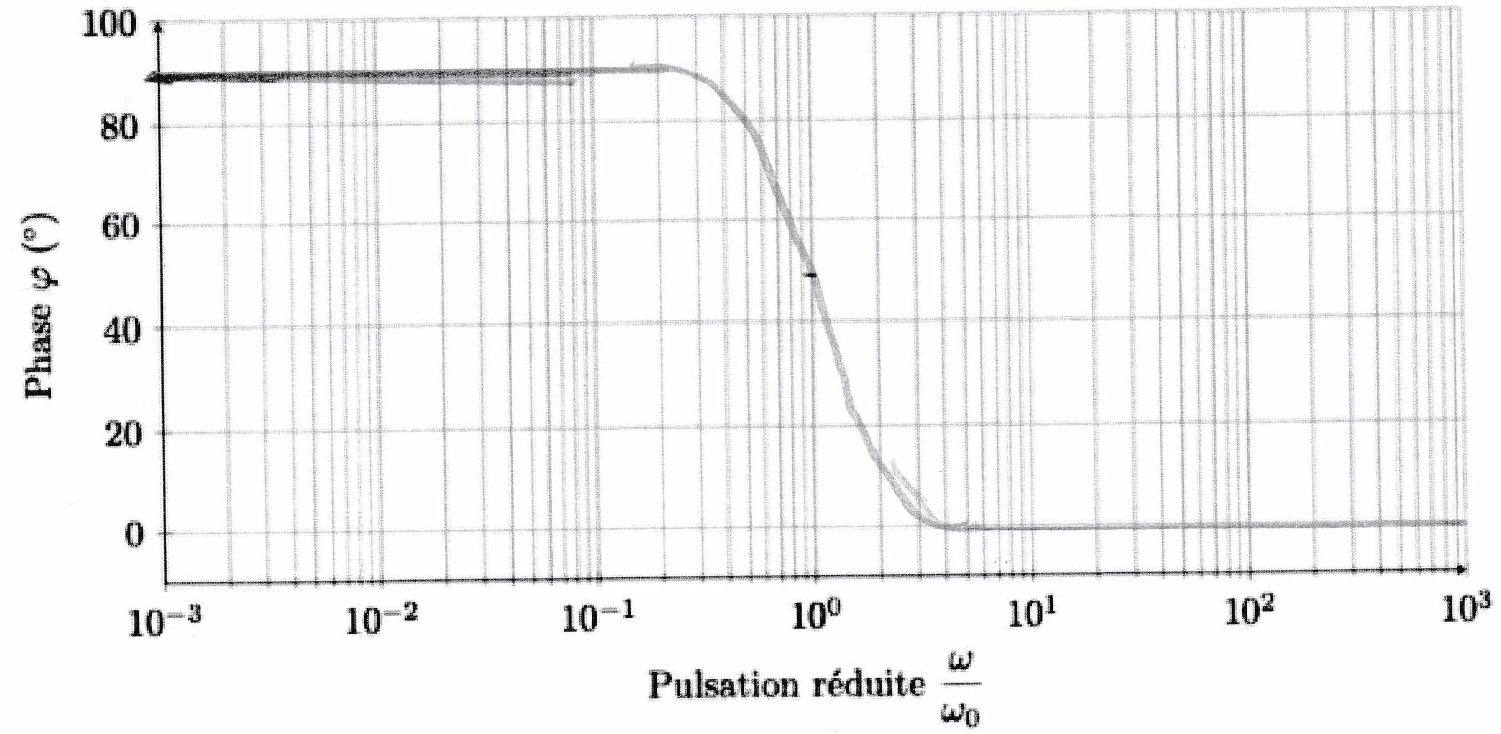
C ) Comportement pseudo-dérivateur à basse fréquence¶
Exercice de cours à connaître 2¶
Donner l’équivalent de la fonction de transfert à basse fréquence (quand ).
En repartant de la définition de la fonction de transfert harmonique, déterminer l’expression du signal de sortie en fonction du signal d’entrée. Quelle opération mathématique réalise un filtre passe-haut du 1er ordre sur un signal d’entrée de fréquence petite devant la fréquence de coupure?
Si un filtre possède dans une certaine gamme de fréquence de son diagramme de Bode, une asymptote de pente +20 dB /décade, alors il aura un comportement dérivateur sur cette gamme de fréquence.
Expérience 1 : Pseudo-dérivation d’un signal triangulaire¶
On observe la tension aux bornes du résistor d’un filtre . Il s’agit alors d’un filtre passe-haut du premier ordre, de fréquence de coupure . On alimente le circuit avec une tension triangulaire de fréquence
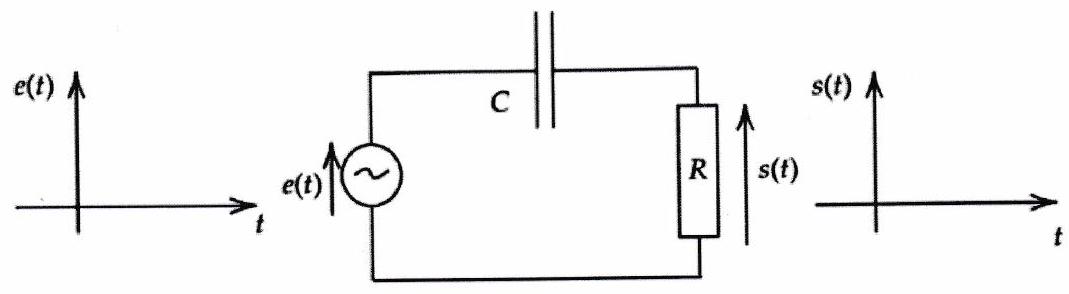
Quelle est la forme du signal obtenu ? Justifier la cohérence de la forme obtenue.
Remarque¶
On parle de comportement pseudo-dérivateur, car un comportement dérivateur n’est valable que si toutes les harmoniques du signal ont une fréquence . De plus, dans le cadre du filtre passe-haut, la dérivation ne se fait qu’au prix d’une forte atténuation du signal, on préféra utiliser un montage dérivateur qui n’affecte pas l’amplitude du signal en sortie (cf chapitre suivant).
D) Suppression de la composante continue d’un signal¶
Exercice de cours à connaître 3¶
On considère un filtre passe-haut d’ordre 1 dont la fonction de transfert s’écrit :
de pulsation de coupure et avec .
On envoie à l’entrée de ce filtre une tension avec .
Montrer que l’opération de filtrage a permis de supprimer la composante continue du signal sans atténuer l’amplitude du fondamental.
Comment choisir la pulsation de coupure pour que le fondamental soit transmis sans atténuation?
Le filtre passe-haut est donc capable de supprimer la composante continue (offset) du signal d’entrée. Pour récupérer le reste du signal sans atténuation, il suffit que le fondamental et les composantes harmoniques soient de fréquence .
Remarque¶
Ce résultat reste bien sûr valable pour un signal plus complexe comme le signal triangle, à condition que la fréquence fondamentale soit grande devant (si le fondamental et quelques harmoniques sont dans la zone d’atténuation du filtre, le signal sera déformé en sortie).
II ) Filtre passe-bas du deuxième ordre¶
A) Fonction de transfert et diagramme de Bode¶
On peut réaliser un filtre passe-bande d’ordre 2 , à l’aide d’un circuit , la sortie étant prise aux bornes du condensateur.
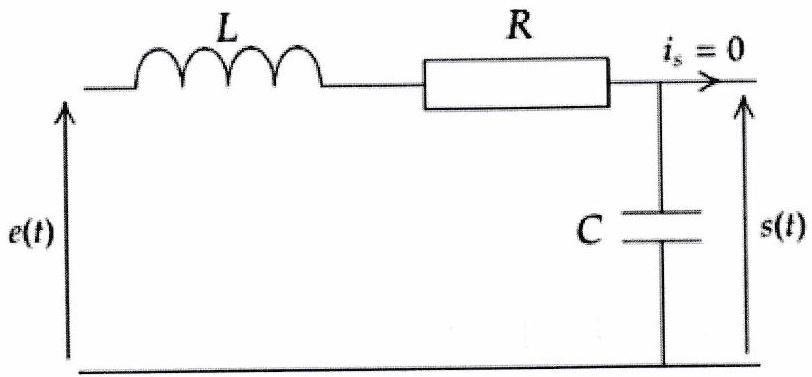
Exercice de cours à connaître 4¶
Démontrer à l’aide d’un étude asymptotique du circuit que le montage précédent permet de réaliser un filtre passe-bas.
Déterminer la fonction de transfert sous la forme :
On exprimera et en fonction des paramètres du circuit. 3. Calculer le gain du filtre et étudier la possibilité d’une résonance. Donner la condition sur pour que la résonance existe et exprimer la pulsation de résonance . 4. Réaliser une étude asymptotique de la fonction de transfert et compléter le tableau suivant :
| Basse fréquence | Haute fréquence | |
|---|---|---|
| 20 log (Howo) ) 40 log ( 10 ) | ||
| Pente en dB/décade | 0 | - 40 dB/diciade |
| Type de comportement | X | Double intergation |
| Déphasage | 0 |
Tracer le diagramme de Bode asymptotique de ce filtre :
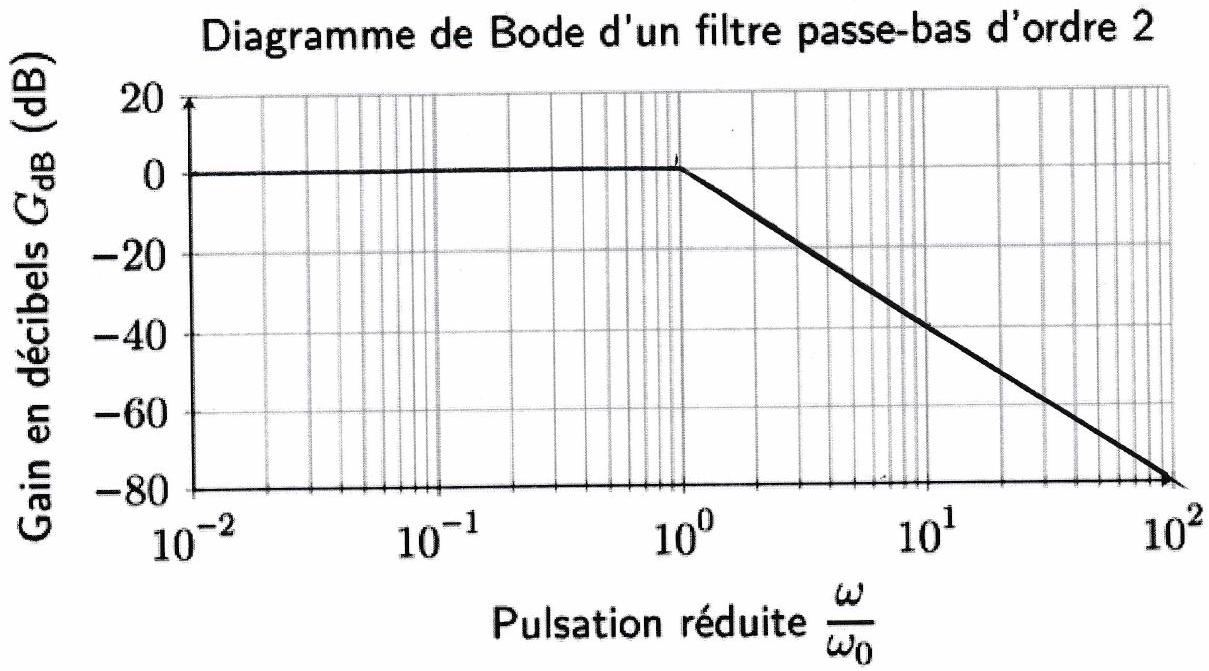
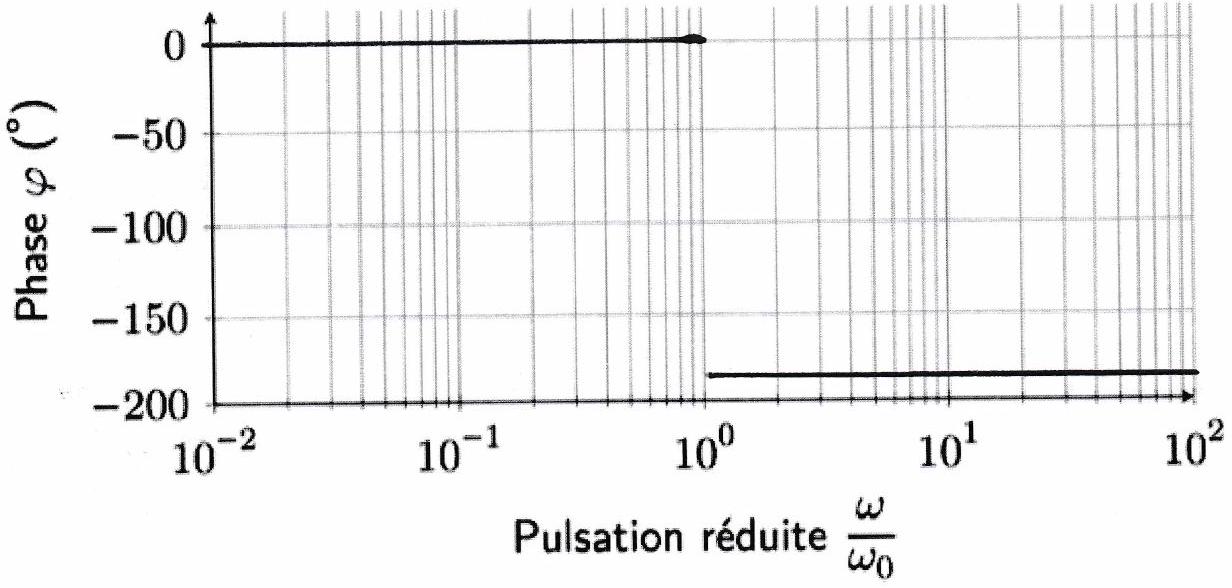
Diagramme de Bode réel¶
Pour un filtre passe-bas d’ordre 2 et différentes valeurs du facteur de qualité , le diagramme de Bode réel est le suivant :
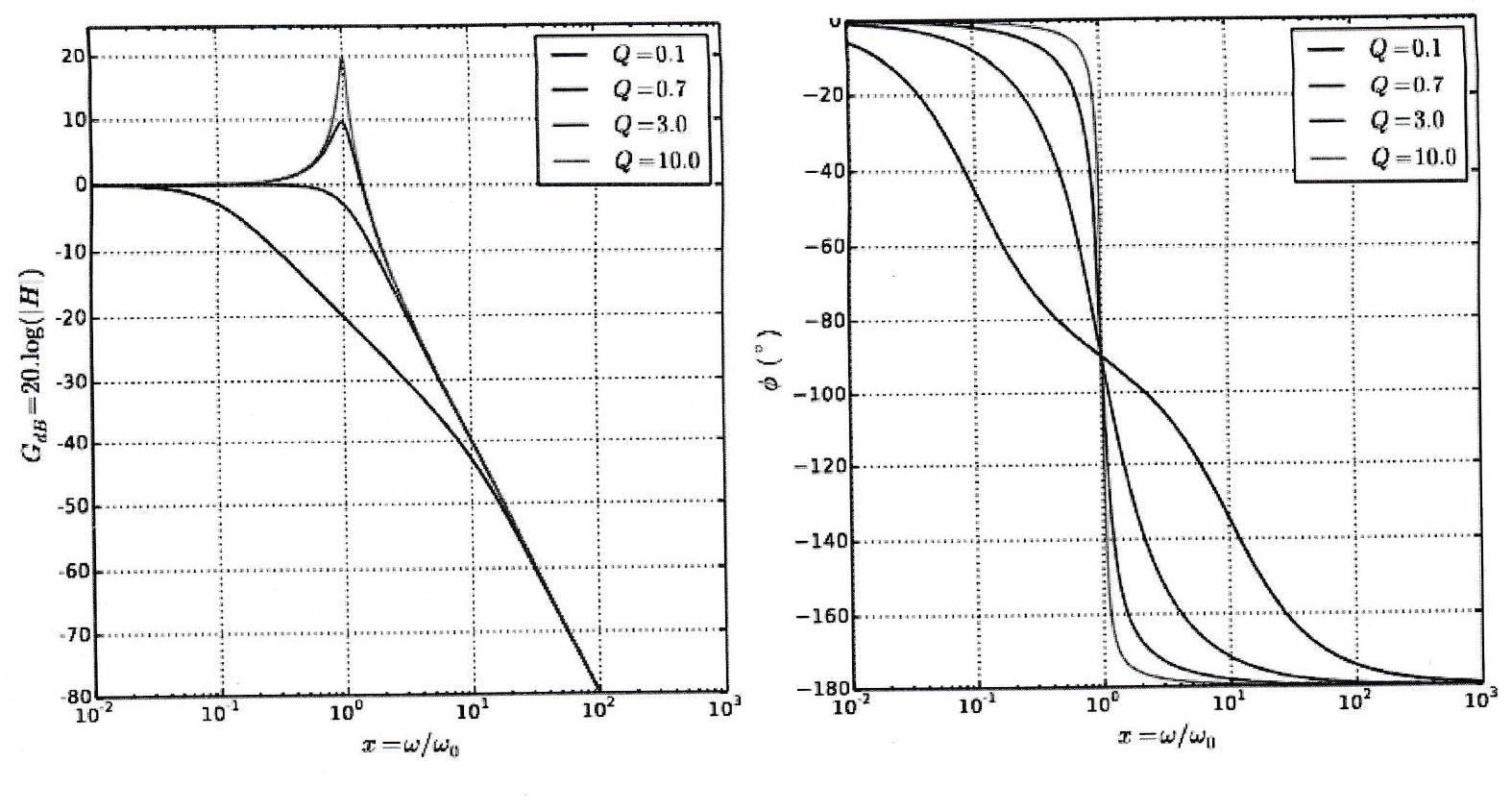
B ) Comparaison avec le filtre passe-bas d’ordre 1¶
Le diagramme de Bode d’un filtre passe-bas d’ordre 2 est caractérisé par une asymptote à haute fréquence dont la pente est de décade. Cela signifie qu’à chaque décade (multiplication de la fréquence par dix), l’amplitude du signal de sortie est divisée par cent : la coupure des hautes fréquences est beaucoup plus efficace qu’avec un filtre du premier ordre (pente de -20 dB /décade, donc seulement division par dix à chaque décade). L’inconvénient d’un filtre passe-bas du second ordre est qu’il peut être résonnant (si ) ce qui peut être problématique si l’on cherche seulement à atténuer les hautes fréquences. Ce n’est pas le cas pour un filtre d’ordre 1. On résume ces informations dans le tableau suivant :
| Pâsse-bas d’ordre 1 | Passe-bas d’ordre 2 | |
|---|---|---|
| Pente de l’asymptote à haute fréquence en dB/décade | -20 JB/decade | - cade |
| Déphasage | ||
| Résonance | X | omi |
III ) Filtre passe-bande du deuxième ordre¶
On peut réaliser un filtre passe-bande d’ordre 2 , à l’aide d’un circuit , la sortie étant prise cette fois-ci aux bornes de la résistance.
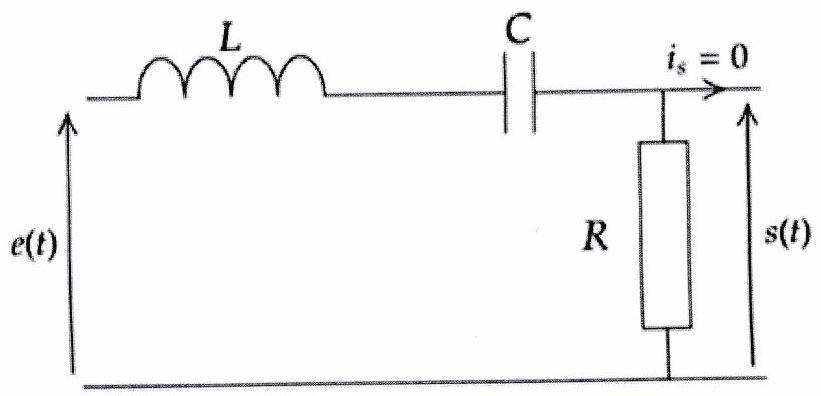
Exercice de cours à connaître 5¶
Démontrer à l’aide d’un étude asymptotique du circuit que le montage précédent permet de réaliser un filtre passe-bande.
Déterminer la fonction de transfert de ce filtre sous la forme :
On exprimera et en fonction des paramètres du circuit. 3. En déduire l’expression du gain de ce filtre. Pour quelle pulsation est-il maximal ? 4. Que valent le gain et le déphasage à la résonance ? 5. Déterminer les équations des asymptotes de la courbe de réponse en gain. Quel comportement cela traduit-il ? 6. Remplir le tableau suivant :
| Basse fréquence | Haute fréquence | |
|---|---|---|
| Pente en dB/décade |
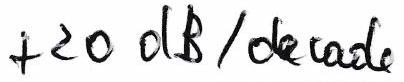
|
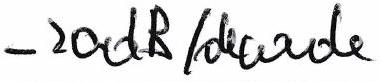
| | Type de comportement | dirivateur |

| | Déphasage | | |
Déterminer les coordonnées du point d’intersection des asymptotes. En déduire suivant la valeur de la position de la courbe réelle par rapport aux asymptotes.
Rappelez la relation entre la largeur de la bande passante à -3 dB , la pulsation de résonance et le facteur de qualité . Sur quel critère peut-on dire qu’un filtre passe-bande est sélectif ?
Les 3 grandeurs caractéristiques d’un filtre passe bande sont :
Son gain maximal c’est le gain à la résonance ;
sa pulsation de résonance ;
son facteur de qualité .
Toutes ces informations sont contenues dans la forme canonique de sa fonction de transfert :
Plus le facteur de qualité d’un filtre passe-bande est grand, plus ce dernier est dit sélectif.
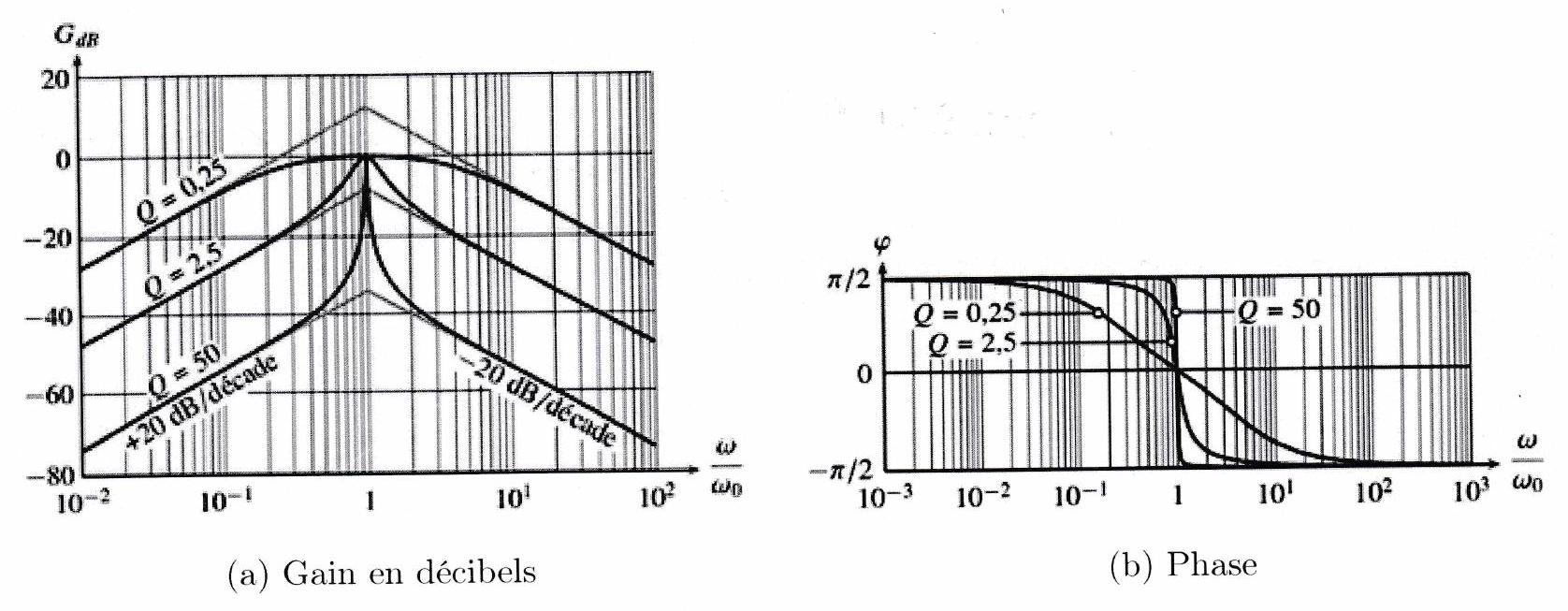
Figure 9.3: Diagramme de Bode d’un filtre passe-bande pour différentes valeurs de
Remarque¶
Il s’agit bien d’un filtre d’ordre 2, en effet la fonction de transfert peut aussi se mettre sous la forme :
IV ) Perturbation induite par la charge¶
Dans cette partie, nous nous intéresserons à l’influence de la présence d’une charge sur le comportement d’un filtre.
A) Mise en évidence¶
Nous souhaitons désormais connecter le filtre passe bas à une charge (moteur, appareil électronique, etc) que nous modélisons par une résistance branchée aux bornes de la capacité.
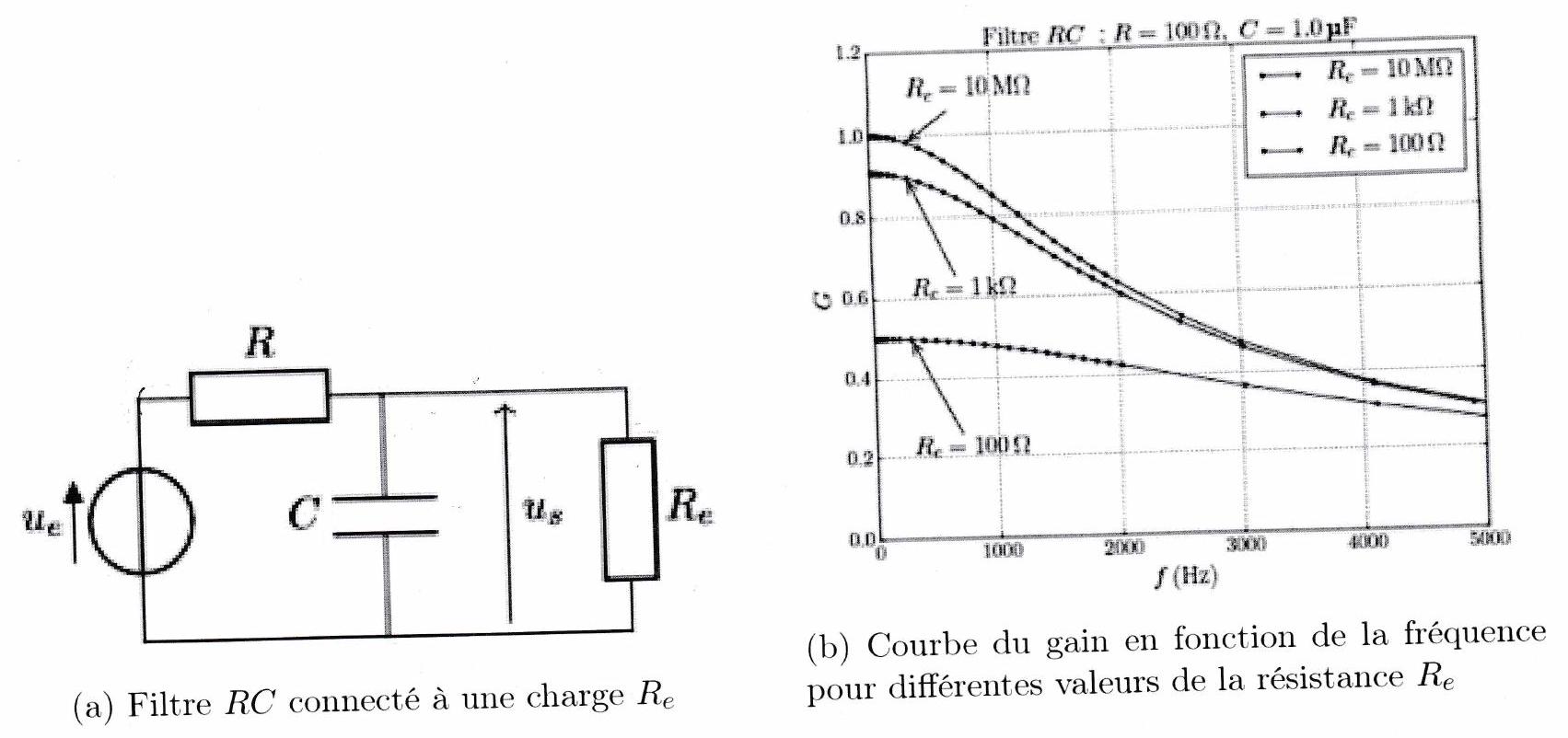
Figure 9.4: Perturbation induite par la présence d’une charge
Exercice de cours à connaître 6¶
Que peut-on dire du gain à basse fréquence lorsque la résistance de charge diminue?
Donner une explication qualitative à cette observation.
Montrer que la fonction de transfert de ce filtre avec charge s’écrit sous la forme :
On exprimera et en fonction des paramètres du circuit. 4. À quelle condition sur la résistance pouvons-nous retrouver l’expression de la fonction de transfert du filtre passe-bas d’ordre 1 en sortie ouverte? Interpréter.
B ) Impédances d’entrée et de sortie d’un filtre¶
Considérons un quadripôle avec en entrée une source de tension réelle, modélisée par un générateur de Thévenin, et en sortie une charge d’impédance .
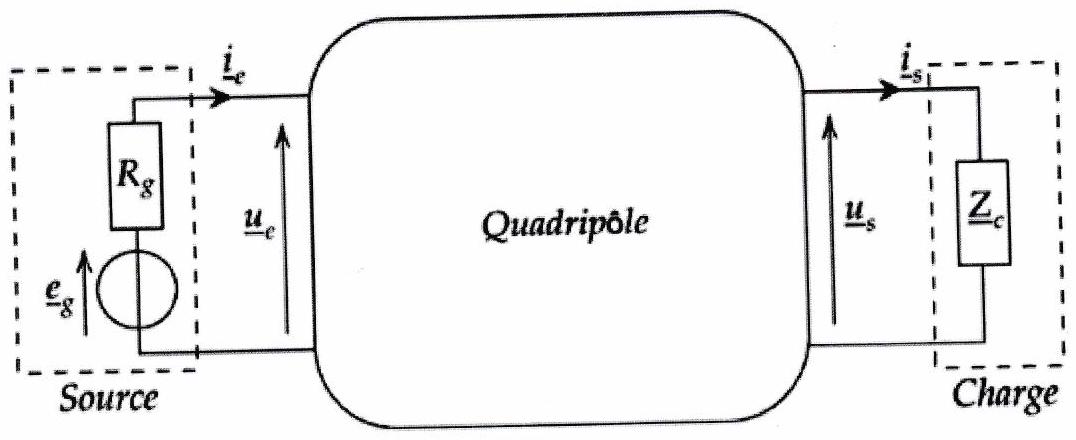
1 ) Impédance d’entrée¶
Lorsqu’une source est branchée sur un quadripôle, elle débite un courant d’entrée . Tous les composants du quadripôle étant linéaires, il est possible de modéliser l’ensemble du circuit situé après l’entrée du quadripôle, quadripôle et charge éventuelle, par une impédance , appelée impédance d’entrée, sur laquelle la source est branchée.
Définition 1 : Impédance d’entrée¶
Vu depuis l’entrée (donc depuis la source), le filtre et sa charge éventuelle se comportent comme une impédance , appelée impédance d’entrée du filtre, et définie par :
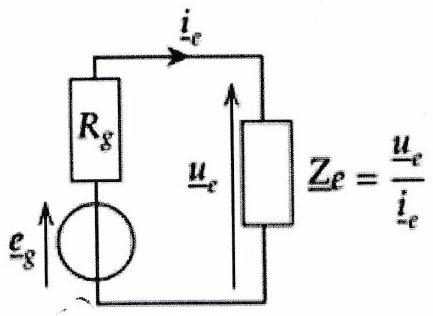
Conséquence : À quelle condition la tension en entrée du filtre s’apparente à la f.e.m délivrée par le générateur ? On suppose cette condition vérifiée pour la suite.
2 ) Impédance de sortie¶
Appelons la fonction de transfert du quadripôle en sortie ouverte (c’est-à-dire celle du quadripôle lorsque ).
Définition 2 : Impédance de sortie¶
Du point de vue de la sortie (donc depuis la charge d’impédance ), le quadripôle et la source peuvent être modélisés comme un dipôle actif linéaire, donc comme un générateur de Thévenin, de f.e.m. complexe et d’impédance interne , appelée impédance de sortie du quadripôle.
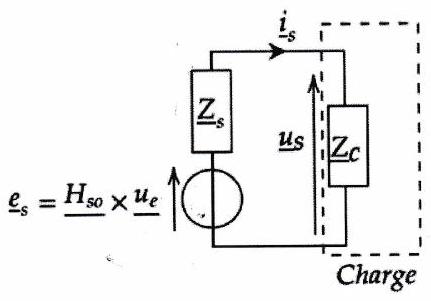
Exercice de cours à connaître 7¶
Montrer que de façon générale le comportement d’un filtre en présence d’une charge est modifié.
À quelle condition peut-on considérer que la fonction de transfert du filtre en présence d’une charge correspond à celle en sortie ouverte ?
Remarque¶
L’impédance d’un oscilloscope étant telle que , elle sera considéré grande l’impédance de sortie d’une majorité de filtre. Ainsi, les tensions de sortie des filtres pourront être observées à l’oscilloscope sans changer le comportement du filtre.
3 ) Modélisation quadripolaire¶
D’après les deux définitions précédentes, il est possible d’adopter la représentation suivante pour un filtre (modélisation quadripolaire) :
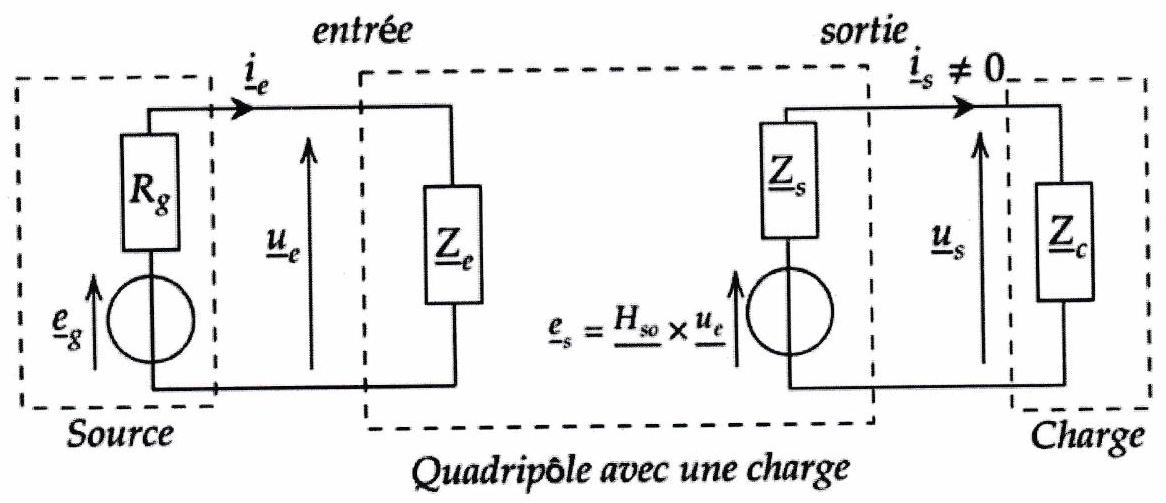
V ) Mise en cascade de filtres¶
Considérons deux filtres de fonction de transfert en sortie ouverte respective et . Lorsqu’on associe ces deux filtres en cascade (pour créer un nouveau type de filtre ou pour doubler l’effet d’un seul par exemple), la sortie du premier correspond à l’entrée du second.
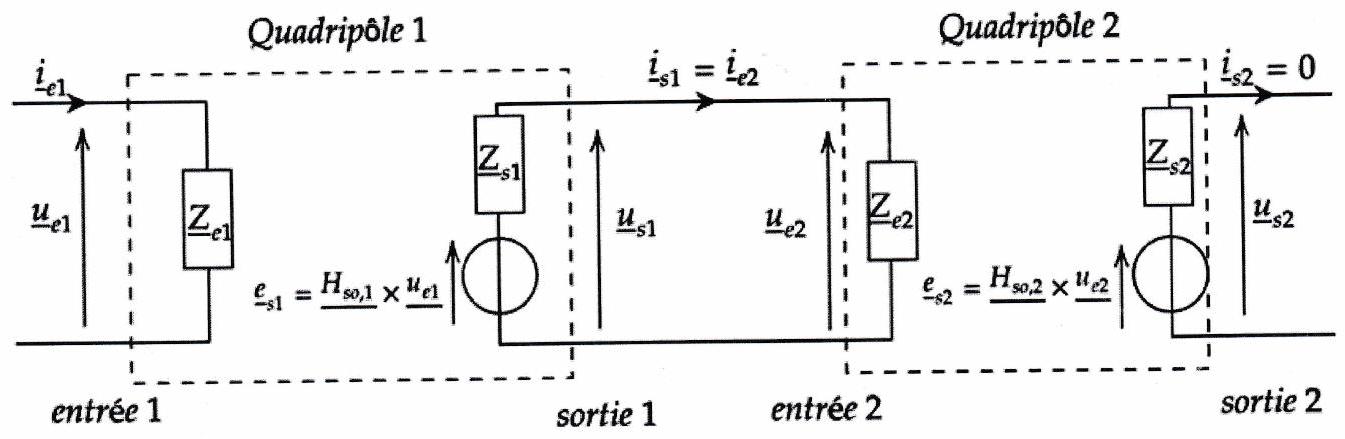
Le filtre 1 est donc chargé par la présence du filtre 2 en effet . Ainsi, si on note la fonction de transfert totale (c’est-à-dire celle du montage complet), on a dans le cas général :
Exercice de cours à connaître 8¶
Montrer que dans le cas général
Dans quelle condition il est possible
De manière générale, la fonction de transfert équivalente pour des quadripôles qui se suivent (montés en cascade) n’est pas le produit des fonctions de transfert en sortie ouverte individuelles. Afin de garantir le bon fonctionnement de ces quadripôles lorsqu’on les met en cascade, il faut réaliser des filtres de tension de faible impédance de sortie et de forte impédance d’entrée.