Methodo¶

Régression linéaire¶

1) Principe et intérêts d’une régression linéaire¶

Considerons qu’un modèle physique nous permette d’établir qu’une grandeur $y$ est reliée à une grandeur $x$ par la relation $y = ax + b$. Experimentalement, vous pourriez être amené.e.s à :

• vérifier que le modèle est juste.

• estimer la pente $a$ ou l’ordonnée à l’origine $b$, le modèle étant supposé vérifié.

Pour ce faire, on reproduit l’expérience $m$ fois : on choisit plusieurs valeurs $x_i$ avec $i \in [1:m]$ et on mesure la valeur de $y_i$ qui correspond (ou inversement). Dans les deux cas, vous serez amené.e.s à réaliser une régression linéaire. Ainsi, on obtient un ensemble d’observations $\{x_i, y_i\}$.

Principe d’une régression linéaire¶

Ainsi, une régression linéaire consiste à chercher les coefficients $a$ et $b$ tels que la quantité $ax_i + b$ soit la plus proche du point de mesure $y_i$ pour tout $i \in [1:m]$.

Remarque¶

En fait, le logiciel calcule les coefficients $a$ et $b$ de la régression linéaire de sorte à minimiser la quantité

(Méthode des moindres carrés).

Remarque¶

Le cerveau humain étant doué pour repérer les droites, cela permet en un coup d’œil de repérer si les données semblent bien se superposer sur une droite, ou plus souvent de détecter un éventuel “point aberrant”, c’est-à-dire une valeur sur laquelle vous vous êtes trompé lors de la mesure.

Seules les régressions linéaires sont capables de valider une loi en donnant l’ordre de grandeur de l’erreur à envisager. En conséquence, pour tester la validité d’une loi non-linéaire $y = f(x)$ ($f$ non linéaire), on ne trace pas $y$ en fonction de $x$ : il faut la réécrire de manière à lui donner une forme linéaire. À l’œil nu, pour juger de la validité d’un modèle linéaire. En effet :

• les points doivent être proches de la courbe... ce qui peut être délicat à juger à cause des erreurs aléatoires ;

• si l’on observe une autre tendance dans l’agencement des points expérimentaux (ex : une tendance parabolique, exponentielle...), on pourra d’ores et déjà conclure que le modèle ne peut pas être linéaire.

Cependant, la prise en compte des barres d’incertitudes facilite grandement une validation à l’œil nu.

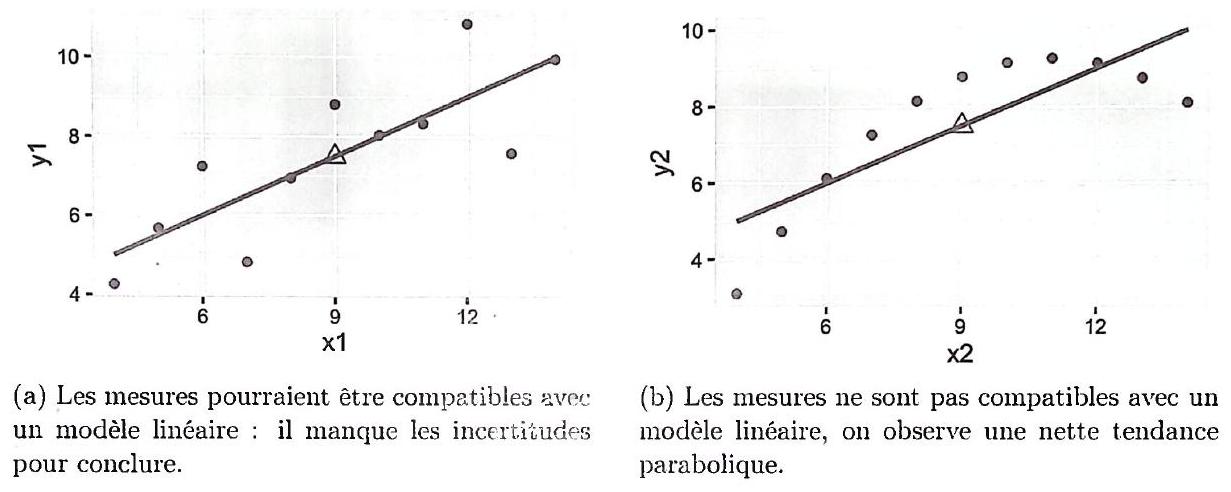
Figure 1.2: Comparaison de deux sets de données avec un modèle linéaire

$\mathbb{I I I}$ ) Tracé d’une régression linéaire avec Python¶

On décrit dans cette partie les fonctions Python permettant de réaliser une régression linéaire. Traitons l’exemple du test de la validité de la loi de Cauchy

On suppose que l’on a réalisé huit points expérimentaux, c’est-à-dire 8 couples $(n, \lambda)$.

Étape 1 : Comme d’habitude, on importe les bibliothèques nécessaires (si ce n’est pas déjà fait.)

import numpy as np
from math import *
import matplotlib.pyplot as plt

Étape 2 : On crée des tableaux dans lesquels on entre les données expérimentales.

# Données expérimentales :
indice = np.array([1.541, 1.534, 1.531, 1.531, 1.527, 1.526, 1.522, 1.520])
Lambda = np.array([404.7, 435.9, 483.0, 491.6, 512.0, 546.1, 579.0, 643.0])
Lambda = Lambda * 1e-9 # On convertit lambda en mètres

Etape 3 : On choisit $x$ et $y$ de manière à transformer la loi étudiée en loi linéaire.

x = 1 / Lambda ** 2
y = indice

Étape 4 : On effectue le calcul de la régression linéaire à l’aide de la fonction :

np.polyfit(x, y, degrépolynome)

Cette fonction prend en argument les données $x$ sur l’axe des abscisses et $y$ sur l’axe des ordonnées et le degré du polynôme pour lequel on va réaliser la régression, pour une régression linéaire, il vaut 1.

p = np.polyfit(x, y, 1) # régression linéaire de l'indice n en fonction de 1/lambda^2, n = p[0] * 1/lambda^2 + p[1]
print('pente:', p[0]) # Affiche la pente de la droite
print('ordonnée origine:', p[1]) # Affiche l'ordonnée à l'origine

Étape 5 : Enfin, on trace les données et la droite de régression sur le même graphique.

plt.plot(x, y, linestyle=' ', marker='+') # Tracé des données
plt.plot(x, np.polyval(p, x)) # Tracé de la régression
plt.show() # Pour afficher le graphique