- Méthode¶

Autour du matériel en électricité¶

Cette fiche méthode a pour but de présenter les différents instruments de mesure en électricité et leur fonctionnalité.

I) Rappels et compléments sur les signaux périodiques¶

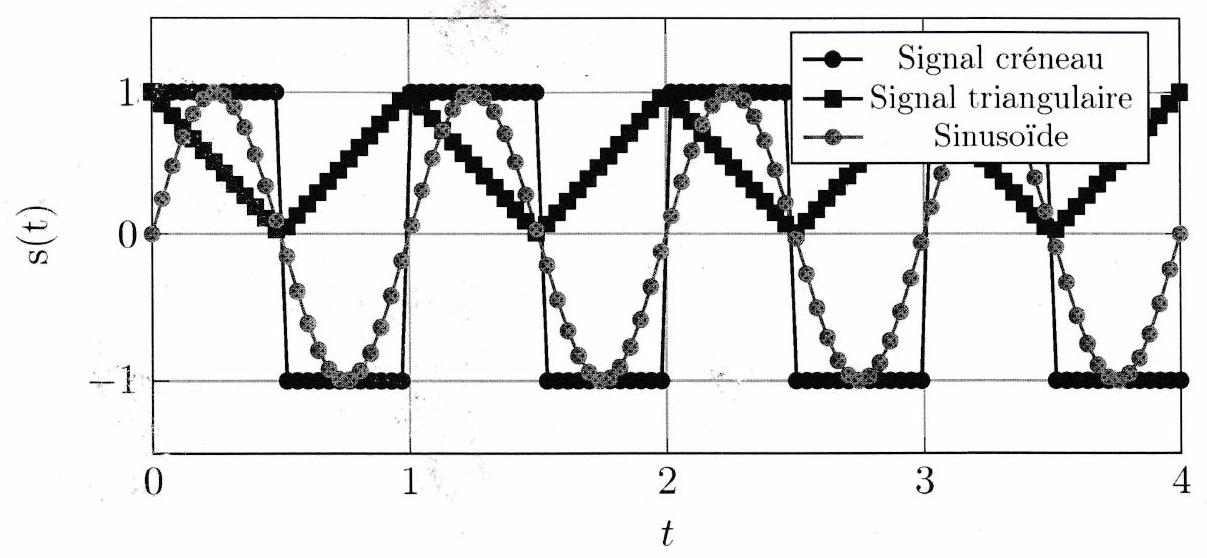
Un signal $s$ est periodique dans le temps lorsqu’il se répète identique à lui-même à intervalles de temps réguliers. La période temporelle est la plus petite durée $T$ telle que $s(t+T)=s(t)$. En TP, nous serons amenés à produire et à étudier des signaux périodiques. Les plus fréquents sont les signaux sinusoïdaux, les créneaux ou encore les signaux triangulaires.

A ) Valeur moyenne¶

On définit la valeur moyenne d’un signal périodique $s$ par : $\langle s(t)\rangle=\frac{1}{T} \int_{t=0}^{t=T} s(t) \mathrm{d} t$ :

B ) Valeur efficace

La valeur efficace d’un signal périodique est définie par

Que l’on peut écrire aussi

On parle aussi de valeur “RMS” (Root Mean Square en anglais) car c’est la racine carrée de la moyenne des carrés de la valeur instantanée sur un cycle complet.

L’origine physique de cette grandeur est purement énergétique, en régime périodique, les électroniciens ont besoin d’une grandeur physique permettant de chiffrer l’énergie d’un signal.

Origine physique¶

La valeur efficace d’une tension $u(t)$ (respectivement d’une intensité $i(t)$ ) correspond physiquement à la valeur de la tension continue $U_{e f f}$ (respectivement d’intensité continue $I_{e f f}$ ) qui produirait le même effet joule sur une période $T$ dans une résistance $R$.

En effet, sur une période $T$, une résistance $R$ reçoit l’énergie : $W_{j}=\int_{t=0}^{t=T} R i^{2}(t) \mathrm{d} t$. Par définition de la valeur efficace (valeur d’intensité continue qui produirait le même effet joule sur une période $T$ dans une résistance $R$ ) on peut aussi écrire que $W_{j}=\int_{t=0}^{t=T} R I_{\text {eff }}^{2} \mathrm{~d} t=R I_{\text {eff }}^{2} T$.

En égalant les deux expressions, on obtient :

En simplifiant par $R$, et en divisant par $T$, on obtient :

On peut suivre exactement le même raisonnement pour $U_{e f f}$.

• Travail préparatoire : Pour un signal sinusoïdal de la forme $s(t)=S_{0}+S_{m} \cos (\omega t+\varphi)$. montrer que $S_{\text {eff }}=\sqrt{S_{0}^{2}+\frac{S_{m}^{2}}{2}}$

$\_\_\_\_$ $\left\langle K s^{2}(t)\right\rangle=S_{0}^{2}+5 n^{2}$ $\_\_\_\_$

II ) Présentation du multimètre¶

A ) Mesures au multimètre¶

Un multimètre numérique peut réaliser plusieurs fonctions : Voltmètre, ampèremètre, ohmmètre.

Il possède pour cela quatre bornes d’entrée. Il permet de mesurer :

• la tension aux bornes d’un dipôle lorsqu’il est utilisé en mode voltmètre (on utilise les bornes $V$ et COM et il est branché en dérivation du dipôle considéré) ;

• une intensité en mode ampèremètre, ( on utilise les bornes ( 10 A ou $\mathrm{mA} / \mu \mathrm{A}$ et il est branché en série) ;

• une résistance (ohmmètre, branchement en dérivation).

B ) Les modes du multimètre¶

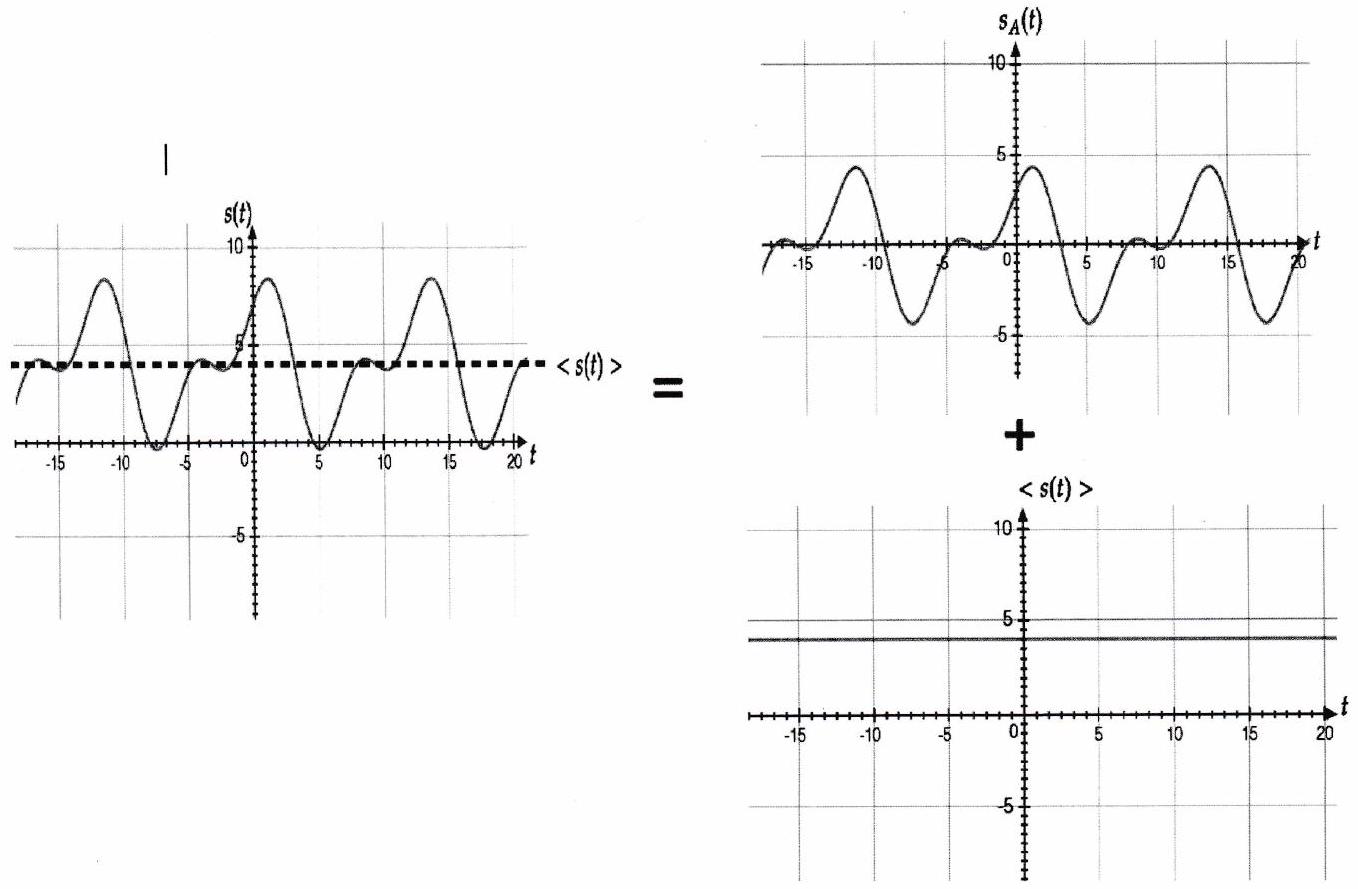
Un signal periodique $s(t)$ peut toujours s’écrire comme la somme :

• d’une composante continue : c’est la valeur moyenne $\langle s(t)\rangle$

• d’une composante alternative que l’on notera $s_{A}(t)$

En d’autres termes $s(t)$ peut s’écrire $s(t)=\langle s(t)\rangle+s_{A}(t)$ Le multimètre possède trois modes de fonctionnement accessibles par court appui sur le bouton MODE AC/DC :

• Mode DC ou “Direct Current” : C’est le mode utilisé en régime continu. En régime variable, il mesure la valeur moyenne du signal $\langle s(t)\rangle$. Donc si les grandeurs du circuit sont variables (par exemple périodiques), le mode $D C$ mesurera la valeur moyenne.

• Mode AC ou “Alternative Current” (calibre alternatif) : il mesure la valeur efficace de la composante alternative du signal, $\sqrt{\left\langle s_{A}(t)^{2}\right\rangle}=\sqrt{\left\langle(s-\langle s\rangle)^{2}\right\rangle}$ (tous les multimètres peuvent réaliser cette mesure)

• Mode AC+DC : il mesure la valeur efficace du signal complet $s_{\text {eff }}=\sqrt{\left\langle s^{2}(t)\right\rangle}$. La notation anglaise RMS signifie “root mean square” (racine de la moyenne du carré), seuls les multimètres TRMS (true root mean square) peuvent réaliser cette mesure. $\_\_\_\_$ Travail préparatoire : Pour un signal sinusoïdal de la forme $s(t)=S_{0}+S_{m} \cos (\omega t+\varphi)$. Que mesure le mode $D C$, le mode $A C$, puis le mode $A C+D C$ du multimètre.

C ) Calibre et incertitudes¶

• Touche RANGE : par appui court successif, cette touche permet de choisir manuellement un calibre de mesure. Sinon, le calibre est automatiquement choisi par le multimètre (indication écran AUTO).

• Incertitudes du multimètre : précision indiquée

Le dernier digit D correspond à la plus petite variation possible de l’affichage.

Cette incertitude correspond à la demi-étendue $\Delta$ du domaine d’appartenance de la mesure, avec une distribution uniforme. Les valeurs de $n, N$ et D donc les incertitudes dépendent du calibre utilisé “RANGE”, ces valeurs sont accessibles sur les fiches constructeur disponibles en salle de TP.

Exemple¶

Le multimètre en mode voltmètre est utilisé sur le calibre 60 V pour effectuer cette mesure, sur la fiche constructeur, on lit que pour ce calibre que la demi étendue est donnée par : $\ll 0.09 \% \mathrm{~L}+2 \mathrm{D} \gg$. Le dernier digit étant la plus petite variation possible de l’affiche, on lit $\mathrm{D}=0.1 \mathrm{~V}$. On en déduit donc que $\Delta=0.09 \% \times 34.9 V+2 \times 0.1 \mathrm{~V}$. Ainsi $\Delta=0.23 \mathrm{~V}$ donc l’incertitude $u(U)=\frac{\Delta}{\sqrt{3}}=0.1 \mathrm{~V}(1 \mathrm{CS})$ On a donc $U=(34.9 \pm 0.1) \mathrm{V}$

III ) Production d’une tension et conseils de câblage d’un circuit¶

A) Utilisation du GBF 265 ou 266¶

Le GBF est un Générateur Basses Fréquences qui délivre une tension dont on peut faire varier la forme (tension sinusoïdale, créneau ou triangulaire), la fréquence $f$ en Hz et l’amplitude $U_{m}$.

Voici le lien vers une vidéo qui explique très bien les fonctionnalités de l’appareil : https://www.youtube.com/watch?v=cNjm_dFDeXU.

Voici les fonctionnalités qui vous permettront de générer la tension de votre choix :

• Un appui sur le bouton FUNCTION permet de choisir la forme du signal. En tournant la roue codeuse vous pouvez choisir :

• Sin : tension sinusoïdale, DC : tension continue, Tri: tension triangulaire, Squ : tension créneaux (carré)

• Choix de la fréquence : On appuie sur le bouton FREQ ; le choix de la fréquence se fait en tournant la roue codeuse.

• Choix de l’amplitude du signal: Un appui sur la touche LEVEL puis le choix par la roue codeuse. Un second appui permet d’atténuer l’amplitude, qui peut se régler de 0.0 V à 2.00 V , un troisième appui permet d’atténuer une seconde fois.

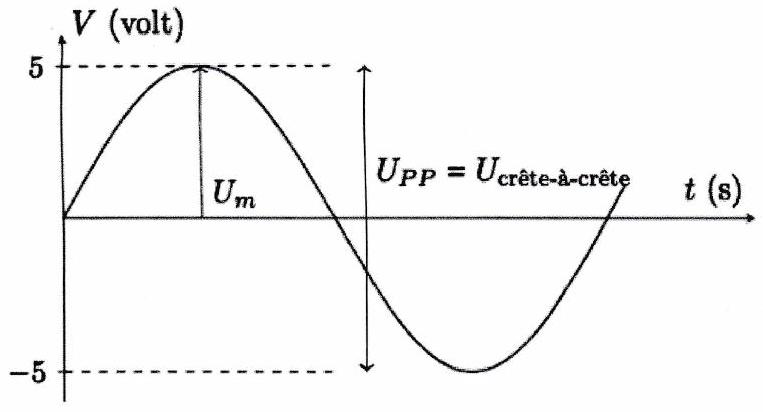
△ : Sur les GBF, il est fréquent de ne pouvoir régler que la tension crête à crête $U_{P P}$ (“peak to peak”) et non l’amplitude $U_{m}$. Sur la figure ci-contre, l’amplitude $U_{m}$ du signal vaut 5 V et la tension crête à crête vaut $U_{P P}=10 \mathrm{~V}$. Donc si on vous demande de générer une tension sinusoïdale d’amplitude $U_{m}=5 \mathrm{~V}$, il faudra régler $U_{P P}=10 \mathrm{~V}$

• Ajout d’une tension continu : un appui sur la touche OFFSET permet d’ajouter une composante continue à votre signal, le réglage de la valeur moyenne se fait à l’aide de la roue codeuse de -10 V à +10 V .

• Branchement du GBF dans un circuit : Pour relier le GBF au reste du circuit, on utilise la sortie OUTPUT $50 \Omega$ en y branchant un câble coaxial.

B ) Fiches BNC : Branchement d’un GBF ou d’un oscilloscope au circuit¶

1 ) Fiches BNC¶

Sur la façade avant des appareils (oscilloscope et GBF), la tension est relevée au niveau de la fiche BNC (voir figures 1.1 et 1.2) ; la différence de potentiel est mesurée ainsi : potentiel de la borne intérieure - potentiel de la borne extérieure

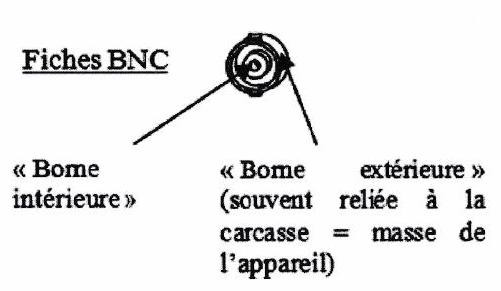
Figure 1.1: Fiche BNC

Figure 1.2: Fiche BNC d’un GBF

Les câbles qui permettent de se connecter aux fiches BNC sont des câbles coaxiaux. Utilisez de préférence des câbles coaxiaux, car ils limitent la présence de bruit dans le signal.(voir figure 1.3 )

Des adaptateurs « BNC-banane» (figure 1.4) permettent d’utiliser des fils classiques.

Figure 1.3: Câble coaxial

Figure 1.4: Adaptateur BNC-Banane

C) Masse et terre : Conseils de câblage¶

1 ) Terre¶

• EDF délivre une tension sinusoïdale de fréquence 50 Hz et de valeur efficace $U_{e f f}=S 230 \mathrm{~V}$ entre un conducteur appelé phase $(\mathrm{P})$ et un deuxième conducteur appelé neutre (N).

• EDF relie le conducteur ( N ) à la terre (point T ) par un système de faible résistance $R_{T}$, appelée résistance de terre, ce qui assure une différence de potentiel (ddp) voisine de zéro entre N et T . (voir figure 1.5)

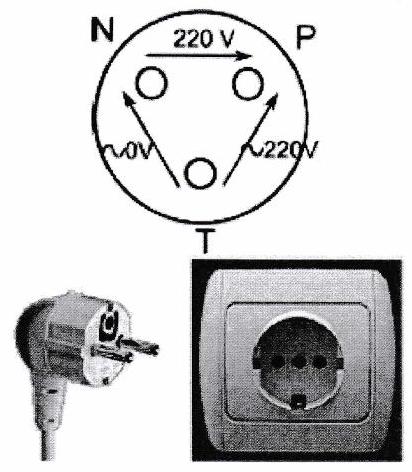
Figure 1.5: prise électrique

2 ) Masse :¶

• Dans un circuit électrique, la masse représente l’ensemble des carcasses éléments. Par exemple, dans une machine à laver, comme pour un oscilloscope ou la plupart des GBF, la carcasse métallique constitue la masse et est reliée à la borne de masse de la fiche BNC de l’appareil (Borne extérieur, voir figure 1.1).

• Un appareil (GBF ou oscilloscope) branché sur une prise secteur est presque toujours relié à la terre. Ainsi, les bornes extérieures de ses fiches BNC sont reliées entre elles et reliés à la terre.

• Le câble qui relie un appareil électrique au circuit est un câble BNC. La prise terre de l’appareil électrique est connectée à l’armature extérieure du câble (à droite sur la photo), elle-même connectée au câble noir (à gauche de la photo). Par conséquent : tous les câbles noirs des différents câbles BNC sont au même potentiel, celui de la terre !

Finalement, lorsque cet appareil est connecté à votre circuit, ce dernier est donc lui aussi relié à la terre.

Il faudra alors faire très attention lorsque l’on branche plusieurs appareils dans un même circuit (un GBF et un oscilloscope par exemple) à ne pas créer de court-circuit. Cela peut arriver plus vite que prévu! Tous les appareils électriques branchés au secteur ont donc une masse commune qui est reliée la terre.

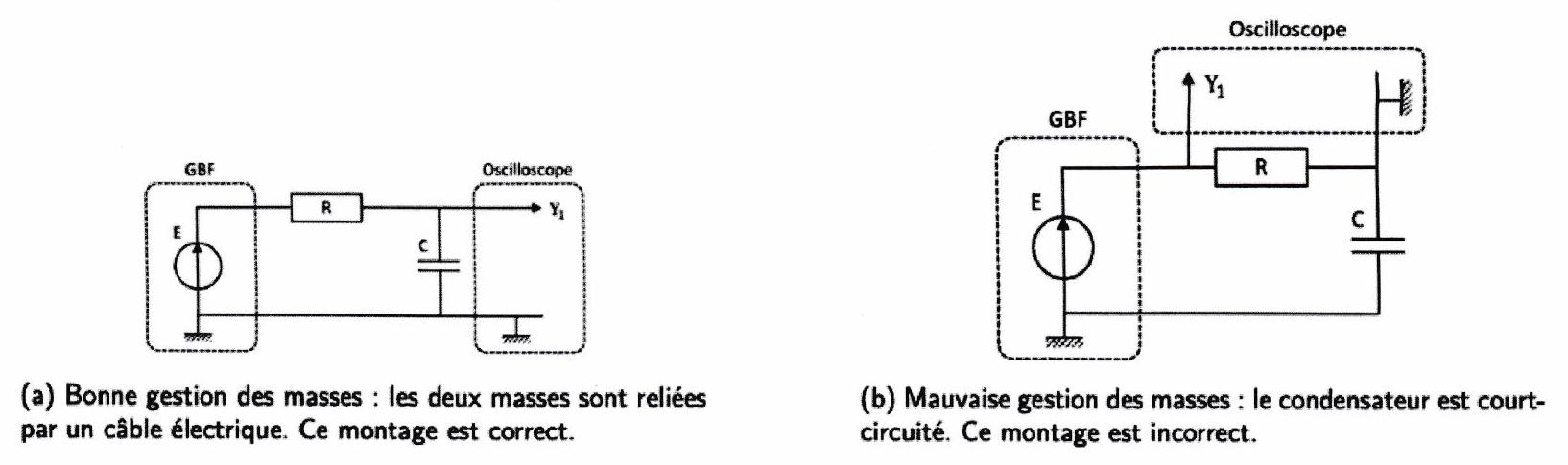
Figure 1.6: Gestion des masses

Méthode : Câbler correctement un circuit électrique AVANT de réaliser le circuit :¶

1. Représenter le schéma du circuit électrique étudié.

2. Placer les masses du GBF et de l’oscilloscope sur le schéma (elles sont reliées entre elles, car reliées à la terre).

3. Puis placer sur le schéma les appareils de mesure nécessaires (oscilloscope, voltmètre...)

Réaliser le circuit :¶

4. Réaliser le circuit étudié (SANS les appareils de mesure sauf si c’est un ampèremètre, car il est branché en série dans le circuit) avec une disposition spatiale des composants identique à celle sur le schéma.

5. Utiliser les fils noirs toujours et uniquement pour ce qui arrive à la masse (qui ne doit correspondre qu’à un seul point du circuit, donc tous les fils noirs doivent arriver au même point) et utiliser toujours et uniquement les autres couleurs pour tout le reste.

6. Placer les appareils de mesure. ENSUITE, faire quelques vérifications : (a) Vérifier que le circuit est fermé. (b) Vérifier que les fils noirs (liés aux masses des appareils) arrivent tous au même point.

D ) Règles de sécurité¶

Supposons qu’il y ait un fonctionnement anormal de l’appareil. Imaginons par exemple qu’il y ait contact entre la phase et la carcasse, la carcasse est alors porté à un potentiel de 220 V . Que se passe-t-il si quelqu’un touche la carcasse ?

1. Si la masse n’est pas reliée à la Terre :¶

L’utilisateur, de résistance $R$, est parcouru par un courant d’intensité $I=\frac{U}{R}$ et a entre sa main et ses pieds une tension U.(voir figure 1.7)

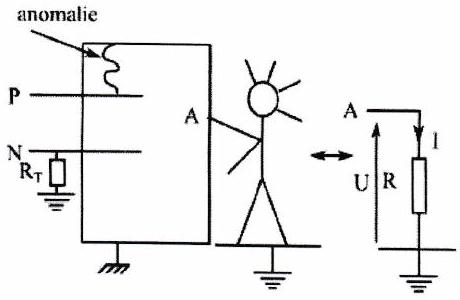
Figure 1.7: Lorsque la masse n’est pas reliée à la terre

A.N. : $U=220 \mathrm{~V}, R=2.5 \mathrm{~k} \Omega$, alors $I=88 \mathrm{~mA}$, ce qui est mortel au-delà de trois secondes... (un courant d’intensité supérieure à 30 mA peut être mortel) 2. Si la masse est reliée à la terre via $R_{T}^{\prime}$ (voir figure 1.8):

Lorsque le fil de phase entre en contact avec une carcasse métallique, le courant est instantanément évacué dans cette prise de terre : on parle alors d’un courant de fuite. Cependant, cette protection n’est que partielle, car si une personne touche la carcasse métallique, un courant de fuite va la traverser également, (faiblement si la prise de terre a été correctement réalisée).

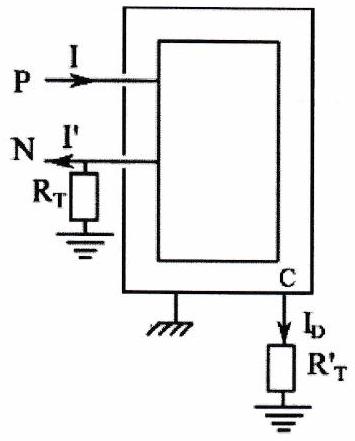
Figure 1.8: Lorsque la masse est reliée à la terre

L’installateur dispose d’un disjoncteur différentiel mesurant l’intensité $I_{D}$ du courant de fuite qui traverse $R_{T}^{\prime}$.

• En fonctionnement normal, $I=I^{\prime}, I_{D}=0 \mathrm{~A}$ et $V_{C}=V_{T}$.

• En fonctionnement anormal, la carcasse métallique est portée à une différence de potentiel $V_{C}-V_{T}=R_{T}^{\prime} I_{D}$ et $I_{D}$ devient non nulle. Le disjoncteur différentiel coupe l’alimentation électrique pour $I_{D}>I_{D, \max }$. Pour $I_{D}<I_{D, \max }$, le fonctionnement anormal doit être sans danger pour l’utilisateur. En général, les disjoncteurs différentiels sont caractérisés par $I_{D, \max }=0,3 \mathrm{~A}$.

Le disjoncteur différentiel est là pour compléter l’action de la prise de terre. En effet, si un courant de fuite existe, l’intensité du courant dans le fil neutre est différente de l’intensité du courant dans le fil de phase. Si le disjoncteur détecte une différence supérieure à une certaine valeur, il coupe immédiatement l’alimentation électrique.