Chapitre 3¶

Circuits électriques dans l’ARQS¶

Les courants électriques sont présents partout dans la vie courante : maisons individuelles, installations industrielles, appareils vidéo, ordinateurs, téléphones, aéronautique...

Dans ce chapitre, nous allons mettre en place les bases de l’électrocinétique, c’est-à-dire l’ensemble des équations permettant l’étude de tout circuit électrique, aussi bien dans le domaine industriel que dans celui de la microélectronique, tout en restant dans des domaines de fréquences usuelles de 0 HZ à plusieurs GHz.

I) Description d’un circuit électrique¶

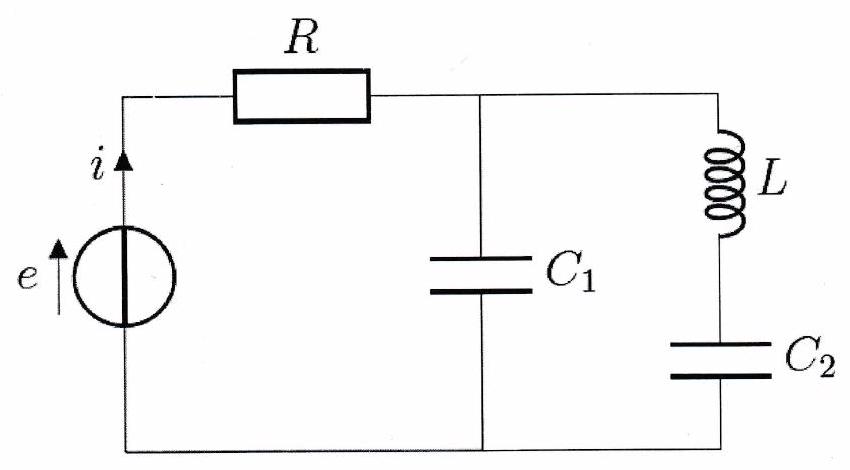
Pour illustrer les définitions qui suivent, on prend l’exemple d’un oscillateur à quartz dont un modèle simplifié est représenté ci-dessous.

Définition 1 : Circuit électrique¶

Un circuit électrique est un ensemble de conducteurs reliés entre eux par des fils de connexion et dans lequel peut circuler un courant électrique.

Définition 2 : Fil de connexion¶

Un fil de connexion est un fil conducteur dont la résistance est négligeable devant les autres résistances du circuit électrique.

Définition 3 : Dipôle¶

Un dipôle est un composant électrique connecté au circuit électrique par deux bornes.

Exemple¶

Le circuit modélisant l’oscillateur à quartz comprend cinq dipôles : un conducteur ohmique $R$, deux condensateurs $C_{1}$ et $C_{2}$, une bobine $L$ et un générateur.

Définition 4 : Nœud¶

Un nœud est un point de jonction entre plu de deux dipôles.

Exemple¶

$R, C_{1}$ et $L$ ont tous trois une borne reliée au même nœud.

Définition 5 : Branche¶

Une branche est constituée par un ensemble de dipôles montés en série entre deux nœuds.

Exemple¶

Le condensateur $C_{2}$ et la bobine $L$ sont en série et appartiennent à la même branche, $C_{1}$ est seul dans sa branche.

Définition 6 : Maille¶

Une maille est un ensemble de branches formant une boucle fermée.

Exemple¶

On peut former trois mailles dans le circuit modélisant l’oscillateur à quartz.

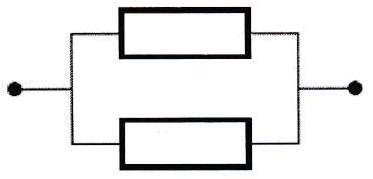
Définition 7 : Circuit en dérivation¶

Deux dipôles dont les bornes sont connectées aux mêmes nœuds sont en dérivation, ou encore en parallèle.

II ) Grandeur dans un circuit électrique¶

A) Charge et courant électrique¶

1 ) Définition¶

Définition 8 : Courant électrique¶

À l’échelle microscopique, le courant électrique est dû au mouvement des porteurs de charge électriques (électrons, ions, etc.).

Application 1¶

Identifier les porteurs de charge responsables des courants électriques dans les situations illustrées ci-dessous.

Ligne Haute Tension

2 ) Sens du courant¶

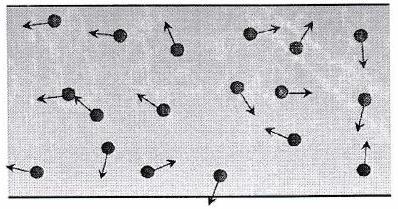
Mouvement désordonné $i=0$

Electrolyse de la saumure

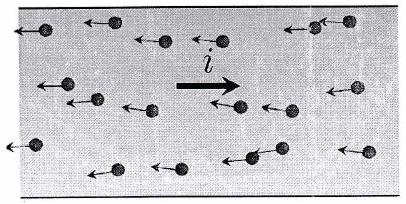
Mouvement ordonné $i \neq 0$

À l’échelle microscopique, les électrons d’un métal ont un mouvement aléatoire lié à l’agitation thermique : c’est le mouvement brownien. Dans certains cas, un mouvement collectif ordonné s’ajoute à ce mouvement désordonné : on parle de courant de charge ou de courant électrique. Par convention, le sens du courant est celui du déplacement des charges positives. C’est donc aussi le sens opposé au déplacement des porteurs de charge négative (électrons).

3 ) Intensité du courant électrique¶

L’intensité du courant notée $I$ correspond au débit de charges à travers la section du conducteur. Dans le cas où $I$ est constante, elle est définie comme :

où $\delta q$ est la charge électrique traversant la section pendant une durée $\delta t$, comptée positivement pour des charges positives allant dans le sens du courant choisi. $\delta q$ est exprimée en coulombs (C), $\delta t$ en secondes et $I$ en ampères.

Remarque¶

Dans une expérience à l’échelle macroscopique, on mesure des charges d’ordre de grandeur très supérieur à la valeur de la charge élémentaire donc la quantification de la charge ne se manifeste pas. L’intensité du courant dans un circuit électrique est donc une grandeur continue et non pas quantifiée.

Définition 9 : Intensité du courant¶

De manière générale, on définit l’intensité du courant par

Exemple¶

L’ordre de grandeur de l’intensité du courant est très variable. Citons par exemple :

• Activité neuronale $\sim 1 \mu \mathrm{~A}$;

• Électroménager $\sim 1 \mathrm{~A}$ à 10 A

• Électronique du signal (électronique des ordinateurs ou des téléphones portables) $\sim 1 \mathrm{~mA}$

• Port USB $\sim 1 \mathrm{~A}$

• Industrie $\sim 100 \mathrm{~A}$

• TGV $\sim 1 \mathrm{kA}$

• Éclair d’orage $\sim 50 \mathrm{kA}$

Le courant est un phénomène physique dont le sens dépend des conditions expérimentales, tandis que l’intensité du courant est une grandeur algébrique dont le signe dépend du sens du courant et de la convention arbitrairement choisie.

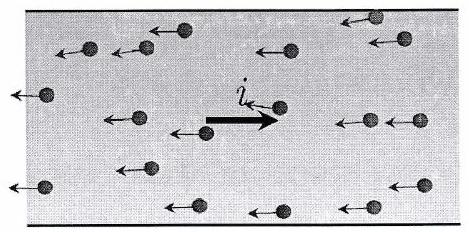
Les électrons vont vers la gauche : le sens du courant électrique est vers la droite. On choisit d’orienter $i$ vers la droite, donc $i>0$.

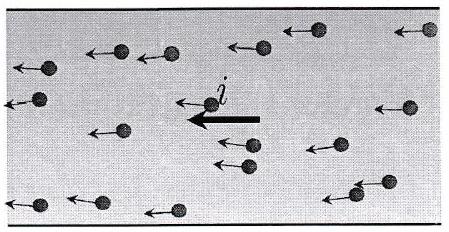
Les électrons vont vers la gauche : le sens du courant électrique est vers la droite. On choisit d’orienter $i$ vers la gauche, donc $i<0$.

4 ) Conservation de la charge¶

La charge électrique ne peut être ni créée, ni détruite : la conservation de la charge électrique est une loi fondamentale de la physique.

Un générateur ne crée aucune charge électrique, mais communique à ces dernières de l’énergie, il met les charges en mouvement.

5 ) Mesure d’intensité¶

On mesure l’intensité d’un courant à l’aide d’un ampèremètre placé en série dans la branche étudiée. Un ampèremètre idéal est équivalent à un fil de résistance nulle. En pratique, les ampèremètres réels possèdent une résistance interne très faible, de l’ordre de quelques dixièmes d’ohm.

B ) Potentiel électrique et tension¶

1 ) Définition¶

Un générateur (par exemple une pile) met les porteurs de charge en mouvement. Il leur communique de l’énergie qu’ils véhiculent dans le reste du circuit. Pour quantifier cette énergie, on définit la notion de potentiel électrique, noté $V$ et exprimé en volts.

Définition 10 : Tension électrique¶

La tension électrique $U_{A B}$ entre deux points $A$ et $B$ de potentiels électriques respectifs $V_{A}$ et $V_{B}$ est définie comme la différence de potentiel électrique entre ces deux points :

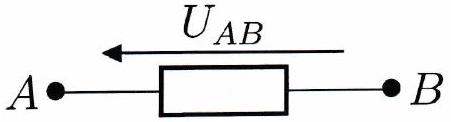
Exemple¶

L’ordre de grandeur de la tension électrique est très variable. Citons par exemple :

• Activité neuronale $\sim 0,1 \mathrm{~V}$;

• Électronique du signal (électronique des ordinateurs ou des téléphones portables) $\sim 0,1 \mathrm{~V}$

• Port USB 5 V

• Électroménager 230 V

• Industrie 400 V

• TGV 10 kV

• Éclair d’orage $\sim 1 \mathrm{GV}$

Deux nœuds reliés par un fil idéal, c’est-à-dire un fil de résistance nulle, ont le même potentiel électrique.

2 ) Additivité des tensions¶

Additivité des tensions¶

Pour deux dipôles reliés à un même nœud, comme dans la branche ci-dessous, on a

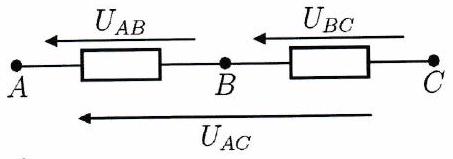
On appelle cette relation la loi d’additivité des tensions.

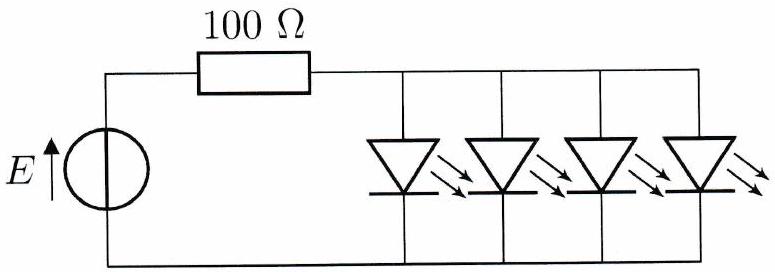
Expérience 1 : LED en série ou en dérivation¶

• Alimentation continue $E=5 \mathrm{v}$;

• LED rouges et vertes $\times 4$.

• $R=100 \Omega$;

Réaliser et comparer les deux circuits représentés ci-dessous en ajoutant une LED après l’autre. Comment expliquer les différences constatées, sachant que les LED ont une tension de seuil $V_{\text {seuil }}=1,6 \mathrm{~V}$ à $2,0 \mathrm{~V}$.

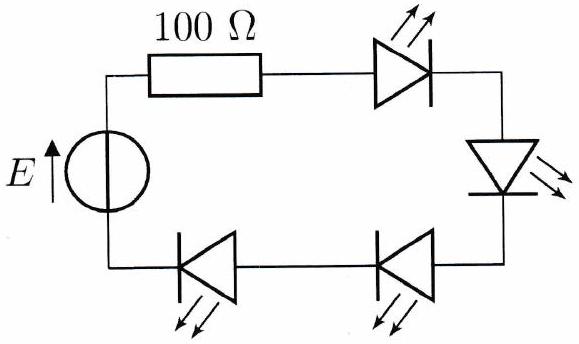
3 ) Notion de masse¶

On peut ajouter aux potentiels électriques de tous les nœuds d’un circuit un potentiel arbitraire $V_{0}$ sans changer les tensions aux bornes des dipôles. Le potentiel est toujours défini par rapport à une référence. En pratique, on choisit arbitrairement d’annuler le potentiel en un point du circuit, Cette référence de potentiel correspond à la masse du circuit, représentée par le symbole ர7.

Définition 11 : Masse¶

La masse est le point de potentiel nul : $V_{M}=0$

Lorsque le symbole de masse est représenté en plusieurs points d’un circuit cela signifie que tous ces points sont reliés entre eux et qu’ils sont tous au potentiel nul.

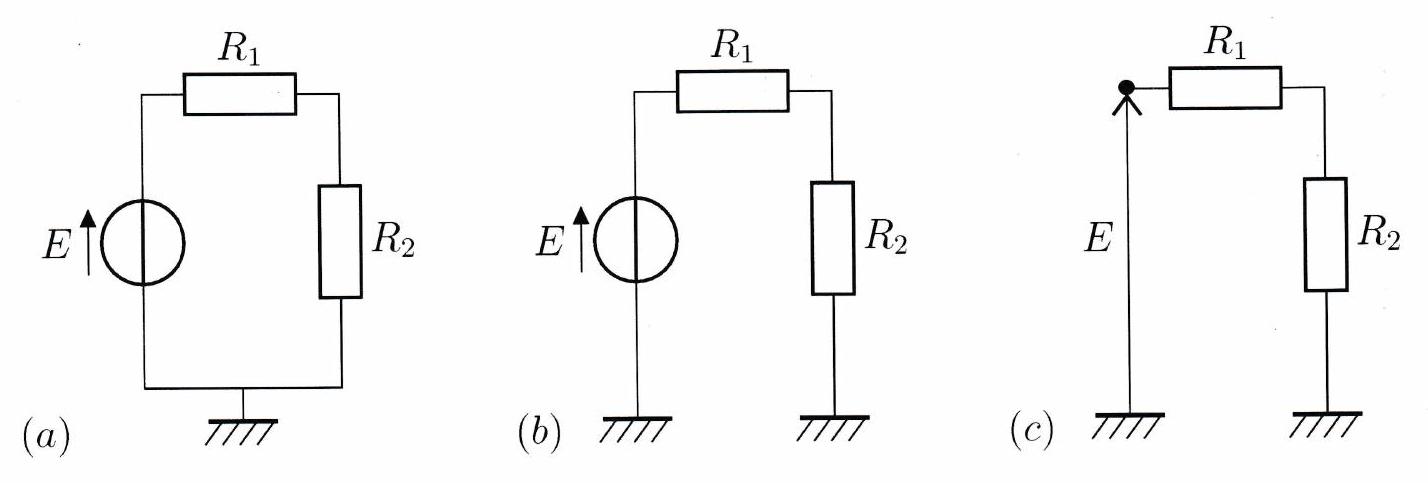
Figure 3.1: (a): un circuit électrique;(b): représentation où la connexion par la masse est implicite ; (c) : représentation où le générateur de tension est représenté par le potentiel qu’il impose au nœud.

4 ) Mesure de tension¶

On mesure une tension à l’aide d’un voltmètre placé en dérivation aux bornes du dipôle étudié. Un voltmètre idéal est équivalent à un interrupteur ouvert de résistance infinie. En pratique, les voltmètres réels ont une résistance d’entrée très élevée, de l’ordre de plusieurs megaohms,

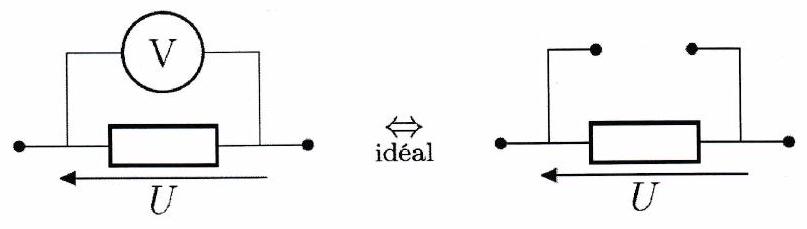
voire plusieurs centaines de megaohms.

III ) Lois de Kirchhoff¶

A) Approximation des régimes quasi stationnaires (ARQS)¶

L’électrocinétique est le domaine de l’électromagnétisme où les manifestations du mouvement des porteurs de charges sont étudiées en termes de courants et de tensions.

1 ) Régime indépendant du temps¶

Si ces grandeurs sont constantes dans le temps, nous parlerons de régime indépendant du temps ou encore de régime stationnaire. Ces grandeurs sont alors généralement notées avec des lettres majuscules : $I$ pour l’intensité et $U$ pour la tension.

2 ) Régime variable¶

Si les tensions $u(t)$ et les intensités $i(t)$ dépendent du temps, on est en régime variable. Les intensités et les tensions sont des grandeurs qui se propagent dans les conducteurs avec une vitesse finie (de l’ordre de $c=3,00 \cdot 10^{8} \mathrm{~m} \cdot \mathrm{~s}^{-1}$, vitesse de la lumière dans le vide). Ainsi, rigoureusement, il n’est plus possible de parler d’intensité $i(t)$ à un instant donné $t$ dans un circuit, car sa valeur dépend du point où nous l’évaluons.

Le temps de propagation de l’intensité dans un circuit de longueur $l$ est $\tau=\frac{l}{c}$ où $c$ est sa vitesse de propagation. Si les temps intervenant dans l’étude du circuit (période, temps de montée du signal, temps d’acquisition des mesures, ...) sont grands devant $\tau$, les phénomènes de propagation ne se manifestent pas et il sera pertinent de les négliger. Un régime variable permettant cette approximation est un régime quasi permanent ou quasi stationnaire.

Approximation des régimes quasi stationnaires (ARQS)¶

Dans l’approximation des régimes quasi stationnaires (ARQS), tous les effets liés à la propagation des signaux sous forme de tensions ou de courants sont négligés. l’ARQS est applicable pour l’étude d’un courant électrique si la longueur $l$ des fils et le temps caractéristique de variation $T$ de l’intensité sont tels que $\left(c=3,00 \cdot 10^{8} \mathrm{~m} \cdot \mathrm{~s}^{-1}\right.$ est la vitesse de la lumière dans le vide) :

Toutes les expériences de travaux pratiques d’électricité sont réalisées dans le cadre de l’ARQS. Pour la suite de ce chapitre, nous nous placerons dans le cadre de l’ARQS.

3 ) Conservation de la charge dans l’ARQS¶

Dans le cadre de l’ARQS, un fil conducteur reste électriquement neutre. Pour conserver cette neutralité, il est nécessaire que la charge entrant par la section $S_{1}$ soit égale à la charge sortant par la section $S_{2}$. En termes d’intensité, cela se traduit par :

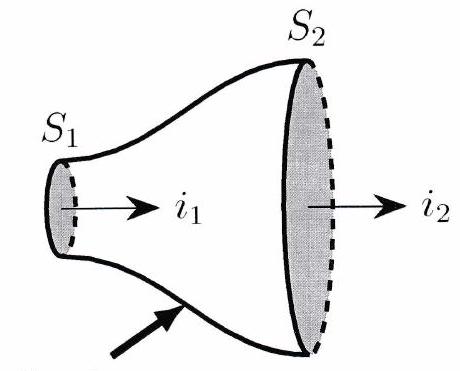
Conducteur

Dans le cadre de l’ARQS, l’intensité est la même en tout point d’un circuit sans dérivation.

Dans une branche, l’intensité est la même en tout point. Ainsi l’intensité du courant électrique qui traverse deux dipôles en série est la même.

B ) Première loi de KirchHoff : Loi des nœuds¶

De la conservation de la charge dans l’ARQS découle aussi une loi reliant les intensités au niveau d’un nœud.

Première loi de Kirchhoff : lois des nœuds¶

Au niveau d’un nœud, la somme des intensités des courants entrants est égale à la somme des intensités des courants sortants :

où $\varepsilon_{k}=+1$ si le courant $i_{k}$ aboutit sur le nœud et -1 s’il en repart. Cette loi est valable en régime stationnaire ou dans le cadre de l’ARQS.

Exemple¶

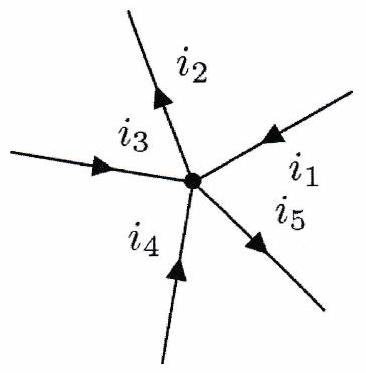
Exercice de cours à connaître 1¶

Démontrer la première loi de KIRCHHOFF en utilisant la conservation de la charge dans l’ARQS.

Application 2¶

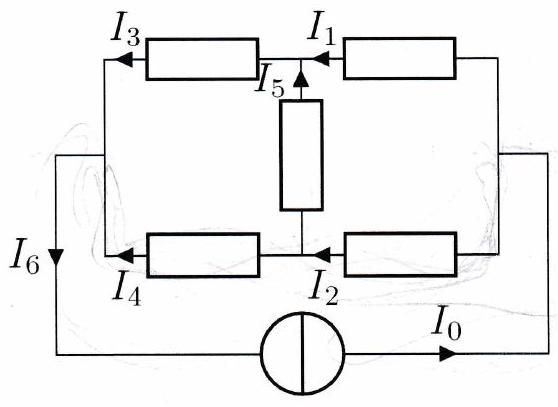
À l’aide d’un ampèremètre, on mesure l’intensité du courant en quelques points du circuit représenté cicontre. On relève $I_{0}=4 \mathrm{~A}, I_{1}=1 \mathrm{~A}$ et $I_{4}=2 \mathrm{~A}$.

1. Déterminer les intensités $I_{2}, I_{3}$ et $I_{5}$.

2. Calculer le nombre d’électrons qui traversent le générateur chaque seconde.

Données : $e=1,6 \cdot 10^{-19} \mathrm{C}$

C ) Deuxième loi de Kirchhoff : Loi des mailles¶

Cette deuxième loi est quant à elle une conséquence de l’additivité des tensions. Après avoir défini arbitrairement l’orientation d’une maille, on peut utiliser la loi des mailles. Cette loi se démontre facilement en faisant intervenir les potentiels des nœuds de la maille.

Deuxième loi de Kirchhoff : loi des mailles¶

Dans une maille, la somme algébrique des tensions est nulle :

où $\varepsilon_{k}=+1$ si la tension $u_{k}$ est orientée dans le même sens que la maille, $\varepsilon_{k}=-1$ sinon.

Exemple¶

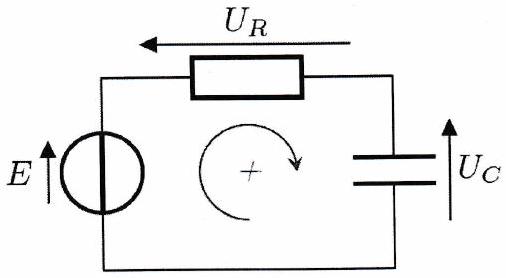
Application 3¶

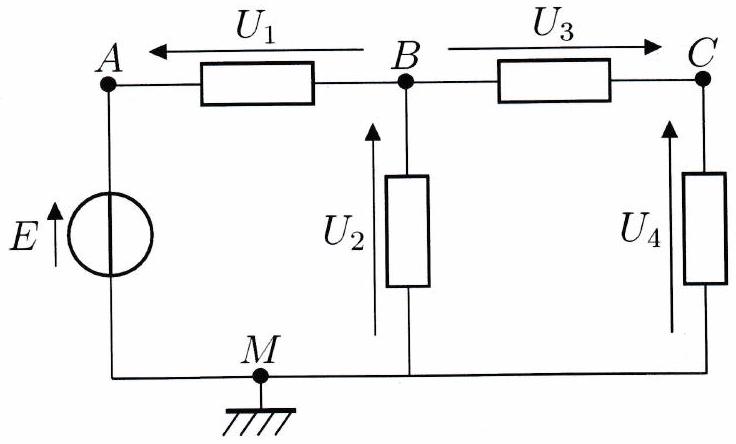
À l’aide d’un voltmètre, on mesure les tensions : $E=5 \mathrm{~V}, U_{1}=3 \mathrm{~V}$ et $U_{4}=1 \mathrm{~V}$.

1. Déterminer les tensions $U_{2}$ et $U_{3}$.

2. Déterminer les potentiels aux nœuds $A$ et $C$.

IV ) Dipôles électriques¶

La tension aux bornes de chacun des dipôles courants (résistor, condensateur et bobine) et l’intensité du courant qui les traverse vérifient une relation appelée loi de comportement. Cette loi doit impérativement être accompagnée d’un schéma et/ou d’une indication pour préciser la convention choisie !

A) Convention générateur et récepteur¶

Avant de pouvoir étudier un dipôle, il faut préciser la convention choisie pour ce dernier.

Définition 12 : Convention générateur et récepteur¶

• La convention générateur consiste à prendre le sens positif conventionnel du courant et la flèche définissant la tension dans le même sens.

• La convention récepteur consiste à prendre le sens positif conventionnel du courant et la flèche définissant la tension dans des sens opposés

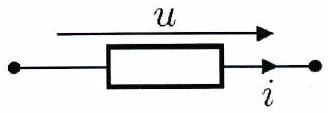
convention générateur

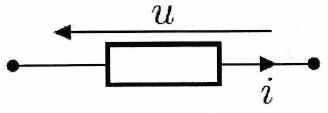
convention récepteur

Remarque¶

La convention choisie ne préjuge en rien de la nature du dipôle étudié.

B ) Puissance et énergie dans un circuit électrique¶

Rappel¶

L’énergie est une grandeur qui se conserve toujours : elle ne peut être créée ni disparaître. Pour faire varier l’énergie $\mathcal{E}$ (en Joules) d’un système, on peut lui en fournir ou il peut en céder. La puissance $\mathcal{P}$ (en Watt) correspond à la quantité d’énergie échangée par unité de temps :

L’état d’un dipôle électrocinétique est déterminé par trois grandeurs :

• l’intensité $i$ du courant qui le traverse;

• la tension $u$ à ses bornes;

• la puissance $\mathcal{P}$ qu’il échange avec le reste du circuit électrique.

Définition 13 : Puissance électrique¶

La puissance électrique $\mathcal{P}$ permet de quantifier les échanges énergétiques entre un dipôle et le reste du circuit. Elle est définie par :

où $u$ est la tension aux bornes du dipôle et $i$ l’intensité du courant qui le traverse. Son interprétation dépend de la convention choisie :

• en convention générateur, $\mathcal{P}$ est la puissance fournie par le dipôle au reste du circuit ;

• en convention récepteur, $\mathcal{P}$ est la puissance reçue par le dipôle de la part du reste du circuit.

Exemple¶

Quelques ordres de grandeur de puissance :

• puissance électrique totale produite en France : 135 GW ;

• puissance électrique fournie par un réacteur nucléaire : 1 GW ;

• puissance électrique consommée par un foyer français moyen : 500 W ;

• puissance électrique consommée par un ordinateur : 100 W ;

• puissance électrique consommée par une lampe LED : 10 W .

Application 4¶

1. En fonctionnement normal, indiquer le signe de la puissance électrique : reçue par une lampe ; fournie par un radiateur ; reçue par une centrale nucléaire ; fournie par une batterie de smartphone.

2. Indiquer si les dipôles suivants se comportent comme des générateurs ( $\mathcal{P}_{\text {fournie }}>0$ ) ou comme des récepteurs $\left(\mathcal{P}_{\text {reçue }}>0\right)$ :

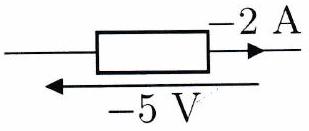
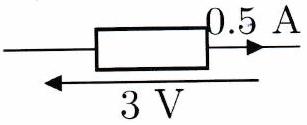
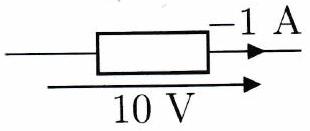
3. Calculer l’énergie électrique consommée par un radiateur de 1 kW pendant une heure.

C ) Caractéristique d’un dipôle en courant continu¶

1 ) Définitions¶

Définition 14 : Caractéristique¶

En courant continu, un dipôle se définit par la loi qui relie l’intensité $I$ du courant le traversant et la tension $U$ à ses bornes. Cette loi se traduit par un graphique expérimental donnant $I$ en fonction de $U$ appelé caractéristique du dipôle.

Lorsque la caractéristique est une droite on dit que le dipôle est linéaire. Dans le cas contraire, le dipôle est dit non linéaire.

Définition 15 : Dipôles actifs et passifs¶

On classe les dipôles en deux catégories :

• Un dipôle actif est un dipôle dont la caractéristique ne passe pas par l’origine du graphique. La tension à ses bornes n’est pas nulle même s’il n’est parcouru par aucun courant.

• Un dipôle passif est un dipôle dont la caractéristique passe par l’origine du graphique. Il n’est traversé par aucun courant si aucun générateur n’impose à ses bornes une tension non nulle.

a) Caractéristique d’un dipôle actif.
b) Caractéristique d’un dipôle passif.¶

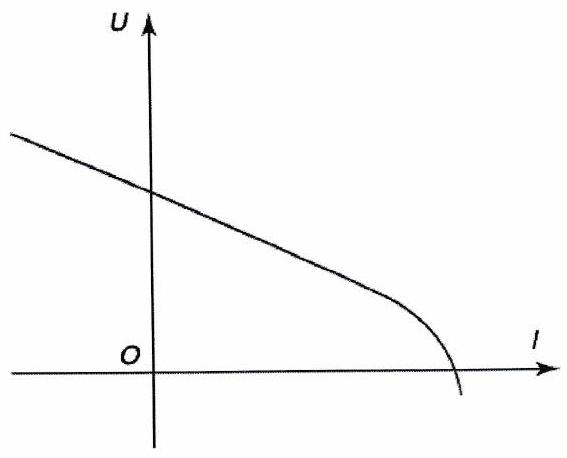
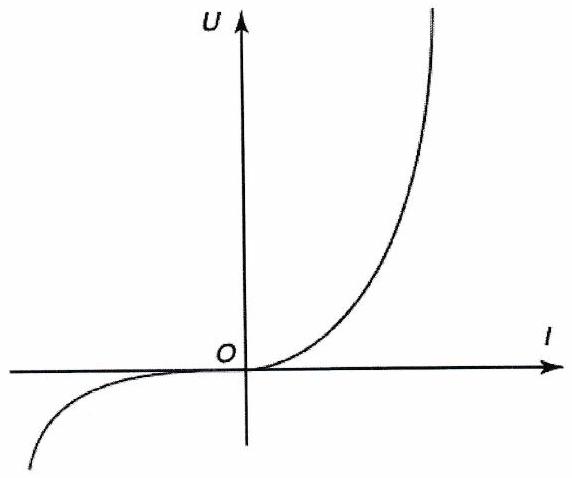
2 ) Point de fonctionnement¶

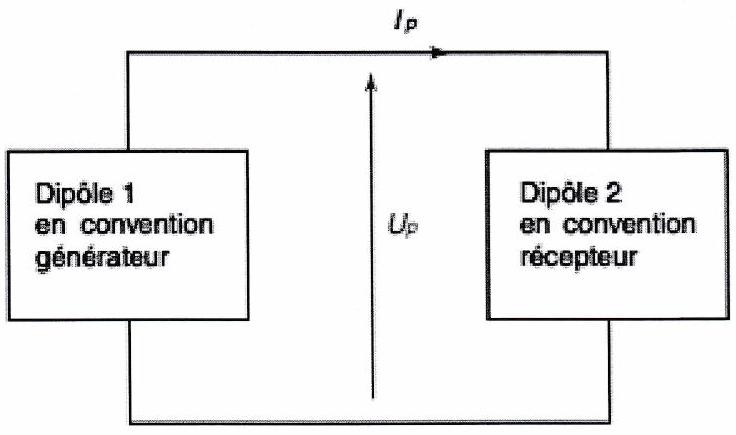
On considère un circuit formé par deux dipôles, un dipôle actif jouant le rôle de générateur et un dipôle passif jouant le rôle de récepteur. On connaît les caractéristiques des deux dipôles.

Définition 16 : Point de fonctionnement¶

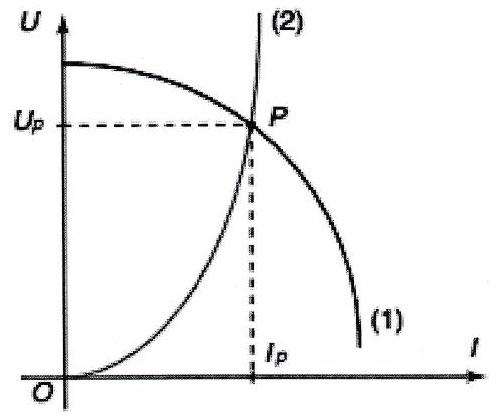
L’intersection des caractéristiques des deux dipôles est appelée point de fonctionnement. Les coordonnées ( $U, I$ ) de cette intersection donne la valeur de la tension $U$ et de l’intensité $I$ du courant aux bornes des deux dipôles.

Point de fonctionnement d’un circuit¶

En noir, caractéristique du dipôls (1) En couleur, caracteristique du dipöls (2)

D ) Conducteur ohmique¶

1 ) Loi de comportement et puissance¶

Définition 17 : Conducteur ohmique¶

On appelle conducteur ohmique tout dipôle qui vérifie la loi d’OHM. Avec $R$ la résistance du dipôle exprimées en ohms $(\Omega)$ et en convention récepteur, on a :

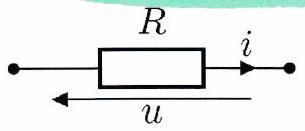
Les résistors sont réalisés avec des mauvais conducteurs électriques (céramiques ou des fils d’alliages métalliques de section modeste) : elles résistent au passage du courant électrique.

Remarque¶

En TP, on utilisera des résistors dont la résistance varie entre quelques dizaines d’ohms et quelques $\mathrm{M} \Omega$.

Application 5¶

On souhaite allumer une LED rouge ( $U_{\text {seuil }}=2,0 \mathrm{~V}, I_{\text {max }}=20 \mathrm{~mA}$ ) avec la sortie 13 d’une carte Arduino, capable de fournir une tension $E=5,0 \mathrm{~V}$. Pour protéger la carte et limiter le courant traversant la LED, on la branche en série avec un résistor de valeur $R$.

1. Déterminer la valeur $R$ à choisir.

2. Calculer la puissance électrique reçue par la LED. Comment est-elle dissipée ?

3. Exprimer et calculer la puissance électrique reçue par le résistor en fonction de $R$ et de la tension $U$ aux bornes de la résistance, puis en fonction de $R$ et de l’intensité du courant $I$ traversant la résistance. Comment est-elle dissipée ?

Puissance reçue par un résistor¶

Toute la puissance électrique $\mathcal{P}_{J}$ reçue par un résistor est dissipée par effet Joule sous forme d’énergie thermique. On a :

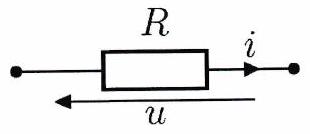
2 ) Association de résistors¶

Afin de simplifier les circuits électriques (et donc les calculs), il est parfois intéressant d’associer des résistors entre eux afin de n’en former qu’un seul. Pour cela, deux règles sont applicables.

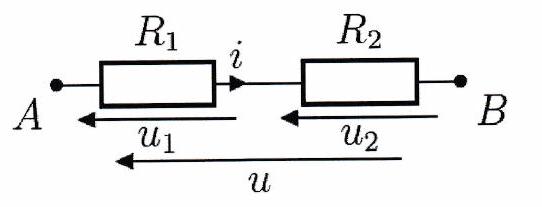
Association de résistors en série¶

Deux résistors de résistance respective $R_{1}$ et $R_{2}$ en série sont équivalentes à un unique résistor de résistance $R_{\text {éq }}$, avec

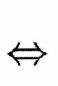
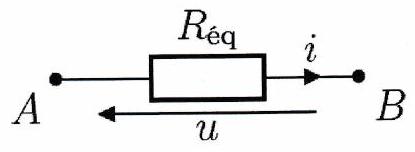
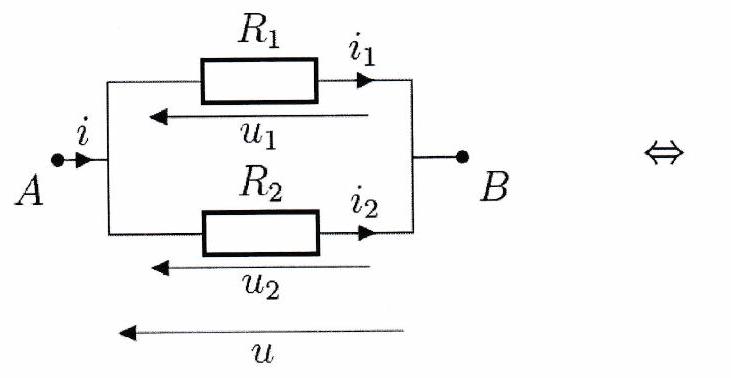
Association de résistors en dérivation¶

Deux résistors de résistance respective $R_{1}$ et $R_{2}$ en dérivation sont équivalentes à un unique résistor de résistance $R_{\text {éq }}$, avec

Exercice de cours à connaître 2¶

1. En utilisant la loi d’additivité des tensions et la loi d’OHM, démontrer la règle d’association des résistors en série.

2. En utilisant la loi des nœuds et la loi d’OHM, démontrer la règle d’association des résistors en dérivation.

Application 6¶

On ne dispose que de trois résistors de résistance respective : $R_{1}=100 \Omega, R_{2}=200 \Omega$ et $R_{3}=300 \Omega$. Comment obtenir, à l’aide d’une association de ces résistances, la valeur nécessaire au circuit de l’application 5 ?

Remarque¶

Pour $n$ résistors en série (resp. en parallèle), on a

3 ) Pont diviseur¶

Exercice de cours à connaître 3¶

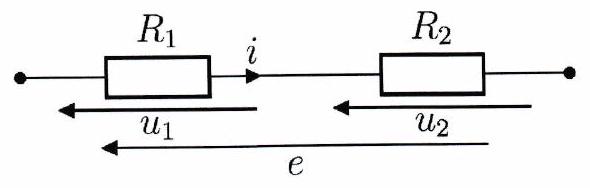
On considère un circuit composées de deux résistors de résistance respective $R_{1}$ et $R_{2}$ en série, alimentées par un générateur idéal de tension. On note $E, U_{1}$ et $U_{2}$ les tensions aux bornes du générateur, du résistor de résistance $R_{1}$ et du résistor de résistance $R_{2}$ respectivement, et $I$ l’intensité du courant qui traverse le générateur.

1. Faire un schéma en indiquant toutes les grandeurs électriques et en adoptant les conventions les plus raisonnables pour chaque dipôle.

2. Exprimer l’intensité $I$ en fonction de $E, R_{1}$ et $R_{2}$.

3. En déduire les tensions $U_{1}$ et $U_{2}$ aux bornes de chaque résistor en fonction des mêmes paramètres.

On modifie le montage précédent : les deux résistors sont maintenant montés en dérivation aux bornes du générateur. 4. Exprimer les intensités $I_{1}$ et $I_{2}$ des courants qui traversent les deux résistors en fonction de $I, R_{1}$ et $R_{2}$.

Cette application peut être résolue plus rapidement encore en reconnaissant dans les circuits étudiés des ponts diviseurs.

Pont diviseur de tension¶

Un pont diviseur de tension est formé par l’association de deux résistors en série. On a alors

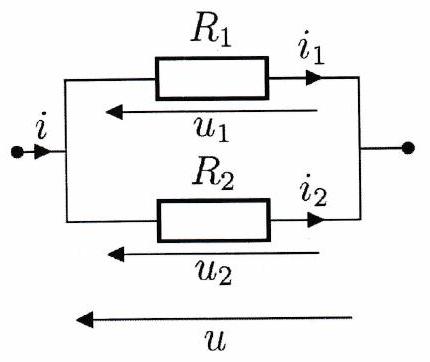
Pont diviseur d’intensité¶

Un pont diviseur d’intensité est formé par l’association de deux résistors en dérivation. On a alors

Application 7¶

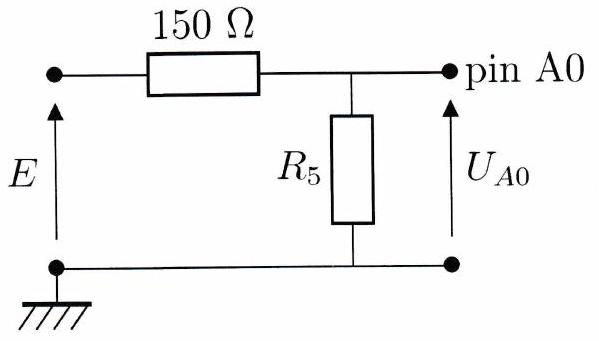
Les cartes Arduino possèdent quelques entrées analogiques ayant une résistance d’entrée très élevée, de l’ordre de $100 \mathrm{M} \Omega$. Avec l’une de ces cartes, on souhaite mesurer la tension $E$ aux bornes d’un générateur dont la tension de sortie peut monter jusqu’à 15 V . Comme les autres, l’entrée analogique $A_{0}$ de l’Arduino ne peut mesurer des tensions que si elles sont comprises entre 0 et 5 V . Par ailleurs, les résistors couramment utilisés en électronique sont dites « quart de watt » car la puissance qu’ils reçoivent ne doit pas dépasser $0,25 \mathrm{~W}$, sous peine de les endommager de manière irréversible.

1. Exprimer, puis calculer la valeur de la résistance $R_{5}$ à utiliser pour pouvoir mesurer toutes les valeurs de $E$ tout en exploitant toute la plage de mesure de l’Arduino.

2. Exprimer et calculer la puissance maximale reçue par le résistor de résistance $R_{5}$. Commenter.

3. On remplace $R_{5}$ par une association de deux résistors de résistance $2 R_{5}$ en parallèle. Exprimer et calculer la puissance maximale reçue par chacune de ces résistors. Commenter.

E ) Condensateur idéal¶

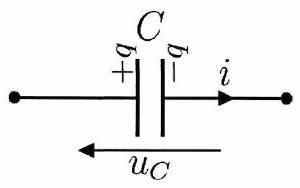
Un condensateur est un dipôle formé de deux armatures métalliques séparées par un isolant électrique. En présence d’un courant électrique, les armatures du condensateur accumulent une charge $q(+q$ pour l’une et $-q$ pour l’autre), ces charges donnent naissance à une différence de potentiel.

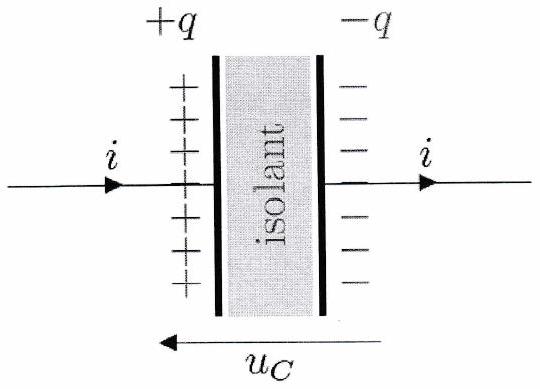
Définition 18 : Charge d’un condensateur¶

La charge électrique $q$ du condensateur est liée à sa capacité électrique $C$, exprimée en farad (F), par la relation :

Remarque¶

Le farad est une unité forte : 1 F correspond à une très grande capacité. En TP, on utilisera des condensateurs dont la capacité va de 1 pF à quelques mF .

Loi de comportement d’un condensateur¶

En convention récepteur, l’intensité du courant qui “traverse” le condensateur est liée à la tension à ses bornes

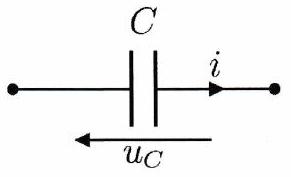
En régime stationnaire, le condensateur se comporte comme un interrupteur ouvert. Il permet notamment de stocker de l’énergie électrique pour délivrer rapidement des forts courants.

Énergie stockée dans un condensateur¶

L’énergie emmagasinée par un condensateur chargé sous une tension $u_{C}$ est

Dans un condensateur, l’énergie est stockée sous forme électrique.

Exercice de cours à connaître 4¶

Démontrer l’expression de l’énergie stockée dans un condensateur en exprimant la puissance reçue par un condensateur puis en utilisant la loi de comportement pour faire apparaître une dérivée connue.

F ) Bobine idéale¶

Une bobine est un dipôle constitué d’un bobinage de fil enroulé autour d’un axe (souvent autour d’un matériau ferromagnétique). Son principe de fonctionnement sera détaillé dans des chapitres ultérieurs.

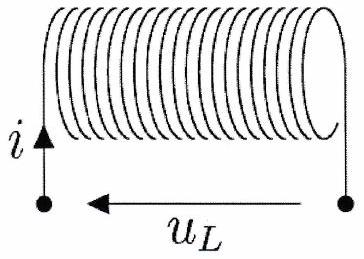
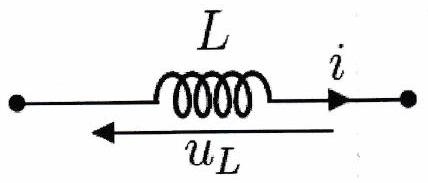
Loi de comportement d’une bobine¶

Une bobine est caractérisée par son inductance $L$ (ou auto-inductance) exprimée en henry $(H)$. En convention récepteur, l’intensité du courant qui traverse une bobine d’inductance $L$ est liée à la tension à ses bornes :

Remarque¶

L’inductance des bobines utilisées en TP varie entre quelques $\mu \mathrm{H}$ et 1 H . En régime stationnaire, la bobine se comporte comme un fil. Elle peut stocker de l’énergie pour créer brièvement de fortes tensions.

Énergie stockée dans une bobine¶

L’énergie emmagasinée par une bobine parcourue par un courant d’intensité $i$ est

Dans une bobine, l’énergie est stockée sous forme magnétique.

Exercice de cours à connaître 5¶

Démontrer l’expression de l’énergie stockée dans une bobine en exprimant la puissance reçue par une bobine puis en utilisant la loi de comportement pour faire apparaître une dérivée connue.

G ) Générateurs¶

Il existe deux types de générateurs :

• des sources de courant, qui délivrent un courant choisi par l’utilisateur :

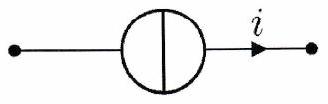
• des sources de tension, qui imposent une tension choisie par l’utilisateur :

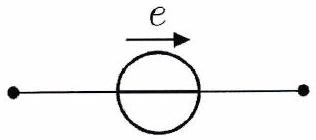
Définition 19 : Source idéale de tension¶

Une source idéale de tension impose une tension constante quel que soit le circuit qu’elle alimente, et donc quelle que soit l’intensité du courant qu’elle fournit.

Ce modèle simple ne permet cependant pas d’expliquer le fonctionnement des sources réelles.

Expérience 2 : Chute de tension aux bornes d’un GBF¶

• GBF ;

• oscilloscope ;

• fils ;

• boîte à décade de résistance.

Que peut-on dire de la tension aux bornes du générateur lorsqu’on diminue la résistance de charge ?

Définition 20 : Modèle de Thévenin¶

On peut modéliser une source de tension réelle avec le modèle de Thévenin, comme l’association d’une source idéale de tension de force électromotrice (f.é.m.) e en série avec un résistor de résistance $r$.

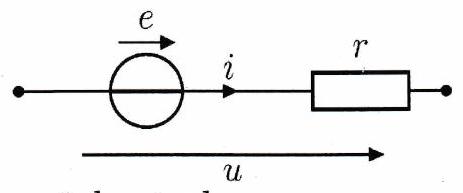
En convention générateur, la tension aux bornes du générateur réel est alors

La f.é.m. est aussi appelée tension à vide et on parle de résistance de sortie, ou de résistance interne pour désigner $r$.

La résistance de sortie d’un générateur de tension continue est inférieure à $1 \Omega$, tandis que celle d’un générateur de tension alternatif ( GBF : générateur basse fréquence) est de $50 \Omega$.