Titre à compléter - Livre chapeau

Application 1:

Ligne haute tension → électrolyse des sels → ions.

V_{A B}+V_{B C}=V_{A}-V_{B}+V_{B}-V_{C}=V_{A}-V_{C}=V_{A C}

(1)

Application 2: 1)

\begin{aligned} & I_{2}=I_{0}-I_{1}=4-1=3 \mathrm{~A} \\ & I_{5}=I_{2}-I_{4}=3-2=1 \mathrm{~A} \\ & I_{3}=I_{1}+I_{5}=2 \mathrm{~A} \end{aligned}

(2)

Exercice à résoudre:

\text { 2) } \begin{aligned} & I=\delta a \\ & q=e \times e^{-} \\ & I=e \frac{e^{-}}{\delta t} \\ & I==\frac{1}{\partial t} \\ & \text { Pour }+=+\frac{I}{e}=2=2, I \times 10^{\frac{1}{2}} \end{aligned}

(3)

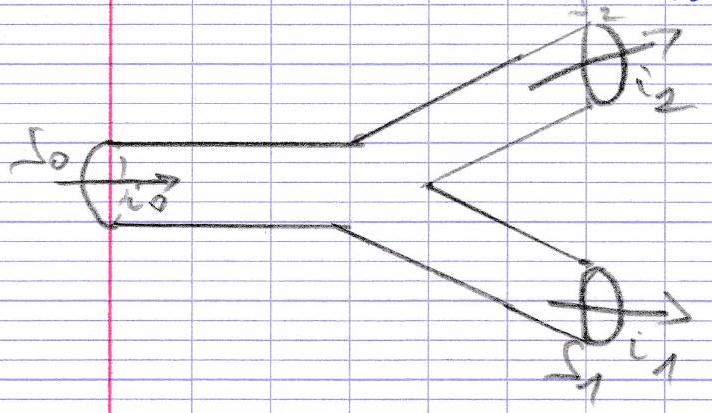
Pendant dt: charge sortante par $J_{1} \rightarrow d q_{1}$ Charge portée par $S_{2} \rightarrow d q_{2}$ Charge entrante par $s_{0} \rightarrow d_{0}$ Par conservation de la charge dans CARQS, pas d’accumulation de charges. Donc le nombre de charges entrantes doit être égal au nombre de charges sortantes pendant dt: $d q_{0}=d q_{1}+d q_{2} \Rightarrow \frac{d q_{0}}{d t}=\frac{d q_{1}}{d t}+\frac{d q_{2}}{d t} \Rightarrow i_{0}=i_{1}+i_{2}$

Applicationa:

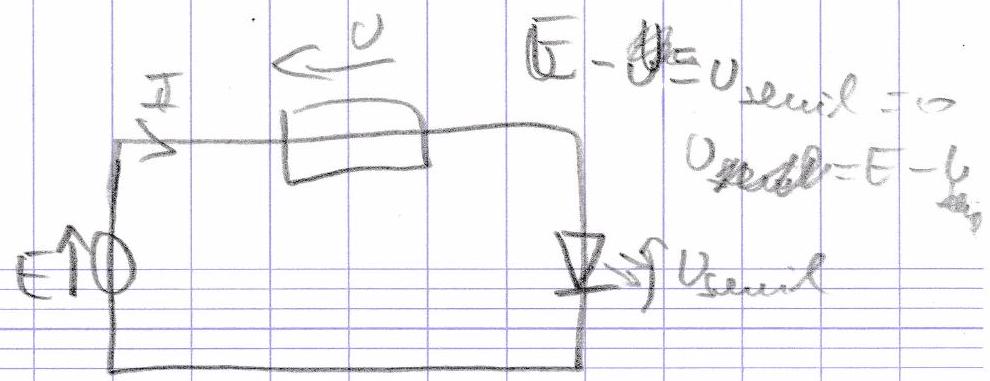
\begin{aligned} & E=U_{1} U_{2}=0 \\ & U_{2}=-U_{1}+E=+5=-M_{2} V \\ & E-U_{1}+U_{3}-U_{4}=0 \\ & U_{3}=-E+U_{1}+U_{4}=-5+3+1=-1 U \\ & U_{1}=V_{A}-V_{B} \quad U_{3}=V_{B}-V E \quad E=V_{M}-V_{A} \\ & U_{1}+U_{3}=V_{A}-V_{C} \quad E=0-V_{A} \\ & V_{C}=-5-U_{1}-U_{3}=-5=-5=-5=-5 \end{aligned}

(4)

Application 4:

lompe: t cadiateur:- Eintale nuteris:Abouterio des provar tphowe:t
convention retepteur 1 retepteur, siciptater 3) $P=\frac{\Delta E}{\Delta t} \quad \Delta E=P \times \Delta F$

A N: \Delta E=1 \times 10^{3} \times 1 \times 3600=3,6 \times 10^{6} \mathrm{~J}

(5)

Application 5

$1 \mid U=R I$ aver Exam & $I=I_{\text {max }}$ $R=\frac{E-V_{\text {sevil }}}{I_{\text {max }}}$ AN: $R=\frac{5-2}{20 \times 10^{-3}}=0$ then $15 \times 10^{2} \Omega$ $21 \rho=2 r^{0} \times 20 \times 10^{-3}=4,0 \times 10^{-2} \mathrm{~W}$ 3) Onsait que $P-V=: x I_{\text {max }}$

Or d’Opeí la loi d’ohm $U = RX I_{\text{max}}$ $\operatorname{Danc} P=\frac{\mho^{2}}{\dot{R}} \quad A N: P=6,0 \times 10^{-2} \mathrm{~W}$ On>ait que $P=U \times I_{\text {max }}$ Or d’ouplès la loi d’ohm $V=R \times I_{\text {max }}$ Dome $P=R \times I^{2}$ moy Exercic de cours à commonte? 4)

\begin{gathered} U_{R_{1}}=R_{1} \times I \\ U_{R_{2}}=R_{2} \times I \\ O_{1} U_{R}=U_{R_{2}} \times U_{R_{1}} \\ U_{R}=I \times\left(R_{1}+R_{2}\right) \\ U R=R_{21} \times I \\ R_{21}=R_{1}+R_{2} \end{gathered}

(6)

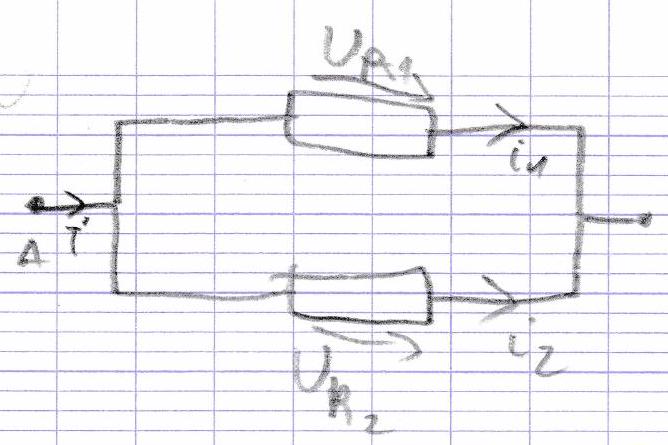
\begin{gathered} U_{R_{1}}=R_{1} \times i_{1} \\ U_{R_{2}}=R_{2} \times i_{2} \\ i=\frac{U_{R_{2}}}{R_{2}}+\frac{U R_{1}}{R_{1}} \\ i=\frac{U_{R}}{R_{\text {iq }}} \frac{U_{R}}{R_{\text {iq }}}=\frac{U_{R_{2}}}{R_{2}}+\frac{U R_{1}}{R_{1}} \\ O r U_{R}=U_{R_{2}}=U_{R_{1}} \\ \text { Dam } \\ \text { Dam }=\frac{1}{R_{\text {iq }}}=\frac{1}{R_{2}}+\frac{1}{R_{1}} \end{gathered}

(7)

Application 6