Chapitre 1¶

Modèle de l’optique géométrique¶

Plus de 38 millions de foyers français peuvent recevoir maintenant l’internet très haut débit par fibre optique. Quel phénomène permet de transmettre l’information à l’aide de fibres optiques sur plusieurs centaines de kilomètres? La fibre optique est également utilisée dans le domaine médical, par exemple dans les fibroscopes.

Dans ce chapitre et le suivant, on s’intéressera à la modélisation géométrique de la propagation de la lumière et à l’utilisation de la notion de rayon lumineux.

I) Description de la lumière¶

A ) Nature de la lumière¶

Au XVIIIe siècle, deux modèles décrivant la nature de la lumière s’opposaient : Newton affirmait que les objets lumineux émettaient des corpuscules obéissant aux lois de la mécanique, tandis que Huygens affirmait que la lumière était une onde.

La renommée de Newton, liée à ses travaux sur la gravitation, a permis à la théorie corpusculaire de s’imposer parmi les scientifiques de l’époque. Mais au début du XIXe siècle, les expériences d’interférences et de diffraction de Fresnel et Young ont un temps permis d’imposer le modèle ondulatoire de la lumière. À la fin du XIXe siècle, les travaux de Planck, sur le corps noir notamment, ont remis en question le modèle ondulatoire de la lumière.

Aujourd’hui, la lumière est décrite de manière complète par les deux modèles : le modèle corpusculaire (photon) et le modèle ondulatoire (onde électromagnétique). On parle de dualité onde-corpuscule (cf. chapitre ultérieur). Ces deux modèles permettent d’expliquer l’ensemble des expériences réalisées jusqu’à maintenant avec la lumière.

B) Spectre de la lumière¶

La lumière fait partie d’un ensemble plus vaste d’ondes appelées ondes électromagnétiques. Ces ondes (et donc a fortiori la lumière) sont caractérisées par une double périodicité : temporelle et spatiale. Le spectre peut donc être représenté en fonction de la fréquence ou de la longueur d’onde.

Rappel¶

Pour une onde de fréquence $f$ qui se propage à la vitesse $v$ , la longueur d’onde $\lambda$ est donnée par :

\lambda=\frac{c}{f}

(1)

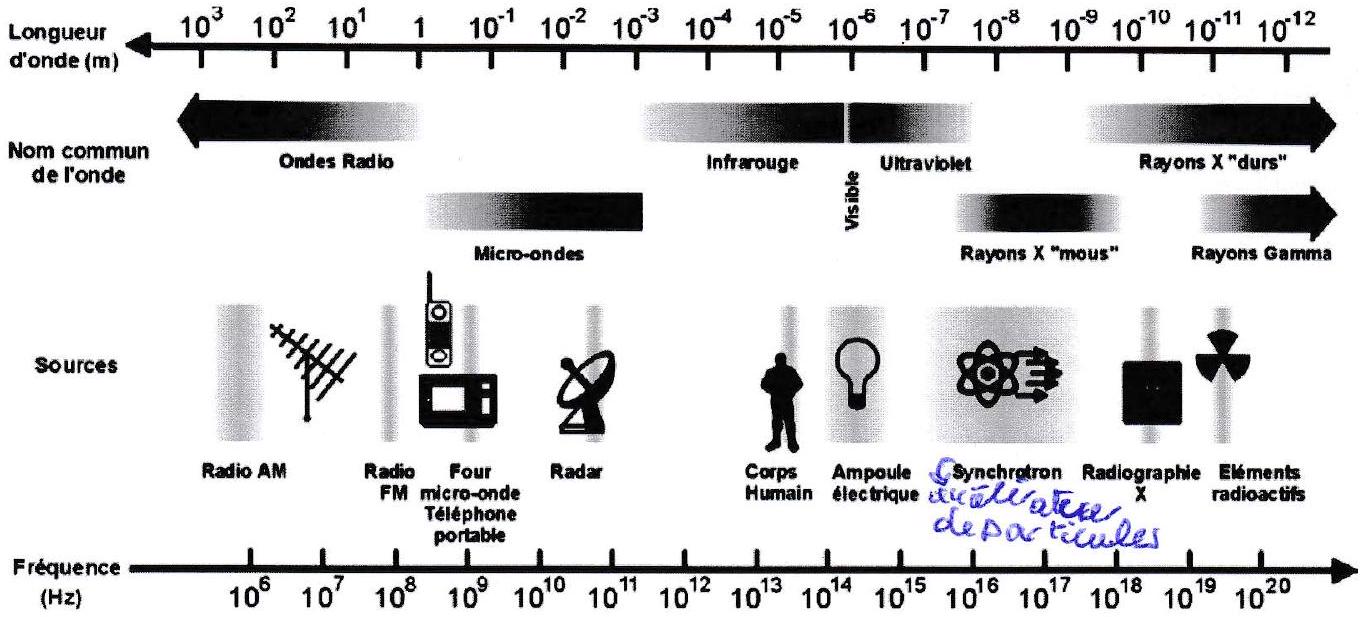
Figure 1.1: Spectre Électromagnétique

La lumière visible a un spectre constitué de longueurs d’onde dans le vide situées entre 400 nm (violet) et 800 nm (rouge), c’est-à-dire de fréquences comprises entre $4 \cdot 10^{14} \mathrm{~Hz}$ (rouge) et $8 \cdot 10^{14} \mathrm{~Hz}$ (violet). Le tableau ci-dessous donne quelques valeurs approchées de longueurs d’onde dans le vide associées à une couleur du spectre :

Couleur	bleu	vert	jaune	rouge
$\lambda_{\mathbf{0}}(\mathbf{n m})$	$450-500$	$500-550$	$550-600$	$650-800$

C ) Propagation de la lumière¶

1) Dans le vide¶

La lumière se propage dans le vide avec une vitesse indépendante de la fréquence et du référentiel d’étude.

La lumière se propage dans le vide avec une vitesse constante $c$ de valeur

c=3,00 \cdot 10^{8} \mathrm{~m} \cdot \mathrm{~s}^{-1}

(2)

2 ) Dans un milieu transparent¶

Définition 1 : Milieu transparent¶

Un milieu est qualifié de transparent lorsqu’il n’absorbe pas d’énergie lumineuse. Dans un milieu transparent, la lumière se propage à une vitesse $v$ inférieure à la vitesse $c$ de la lumière dans le vide. Afin de quantifier cette diminution, on introduit l’indice optique $n$ du milieu.

Définition 2 : Indice optique¶

L’indice optique (ou indice de réfraction) $n$ d’un milieu est défini par le rapport de la vitesse $c$ de la lumière dans le vide sur la vitesse $v$ de la lumière dans ce milieu :

n=\frac{c}{v}

(3)

Exemple¶

Voici quelques ordres de grandeurs de l’indice optique :

$n($ vide $)=1$ ;
$n(\mathrm{air})=1,00029 \simeq 1$ ;
$n(\mathrm{eau})=1,33 ;$
$n($ verre $)=1,5$ .

Remarque¶

On note que :

par définition, l’indice optique est nécessairement supérieur ou égal à 1 ;
l’indice optique varie avec les conditions physiques du milieu (pureté, pression, . . . );
l’indice optique peut aussi varier en fonction de la fréquence de la lumière. On parle alors de milieu dispersif.
Pour deux milieux d’indice optique respectif $n_{1}$ et $n_{2}$ , si $n_{2} \ngtr n_{1}$ on dit milieu d’indice $n_{1}$ est moins réfringent que le milieu d’indice $n_{2}$ .

La fréquence de la lumière ne dépend pas du milieu matériel étudié. Par conséquent, la modification de la vitesse de la lumière dans un milieu d’indice optique $n$ engendre une modification de la longueur d’onde.

Dans un milieu d’indice optique $n$ , la longueur d’onde $\lambda$ est reliée à celle dans le vide $\lambda_{0}$ par :

\lambda=\frac{\lambda_{0}}{n}

(4)

exager de etranver la formule

Remarque¶

Il faut donc toujours bien spécifier le milieu dans lequel se fait l’étude.

II ) Les sources lumineuses¶

Différents objets peuvent servir de source primaire en optique, ils diffèrent par le spectre émis, la puissance émise ainsi que la directivité de la lumière.

A) Source thermique¶

Tout corps de température non nulle émet un rayonnement thermique induit par le mouvement continu et désordonné des particules qui le constituent. Ce rayonnement est caractérisé par un spectre continu et large et possédant un maximum à une longueur d’onde précise dépendant de la température du corps.

On remarque que plus la température du corps augmente, plus le maximum en intensité se déplace vers les longueurs

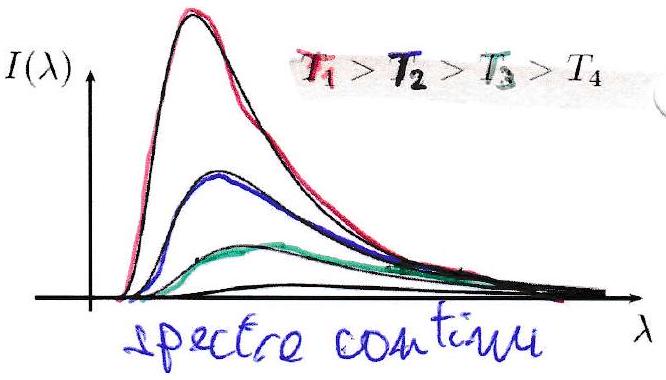
d’onde faibles.

Une source thermique fonctionne à partir du rayonnement thermique émis par un corps chauffé. Le spectre d’une source thermique est un spectre continu. effet jould : electricité passant dans unfil → invagia → chalur → buming Exemple Soleil, lampe à incandescence, lampe halogène, corps humain.

B ) Source spectrale¶

Cé sont des lampes dont le principe repose sur les transitions électroniques d’un atome ou d’une molécule en phase gaz. Lorsqu’un électron se désexcite, il émet une radiation lumineuse de longueur d’onde bien définie. Leur spectre est un spectre de raies correspondant aux différentes transitions électroniques possibles.

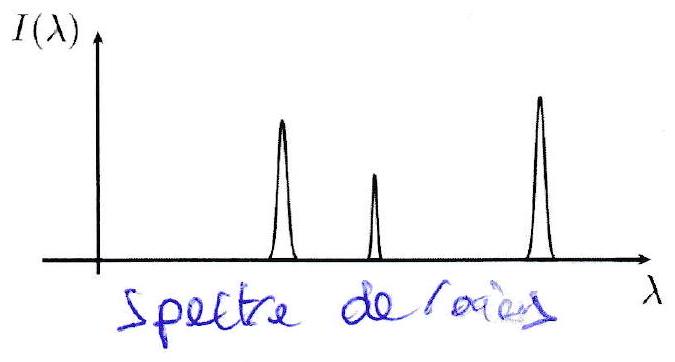
Une source spectrale émet un rayonnement discontinu constitué de plusieurs fréquences précises. Le spectre est discret et contient des pics fins appelés raies spectrales.

C ) Sources LASER¶

Une source LASER (Light Amplification by Stimulated Emission of Radiation) fonctionne sur le même principe que les lampes spectrales, à la différence près que le dispositif fait en sorte de désexciter tous les atomes en même temps.

Le rayonnement émis effectue alors des allers-retours entre plusieurs miroirs, permettant ainsi d’amplifier son intensité

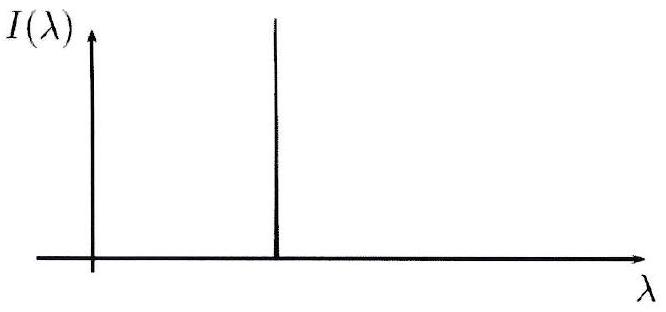
et de sélectionner une seule fréquence donnée (cf. chapitre ultérieur).

Dans une source LASER, le spectre est donc discontinu et ne contient qu’une seule fréquence. Le danger des LASER vient de leur grande puissance surfacique.

Le spectre d’un faisceau LASER présente une unique raie spectrale beaucoup plus fine qu’une raie de lampe spectrale.

D) Modèle de la source ponctuelle monochromatique¶

Dans la suite, nous utiliserons le modèle de la source ponctuelle et monochromatique :

source ponctuelle $(\neq$ étendue $)=$ la source est un point de l’espace. Ce point envoie des rayons dans toutes les directions.
source monochromatique ( $\neq$ polychromatique) $=$ le spectre ne contient qu’une seule radiation monochromatique (une seule raie spectrale).

Une source étendue peut être découpée en une assemblée de sources quasi ponctuelles qui émettent indépendamment les unes des autres. Une source polychromatique peut être décomposée en sources quasi monochromatiques.

Remarque¶

Les sources ponctuelles ou monochromatiques sont des modèles théoriques qui n’ont pas de réalité physique. La source LASER constitue la forme la plus proche du modèle de la source lumineuse monochromatique.

III ) Modèle de l’optique géométrique¶

A) Cadre de l’approximation de l’optique géométrique¶

L’optique géométrique est applicable lorsque les effets ondulatoires peuvent être ignorés.

Approximation de l’optique géométrique¶

Dans le cadre de l’optique géométrique, on néglige tous les phénomènes de diffraction. Pour cela, les tailles $d$ des instruments d’optique utilisés (par exemple diamètre d’une lentille) devront être très grandes devant la longueur d’onde $\lambda: d \gg \lambda(d>1000 \lambda)$ .

B ) Notion de rayon lumineux¶

Dans le cadre de l’optique géométrique, la propagation de l’énergie lumineuse est décrite à l’aide de la notion de rayons lumineux.

Rayons lumineux¶

Les rayons lumineux vérifient les propriétés suivantes :

Principe du retour inverse de la lumière : Le trajet suivi par la lumière entre deux points situés sur le même rayon lumineux est indépendant du sens de propagation de la lumière.

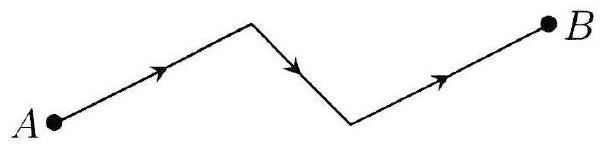
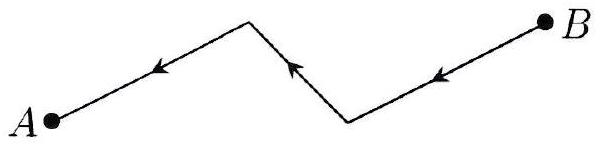
Indépendance des rayons lumineux : Il n’y a pas de phénomènes d’interférences, les rayons lumineux qui se croisent n’interagissent pas entre eux, ils se propagent de façon entièrement indépendante.

Remarque¶

Limite du modèle : Les rayons lumineux sont un modèle qui permet de décrire la propagation de l’énergie lumineuse dans le cadre de l’optique géométrique, mais il est bien évident qu’en réalité la lumière ne se présente pas sous la forme de rayons infiniment fins. En effet, la diffraction empêche de limiter autant qu’on le souhaite la section des faisceaux lumineux. Il est donc impossible d’isoler un seul rayon lumineux.

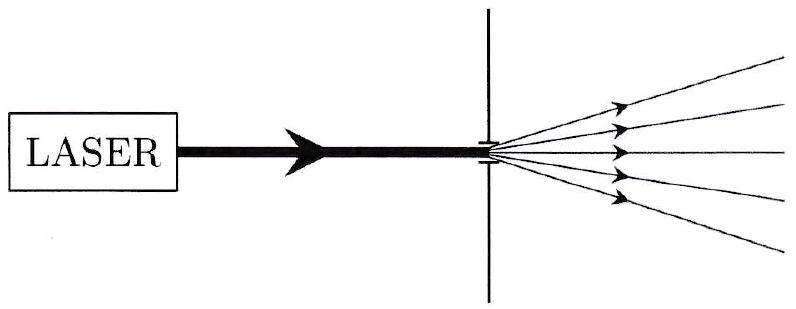
Diaphragme

Remarque¶

Le faisceau LASER, très directif, est proche du modèle du rayon lumineux.

C) Propagation rectiligne de la lumière¶

Dans le vide, la lumière se propage de façon rectiligne. Cependant, ce n’est a priori pas le cas dans n’importe quel milieu matériel.

Il existe des milieux particuliers où la lumière se propage rectilignement : il s’agit des milieux transparents, linéaires, homogènes et isotropes (MTLHI).

Définition 3 : MTLHI¶

transparents : ils n’absorbent pas d’énergie lumineuse;
linéaires : il n’y a pas de modification de la fréquence de l’onde au cours de la propagation;
homogènes : les propriétés physiques (température, masse volumique, indice de réfraction) sont identiques en tout point;
isotropes : les propriétés physiques sont identiques dans toutes les directions de l’espace (pas de direction privilégiée).

La lumière se propage en ligne droite dans un milieu transparent homogène et isotrope.

Remarque¶

Lorsque le milieu n’est pas homogène, notamment lorsque l’indice optique varie avec la température, la lumière ne se propage plus en ligne droite. Cela explique par exemple les mirages optiques observés dans les milieux où la température varie fortement en fonction de l’altitude (désert, zone glaciaire, ...).

Dans la suite de ce chapitre, nous considérerons uniquement des milieux transparents, linéaires, homogènes et isotropes (MTLHI).

IV ) Lois de Snell-Descartes¶

Lorsqu’il y a un changement de milieu, la lumière ne se propage plus de façon rectiligne mais en suivant les lois de Snell-Descartes.

A ) Vocabulaire¶

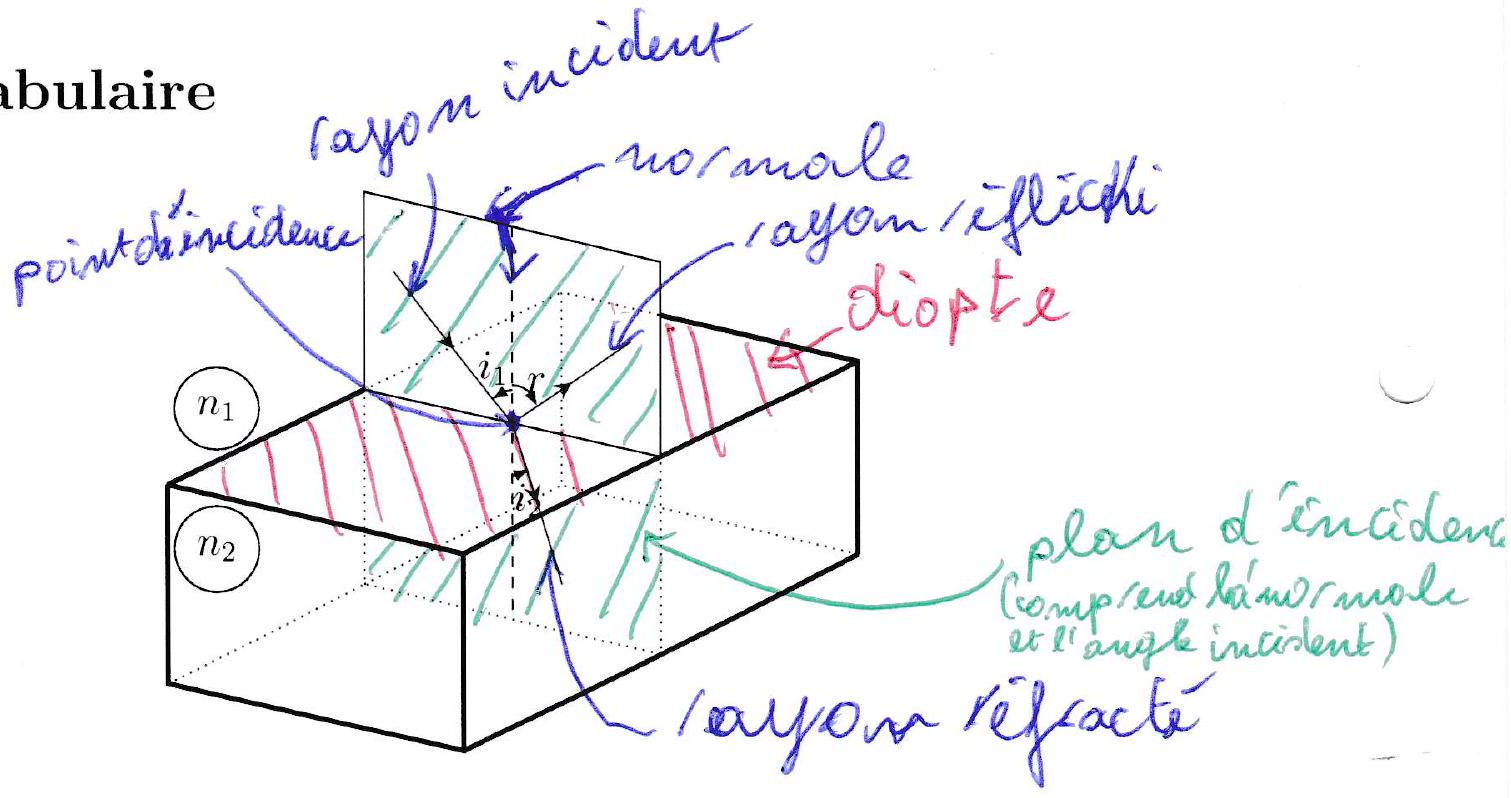
Définition 4 :¶

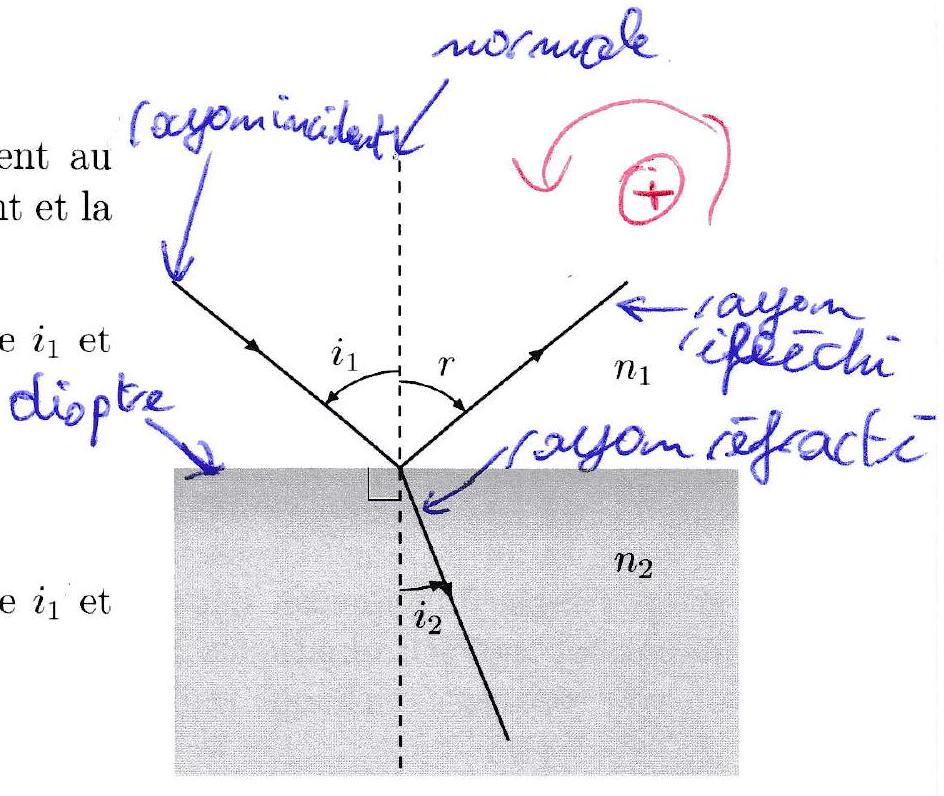
Dioptre : l’interface séparant deux milieux transparents d’indices différents est appelée un dioptre;
Rayon incident : le rayon arrivant sur le dioptre est appelé rayon incident;
Rayon réfléchi et rayon réfracté : lorsqu’un rayon lumineux arrive sur un dioptre, ce rayon donne naissance à un rayon réfléchi qui repart dans le milieu que le rayon incident et à un rayon réfracté qui se propage dans l’autre milieu;
Point d’incidence : le point I où le rayon incident rencontre le dioptre est appelé point d’incidence;
Normale: la droite perpendiculaire au dioptre, au point où le rayon incident rencontre le dioptre (point d’incidence), est appelée la normale au dioptre;
Plan d’incidence : le plan contenant la normale et le rayon incident est appelé plan d’incidence.
Les angles $i_{1}, r$ et $i_{2}$ sont respectivement appelés angle d’incidence, angle de réflexion et angle de réfraction.

Définition 5 : Angles orientés¶

En optique, les angles sont définis ALGÉBRIQUEMENT à partir de la normale :

les angles sont positifs pour une rotation dans le sens trigonométrique;
les angles sont négatifs pour une rotation dans le sens horaire.

B ) Énoncé des lois¶

On note $n_{1}$ l’indice optique du milieu de propagation du rayon incident et $n_{2}$ l’indice optique du milieu de propagation du rayon réfracté.

Lois de Snell-Descartes¶

Les rayons réfléchi et réfracté appartiennent au plan d’incidence (défini par le rayon incident et la normale au point d’incidence).
Loi de la réflexion : L’angle d’incidence $i_{1}$ et l’angle de réflexion $r$ sont opposés.

i_{1}=-r

(5)

Loi de la réflexion : L’angle d’incidence $i_{1}$ et de réfraction $i_{2}$ sont reliés par :

n_{1} \sin \left(i_{1}\right)=n_{2} \sin \left(i_{2}\right)

(6)

Remarque¶

ATTENTION :¶

Le premier point est aussi important que les points suivants donnant les relations entre les angles.
L’énoncé des lois de Snell-Descartes doit s’accompagner d’un schéma complet sur lequel toutes les notations sont introduites.
Les rayons réfléchi et réfracté sont de l’autre côté de la normale par rapport au rayon incident.

Remarque¶

Principe de Fermat : la lumière se propage d’un point à un autre sur des trajectoires telles que la durée du parcours soit minimale. Le phénomène de réfraction résulte du fait que la vitesse de propagation est différente dans les deux milieux.

C) Détails sur la réfraction¶

Exercice de cours à connaître 1¶

Que se passe-t-il si le rayon incident arrive selon la normale?
Comparer les angles de réfraction et d’incidence selon les valeurs respectives des deux indices de réfraction ( $n_{2}<n_{1}$ puis $n_{2}>n_{1}$ ).

Application 1¶

Un rayon lumineux dans l’air tombe sur la surface de l’eau d’indice 1,33.

Déterminer l’angle de réfraction pour un angle d’incidence de $30^{\circ}$ .
Déterminer l’angle d’incidence pour un angle de réfraction de $30^{\circ}$ .

D ) L’arc-en-ciel (culture)¶

L’indice optique des milieux transparents dépend de la fréquence de la lumière : on dit que le milieu est dispersif.

D’après la loi de Snell-Descartes, l’angle de réfraction, qui dépend de l’indice optique du milieu et de l’angle d’incidence, dépend également de la fréquence de la lumière.Alors, les différentes radiations monochromatiques ne sont pas déviées avec le même angle, ce qui disperse la lumière : on voit séparément chaque radiation monochromatique.

C’est ce phénomène qui vous a permis d’observer les spectres avec des prismes au lycée et qui est à l’origine des arcs-en-ciel.

E ) Réflexion totale¶

Exercice de cours à connaître 2¶

Lorsque la lumière passe d’un milieu 1 à un milieu 2 moins réfringent ( $n_{2}<n_{1}$ ), que se passe-t-il si l’angle d’incidence $i_{1}$ “devient trop grand” ? (cf. animation)
Déterminer l’angle d’incidence limite $i_{1, \text { lim }}$ au-delà duquel il n’existe plus de rayon réfracté. Que devient alors l’énergie lumineuse? Ce phénomène s’appelle la réflexion totale.

Condition de réflexion totale¶

Pour avoir réflexion totale, le rayon réfracté ne doit pas exister. Pour cela, il faut :

que le rayon lumineux se propage d’un milieu plus réfringent à un milieu moins réfringent (deuxième milieu d’indice plus faible que le premier);
ET que l’angle d’incidence soit supérieur à l’angle d’incidence limite obtenu pour un angle de réfraction égal à $\pi / 2$ .

Application 2¶

Dans le cas du dioptre air-eau, déterminer les conditions pour avoir réflexion totale. On donne : $n_{\text {air }}=1,00$ et $n_{\text {eau }}=1,33$ .

V ) La fibre optique à saut d’indice¶

A ) Description¶

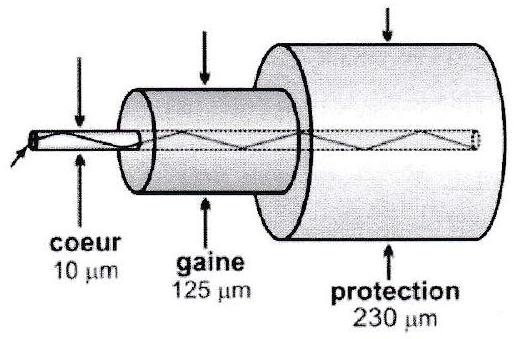
Le guidage de la lumière peut être assuré par des fibres optiques. Une fibre optique à saut d’indice est constituée d’un cylindre de verre (ou de plastique) appelé cœur ou âme, LTHI(linéaire, transparent, homogène, isotrope) d’indice $n_{1}$ et de rayon $R$ , entouré d’une gaine transparente d’indice optique $n_{2}$ . La gaine contribue non seulement aux propriétés mécaniques de la fibre mais évite aussi les fuites de lumière vers d’autres fibres en cas de contact. Actuellement, le diamètre du cœur d’une fibre varie de 3 à $200 \mu \mathrm{~m}$ selon les propriétés et le diamètre extérieur de la gaine peut atteindre $400 \mu \mathrm{~m}$ . La gaine est entourée par un matériau protecteur (plastique en général) pour atteindre un diamètre total de l’ordre du millimètre.

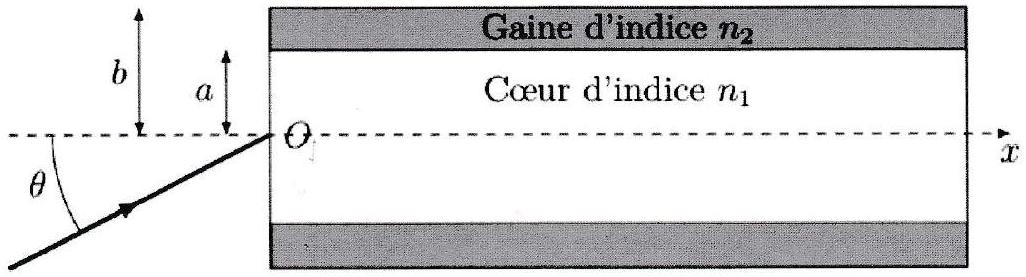
Les faces d’entrée et de sortie sont perpendiculaires à l’axe ( $O x$ ) du cylindre formé par la fibre. L’ensemble, en particulier la face d’entrée, est en contact avec un milieu d’indice $n_{0}$ . On s’intéresse à la trajectoire d’un rayon lumineux situé dans le plan de symétrie contenant l’axe ( $O x$ ).

B ) Vocabulaire¶

La fibre à saut d’indice doit permettre de guider les rayons lumineux de sa face d’entrée vers sa face de sortie en minimisant les pertes.

Définition 6 : Cône d’acceptance¶

Le cône d’acceptance d’une fibre optique est le cône à l’intérieur duquel les rayons incidents seront guidés par réflexion totale interne. Tout rayon lumineux appartenant au cône d’acceptance c’est-à-dire faisant un angle $\theta$ avec la normale à la face d’entrée tel que $-\theta_{\text {max }}<$ $\theta<\theta_{\text {max }}$ , subira alors des réflexions successives totales sur le dioptre cœur/gaine. $\theta_{\text {max }}$ est appelé angle d’acceptance. On définit l’ouverture numérique $n_{0} \sin \left(\theta_{\max }\right)$ où $n_{0}$ est l’indice optique du milieu d’où provient le rayon incident et $\theta_{\text {max }}$ l’angle d’acceptance.

Définition 7 : Dispersion intermodale¶

Les rayons parvenant dans la fibre avec des angles d’incidence différents suivent des chemins optiques (ou modes) différents. À chaque mode correspond un temps de parcours légèrement différent, ce qui entraîne une dispersion intermodale. On définit le retard intermodal comme le temps de retard à l’arrivée du rayon le plus lent (le plus incliné) par rapport au rayon le plus rapide (rayon axial) :

\Delta t=t_{\max }-t_{\min }

(7)

C ) Application¶

Exercice de cours à connaître 3¶

Quel phénomène physique permet de guider la lumière dans la fibre, sans perte d’énergie au cours du parcours ? Comment doit-on alors choisir $n_{1}$ et $n_{2}$ ?En supposant que cette condition est remplie, faire un schéma du trajet d’un rayon à travers la fibre, en représentant plusieurs réflexions sur l’interface cœur/gaine.

Cône d’acceptance¶

Établir lạ condition sur l’angle d’incidence sur le dioptre cœur/gaine pourqu’il s’y produise une réflexion totale.
En déduire une condition sur l’angle de réfraction au niveau du dioptre air/cœur.
En déduire que ce rayon peut être guidé dans le cœur si le rayon incident parvient dans le cône d’acceptance d’angle d’acceptance $\theta_{\text {max }}$ qui vérifie

O N=n_{0} \sin \left(\theta_{\max }\right)=\sqrt{n_{1}^{2}-n_{2}^{2}}

(8)

On donne : $\sin (\arccos (x))=\sqrt{1-x^{2}}$ et cos $(\arcsin (x))=\sqrt{1-x^{2}}$ . 5. Faire l’application numérique pour : $n_{1}=1,500$ et $n_{2}=1,489$ .

Dispersion intermodale¶

Une impulsion lumineuse arrive à $t=0$ , au point O sur la fibre précédente de longueur $L$ , sous la forme d’un faisceau conique convergent d’axe ( $O x$ ) et de demi-angle au sommet $\theta_{i}<\theta_{\text {max }}$ .

Quel rayon a la durée de parcours la plus courte ? Déterminer cette durée $t_{\text{min}}$ minimale en fonction de $L, n_{1}$ et $c$ .
Quel rayon a la durée de parcours la plus longue ? Déterminer cette durée $t_{\text{max}}$ maximale en fonction de $L, n_{1}, c$ et $\theta_{i}$ .
Calculer le retard intermodal $\Delta t$ de cette impulsion à la sortie de la fibre, avec $L=10 \mathrm{~m}$ et $\theta_{i}=8^{\circ}$ .