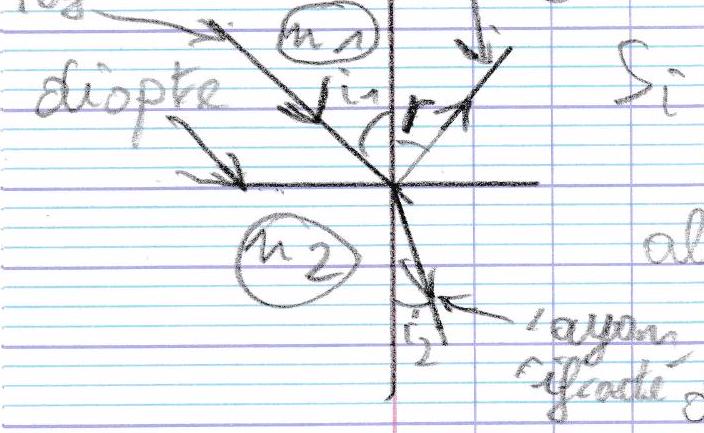
Exercice de cours à compléter
Exercice de cours à compléter ¶ − i 1 = 0 r = 0 -i_{1}=0 \quad r=0 \quad − i 1 = 0 r = 0 m 1 sin ( i 1 ) = 0 m_{1} \sin \left(i_{1}\right)=0 m 1 sin ( i 1 ) = 0 n 2 sin ( i 2 ) = 0 n_{2} \sin \left(i_{2}\right)=0 n 2 sin ( i 2 ) = 0 ( − 1 ) ≤ i n ( i 2 ) = 0 (-1) \leq i n\left(i_{2}\right)=0 \quad ( − 1 ) ≤ in ( i 2 ) = 0 12 = 0.00 π 12=0.00 \pi 12 = 0.00 π L = x L=x L = x
n 2 sin ( i 2 ) = m n sin ( i 1 ) \quad n_{2} \sin \left(i_{2}\right)=m_{n} \sin \left(i_{1}\right) n 2 sin ( i 2 ) = m n sin ( i 1 )
wormal ¶ roy on wercident
sin ( i 2 ) sin ( i 1 ) = m 1 m 2 \frac{\sin \left(i_{2}\right)}{\sin \left(i_{1}\right)}=\frac{m_{1}}{m_{2}} sin ( i 1 ) sin ( i 2 ) = m 2 m 1 n 2 < n 1 n_{2}<n_{1} n 2 < n 1
alors 1 < n 1 n 2 1<\frac{n_{1}}{n_{2}} 1 < n 2 n 1
dom sin ( i 2 ) sin ( i 1 ) > 1 Fen sin ( 1 2 ) > sin ( in ′ ) domi iz > is ω 0 < i 2 < Γ 2 μ α i 1 < Γ 2 μ sin ( x ) croilsante aur [ 0 ; π 2 ] si n 2 > n 1 alon 1 > n 1 n 2 dom ( tin ( i 2 ) tin ( i 1 ) > α ( = 1 sin ( i 2 ) > sin ( i 1 ) \begin{aligned}
& \operatorname{dom} \frac{\sin \left(i_{2}\right)}{\sin \left(i_{1}\right)}>1 \\
& \text { Fen } \sin \left(\frac{1}{2}\right)>\sin \left(\text { in }^{\prime}\right) \\
& \text { domi iz }>\text { is } \\
& \omega_{0}<i_{2}<\frac{\Gamma}{2} \quad \mu \alpha i_{1}<\frac{\Gamma}{2} \quad \mu \sin (x) \\
& \text { croilsante aur }\left[0 ; \frac{\pi}{2}\right] \\
& \text { si } n_{2}>n_{1} \\
& \text { alon } 1>\frac{n_{1}}{n_{2}} \\
& \operatorname{dom}\left(\frac{\operatorname{tin}\left(i_{2}\right)}{\operatorname{tin}\left(i_{1}\right)}>\alpha\left(=1 \sin \left(i_{2}\right)>\sin \left(i_{1}\right)\right.\right.
\end{aligned} dom sin ( i 1 ) sin ( i 2 ) > 1 Fen sin ( 2 1 ) > sin ( in ′ ) domi iz > is ω 0 < i 2 < 2 Γ μα i 1 < 2 Γ μ sin ( x ) croilsante aur [ 0 ; 2 π ] si n 2 > n 1 alon 1 > n 2 n 1 dom ( tin ( i 1 ) tin ( i 2 ) > α ( = 1 sin ( i 2 ) > sin ( i 1 ) Doni in nivisite plus C’est ex phinamine de seflexion tatale?
D’apres la bei de snell-Descorter:
u 1 sin ( i 1 ) = m 2 → u_{1} \sin \left(i_{1}\right)=m_{2} \rightarrow u 1 sin ( i 1 ) = m 2 →
On a xurtin n n 2 < n n_{2}<n n 2 < n
i 2 = π 2 v i_{2}=\frac{\pi}{2} v i 2 = 2 π v i k n = sin − 1 ( n 2 n 1 ) i_{k_{n}}=\sin ^{-1}\left(\frac{n_{2}}{n_{1}}\right) i k n = sin − 1 ( n 1 n 2 )
Vrain car m 2 m 1 < 1 \frac{m_{2}}{m_{1}}<1 m 1 m 2 < 1
Iflexion
totale sirit > i.evon