Mathématiques - PCSI¶

Rudiments de logique
ET VOCABULAIRE ENSEMBLISTE¶

Lycée Lakanal 3 avenue du Pdt Franklin Roosevelt 92330 Sceaux

8 Rudiments de logique et vocabulaire ensembliste.¶

8.1 Disjonction, conjonction, négation.¶

Une assertion en mathématique est un énoncé dont on peut dire s’il est vrai ou s’il est faux. Aux énoncés vrais, on assigne la valeur 1 et aux énoncés faux, on assigne la valeur 0 .

En mathématiques, une assertion vraie porte le nom de proposition et selon l’importance de cette proposition au sein de la théorie, elle pourra porter le nom de théorème, corollaire, lemme,...

Conjonction.¶

Soient $p, q$ deux assertions. Les valeurs logiques prises par l’énoncé « $p$ ET $q$ » sont résumées dans la table de vérité

L’assertion $p \mathrm{ET} q$ est donc l’énoncé mathématique qui est vrai dans le seul cas où $p$ et $q$ sont simultanément vrais.

Disjonction.¶

Soient $p, q$ deux assertions. Les valeurs logiques prises par l’assertion < $p$ OU $q$ » sont résumées dans la table de vérité

L’assertion $p$ OU $q$ est donc l’énoncé mathématique qui est faux dans le seul cas où $p$ et $q$ sont simultanément faux. Autrement dit, $p$ OU $q$ est vrai dès que l’un au moins des énoncés $p$ ou $q$ est vrai.

Remarque. En logique mathématique, l’assertion « $p$ OU $q$ » n’exprime pas que $p$ et $q$ s’excluent mutuellement: « $p$ OU $q$ » ne dit pas que l’on ne peut avoir à la fois $p$ et $q$. En géométrie, un triange isocèle est un triangle ayant deux côtés égaux ou deux angles égaux : il est impossible ici que le ou soit exclusif. Une fonction monotone est une fonction croissante ou décroissante : les fonctions constantes sont monotones et elles sont à la fois croissantes et décroissantes.

Propriété. Soient $p, q$ et $r$ trois assertions. On a les propriétés de distributivité suivantes :

Négation.¶

Soit $p$ une assertion. Les valeurs logiques prises par la négation de $p$ sont résumées dans la table de vérité :

L’assertion NON $-p$ est vraie dans le seul cas où l’assertion $p$ est fausse. Remarques. (1) NON $-(\mathrm{NON}-p)=p$ (2) L’assertion ( $\mathrm{NON}-p$ ) OU $p$ est vraie, quelle que soit l’assertion $p$ : c’est le principe du tiers exclu. (3) L’assertion ( NON $-p$ ) ET $p$ est fausse, quelle que soit l’assertion $p$ : c’est le principe de non contradiction.

Lois de De Morgan. Soient $p$ et $q$ deux assertions. La négation de l’assertion « $p$ ET $q$ » est l’assertion « ( $\mathrm{NON}-p$ ) $\mathrm{OU}(\mathrm{NON}-q)$ ». La négation de l’assertion «p OU $q$ » est l’assertion « ( NON $-p$ ) ET ( NON $-q$ )».

Exercice 1. Soient $a, b, c$ trois réels. Quelle est la négation de $a=b=c$ ? Quelle est la négation de $a \leq b \leq c$ ?

Exercice 2. Résoudre dans $\mathbb{R}^{2}$ le système $\left\{\begin{array}{l}(x-1)(y-2)=0 \\ (x-3)(y-1)=0\end{array}\right.$

Implication et équivalence¶

Dans le langage courant, on formule une implication à l’aide des mots «si, alors» et la connexion entre les propositions jointes n’est pas toujours facile à caractériser. Souvent, il s’agit d’une cause qui implique une conséquence comme dans «s’il pleut alors le sol est mouillé. » Les implications du langage courant sont ainsi plus restreintes.

En logique mathématique, une implication est un énoncé obtenu en joignant deux assertions sans qu’il existe une forme de connexion «psychologique» entre elles, et dont la valeur logique dépend exclusivement de celles des assertions mises en relation. On exclut en mathématique, que d’une assertion vraie il puisse découler une assertion fausse et on pose donc qu’une implication mathématique «si $p$ alors $q$ » est fausse dans le seul cas où « $p$ est vraie et $q$ est fausse. »

Implication. Etant donnés deux assertions $p, q$, l’implication de $q$ par $p$ notée $p \rightarrow q$ est l’énoncé ( $(\mathrm{NON}-p) \mathrm{OU} q$ ). Cet énoncé est faux dans le seul cas où $p$ est vrai et $q$ est faux. Les valeurs logiques prises par l’implication de $q$ par $p$ sont résumées dans la table de vérité

La négation de $p \longrightarrow q$ est l’énoncé ( $p \mathrm{ET}$ ( NON $-q$ )).

Lorsque $p \longrightarrow q$ est un énoncé vrai, on note $p \Longrightarrow q$ et on dit :

«si $p$ alors $q$ » ou « $p$ entraîne $q$ » ou « $p$ implique $q$ » ou « $q$ est une condition nécessaire de $p$ » ou $\ll p$ est une condition suffisante de $q>$ ou «il suffit d’avoir $p$ pour avoir $q$ » ou «il faut avoir $q$ pour avoir $p$. »

Exemples. (1) Soit $f$ une fonction définie sur $\mathbb{R}$. Si $p$ est l’énoncé : « la fonction $f$ est dérivable sur $\mathbb{R}$ » et $q$ est « la fonction $f$ est continue sur $\mathbb{R}>$, l’implication de $q$ par $p$ est vraie donc $p \Longrightarrow q$. (2) Si $p$ est l’énoncé : « $N=13423467718147$ est un nombre premier» et $q$ est « 2 est un nombre pair $\gg$, l’implication de $q$ par $p$ est vraie donc on peut écrire $p \Longrightarrow q$. (3) Si $p$ est l’énoncé : «la somme des angles d’un triangle est de 400 degrés» et $q$ est « tous les triangles sont isocèles », l’implication de $q$ par $p$ est aussi vraie donc $p \Longrightarrow q$.

Remarque. (1) D’après la table de vérité de $p \longrightarrow q$, on voit que l’implication $p \longrightarrow q$ est vraie lorsque $q$ est vraie mais sans que $p$ soit vraie. On voit aussi que l’implication $p \longrightarrow q$ est vraie lorsque $p$ est fausse, peu importe que l’assertion $q$ soit vraie ou fausse.

L’implication mathématique $p \rightarrow q$ peut donc être vraie sans qu’il y ait un quelconque rapport de cause à effet entre $p$ et $q$. (2) Affirmer « si $p$ alors $q$ » ne signifie pas que $p$ ou $q$ soit vraie. Il s’agit d’une formule reliant logiquement deux assertions $p$ et $q$ sans que les valeurs logiques de l’une ou l’autre soient déterminées.

Prenons, par exemple, pour $p$ l’assertion «il fait jour» et pour q l’assertion «il fait clair. » — Lorsque l’on dit «s’il fait jour alors il fait clair», on souligne seulement le rapport d’implication entre $p$ et $q$. — Lorsque l’on dit «puisqu’il fait jour, il fait clair», on signifie par là non seulement le rapport d’implication entre les deux assertions mais on indique également que $p$ est vraie, ce qui correspond à l’enchainement « $p$ est vraie et ( $p \longrightarrow q$ ) est vraie, donc $q$ est vraie» qui permet de déduire $q$ à partir de $p$.

Il faut donc distinguer «implication» et « déduction. »

On prendra garde à ne pas considérer ⟹ comme un raccourci pour «donc. » Il n’en a pas le sens !

Exercice 3. Soient $p, q, r$ trois assertions. Former la table de vérité de

Equivalence. Etant donnés deux énoncés mathématiques $p, q$, l’équivalence de $p$ et $q$ noté $p \longleftrightarrow q$ est l’énoncé ( $p \longrightarrow q$ ) ET ( $q \longrightarrow p$ ). Cet énoncé est vrai dans les deux seuls cas où $p$ et $q$ sont simultanément vrais ou simultanément faux. Les valeurs logiques prises par l’équivalence de $p$ et $q$ sont résumées dans la table de vérité

Si $p \Longrightarrow q$ est un théorème (ie. $p \longrightarrow q$ est vrai), alors $q \Longrightarrow p$ est l’implication réciproque (qui n’est pas toujours vrai). Si le théorème et sa réciproque sont vrais, on dit que les énoncés $p$ et $q$ sont équivalents et on note $p \Longleftrightarrow q$. On dit alors

« $p$ équivaut à $q$ » ou " $p$ si et seulement si $q$ » ou « il faut et il suffit d’avoir $p$ pour avoir $q$ » ou « $p$ est une condition nécessaire et suffisante de $q$ ».

Principe de contrapositon. Pour prouver un énoncé de type «si $p$ alors $q$ », il faut et il suffit de prouver l’énoncé «si ( NON - q) alors ( NON - p). L’énoncé $((\mathrm{NON}-q) \longrightarrow(\mathrm{NON}-q))$ s’ appelle implication contraposée de $p \longrightarrow q$. On a donc l’équivalence

Remarque. La phrase « $p$ seulement si $q$ » est à comprendre dans le sens «si NON- $q$ alors NON - $p$ » qui est donc une formulation équivalente de «si $p$ alors $q$. »

Exemple. Pour tout $n \in \mathbb{N}$, si $n^{2}$ est pair alors $n$ est pair.

8.2 Définition d’un ensemble. Relation d’appartenance. Inclusion.¶

Un ensemble peut être défini de deux manières : soit en précisant ses éléments, soit en indiquant une propriété commune vérifiée par ses éléments.

Par exemple, l’ensemble $\mathbb{U}_{3}$ des racines cubiques de l’unité peut être défini par :

où $j$ désigne le nombre $\mathrm{e}^{\frac{2 i \pi}{3}}$.

8.2.1 Définition d’un ensemble par extension.¶

Un ensemble est entièrement déterminé par ses éléments. On peut alors noter les éléments séparés par une virgule et on «enferme» le tout entre deux accolades.

Exemples. (1) L’ensemble des lettres de l’alphabet : $L=\{a, b, c, d, e, f, \ldots, x, y, z\}$. (2) Si $n$ est un entier naturel non nul, l’ensemble des restes «modulo $n »: R(n)= \{0,1,2, \ldots, n-1\}$,

(3) L’ensemble des entiers pairs est $2 \mathbb{Z}=\{2 k \mid k \in \mathbb{Z}\}$. (4) L’ensemble des rationnels est $\mathbb{Q}=\left\{\left.\frac{p}{q} \right\rvert\, p \in \mathbb{Z}, q \in \mathbb{N}^{*}\right\}$.

Remarques. (1) L’ordre dans lequel on écrit les éléments d’un ensemble entre les accolades n’a pas d’importance. (2) La répétition d’un élément dans la notation d’un ensemble n’augmente pas l’ensemble en question : par exemple, $\{a, a, a, b, b, c\}=\{a, b, c\}$.

Définition. Un ensemble admettant un seul élément est appelé un singleton. Un ensemble admettant exactement deux éléments s’appelle une paire.

Remarque. Soit $a$ un élément d’un ensemble. Il ne faut pas confondre l’élément $a$ et le singleton $\{a\}$.

8.2.2 Définition d’un ensemble par sélection (ou compréhension).¶

Soit $\mathscr{P}$ une formule mathématique quelconque définie sur un univers $\mathcal{U}$, pouvant être valable ou non pour tous les éléments de $\mathcal{U}$. On appelle $x$ l’élément générique ou la variable parcourant l’univers $\mathcal{U}$ et on notera $\mathscr{P}(x)$ la formule obtenue pour l’élément $x$. On dit que $\mathscr{P}(x)$ est un prédicat à une variable. Par exemple, (1) $\mathscr{P}(x):<x \leq \sqrt{x}+\frac{1}{\sqrt{x}} \gg$ définit un prédicat défini sur $\left.\mathcal{U}=\right] 0,+\infty[$, (2) $\mathscr{P}(x):<-x^{2}+1$ est un multiple entier de $4 \gg$ définit un prédicat défini sur $\mathcal{U}=\mathbb{Z}$, (3) $\mathscr{P}(x):$ « $x$ est dérivable sur l’intervalle $I$ » est un prédicat défini sur l’ensemble $\mathcal{U}$ des fonctions de $I$ dans $\mathbb{R}$, noté $\mathscr{F}(I, \mathbb{R})$.

Un ensemble ${ }^{1}$ peut alors être défini par les éléments de $\mathcal{U}$ partageant une même propriété $\mathscr{P}$. Si on appelle $A$ cet ensemble, on notera

( $A$ est l’ensemble des éléments $x$ appartenant à $\mathcal{U}$ tels que $\mathscr{P}(x)$ est une assertion vraie.) Exemples. (1) L’ensemble des entiers pairs est $2 \mathbb{Z}=\{m \in \mathbb{Z} \mid \exists k \in \mathbb{Z}, m=2 k\}$. (1) $2 \pi \mathbb{Z}=\left\{x \in \mathbb{R} \mid \mathrm{e}^{i x}=1\right\}$.

Dans la suite $E$ est un ensemble, par exemple $\mathbb{N}, \mathbb{Z}, \mathbb{Q}, \mathbb{R}$ ou $\mathbb{C}$.

8.2.3 Relation d’appartenance¶

• Dire que $x$ est un élément de $E$ se note $x \in E$.

• Dans le cas contraire, dire que $x$ n’est pas élément de $E$ se note $x \notin E$.

Exemple. Soit $\mathcal{D}(\mathbb{R}, \mathbb{R})$ l’ensemble des fonctions dérivables sur $\mathbb{R}$. Vous savez que exp, $\sin$, cos sont dérivables sur $\mathbb{R}$. On écrira donc

En revanche, la fonction abs : $x \in \mathbb{R} \mapsto|x|$ n’est pas dérivable en 0 . On écrira donc abs $\notin \mathcal{D}(\mathbb{R}, \mathbb{R})$.

8.2.4 Inclusion¶

• On dit que $A$ est une partie de $E$ ou un sous-ensemble de $E$ si tous les éléments de $A$ sont des éléments de $E$. On dit que $A$ est inclus dans $E$ et cette relation se note $A \subset E$.

Exemples. (1) $\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C}$. (2) On note $C(\mathbb{R}, \mathbb{R})$ l’ensemble des fonctions continues sur $\mathbb{R}$ à valeurs réelles. Toute fonction dérivable sur $\mathbb{R}$ étant continue sur $\mathbb{R}$, on peut écrire $\mathcal{D}(\mathbb{R}, \mathbb{R}) \subset C(\mathbb{R}, \mathbb{R})$.

Egalité de deux ensembles. Soient $A, B$ deux ensembles. On a l’équivalence suivante :

Pour montrer l’égalité entre deux ensembles, on montrera que l’un est inclus dans l’autre et que l’inclusion réciproque est vraie aussi.

Remarque. Il ne faut pas confondre les symboles $\in$ et $\subset$ : si $A=\{1, \sqrt{2}, \sqrt{3}, \sqrt{6}\}$, on note $\sqrt{2} \in A$ mais $\{\sqrt{2}\} \subset A$.

Définition. Il existe un ensemble unique noté $\varnothing$ et appelé ensemble vide. Cet ensemble vide est inclus dans tout ensemble $X$.

Remarque. On note aussi $\varnothing=\{ \}$.

Exercice 4. Soit $n \in \mathbb{N}^{*}$ tel que $n \geq 2$. Former un ensemble $X$ possédant $n$ éléments tel que de deux éléments pris quelconque dans $X$, l’un est élément de l’autre.

Exercice 5. Former un ensemble non vide $X$ tel que chacun des éléments de $X$ sont aussi des sous-ensembles de $X$.

8.3 Quantificateurs¶

Le langage mathématique se distingue du langage courant par l’emploi de variables. Dans une assertion mathématique, il peut intervenir des ensembles ( $\mathbb{N}, \mathbb{R}, \mathbb{C}, \ldots$ ), des constantes $(0, \pi, \mathrm{e}, \sqrt{2}, \ldots)$, des variables $(x, y, z, t, \ldots)$, des opérations $(+, \times, \cap, \cup, \ldots)$, des relations $(=, \leq,<, \ldots)$, des symboles $(\forall, \exists, \Longrightarrow, \Longleftrightarrow, \ldots)$. Mais des phrases telles que « $x^{2}=-1$ » ou « $f(x)-f(y)$ est positif» ne sont pas des assertions car elles sont incomplètes : on ne peut dire si elles sont vraies ou fausses. Que leur manque-t-il ? Les deux énoncés ci-dessus comportent des variables qui doivent être quantifiées. Dans la suite $E$ désigne un ensemble et $A$ une partie de $E$ définie par une propriété $\mathscr{P}$ :

8.3.1 Quantificateur existentiel¶

Dire que l’ensemble $A$ est non vide signifie qu’il contient au moins un élément vérifiant la propriété $\mathscr{P}$. On dit alors : « il existe $x \in E$ vérifiant $\mathscr{P}(x) »$ et on note

Exemple. Considérons le prédicat $\mathscr{P}(x)$ : « $x$ est un entier naturel pair et premier » et l’ensemble $A=\{x \in \mathbb{N} \mid \mathscr{P}(x)\}$.

Comme $A$ est non vide, (en effet $2 \in A$ ), on peut écrire :

8.3.2 Quantificateur universel¶

Dire que l’ensemble $A$ est l’ensemble $E$ tout entier signifie que tous les éléments de $E$ vérifient la propriété $\mathscr{P}$.

Exemple. Considérons le prédicat $\mathscr{P}(x)$ : « $x^{2} \geq 0$ » et l’ensemble $A=\{x \in \mathbb{R} \mid \mathscr{P}(x)\}$. Comme $A$ est l’ensemble $\mathbb{R}$ tout entier, on peut écrire :

Remarque. Les formules $(\forall x \in E)(\mathscr{P}(x))$ et $(\exists x \in E)(\mathscr{P}(x))$ sont des assertions qui peuvent être vraies ou fausses, indépendamment de la valeur attribuée à $x$. On pourrait remplacer $x$ par n’importe quelle autre lettre $y, z, t, \ldots$ sans changer le sens de l’assertion. On dit que les assertions « $(\forall x \in E)(\mathscr{P}(x)) »$ et « $(\exists x \in E)(\mathscr{P}(x)) »$ ne dépendent pas de la variable $x$ ou encore que la variable $x$ est muette dans ces formules.

Les symboles $\forall, \exists$ ne sont pas des abréviations pour les expressions « quel que soit, il existe» mais des symboles soumis à des règles d’emploi strictes.

8.3.3 Manipulation des quantificateurs¶

Règle 1. Permuter deux quantificateurs de même nature ne change pas le sens de la phrase.

Ainsi, écrire $\ll(\exists x \in E)(\exists y \in E)(\mathscr{P}(x, y))>$ revient au même que $<(\exists y \in E)(\exists x \in E)(\mathscr{P}(x, y))$. » De même, écrire $\ll(\forall x \in E)(\forall y \in E)(\mathscr{P}(x, y))>$ revient au même que $<(\forall y \in E)(\forall x \in E)(\mathscr{P}(x, y))$. »

Permuter deux quantificateurs différents change en général le sens de la phrase.

Exemple. L’assertion : $<(\forall x \in \mathbb{R})(\exists y \in \mathbb{R})(y<x)>$ est vraie puisque un réel étant fixé, on peut toujours trouver un plus petit que ce réel. Par contre l’assertion : $<(\exists y \in \mathbb{R})(\forall x \in \mathbb{R})(y<x)>$ est fausse puisque elle signifie qu’il existe un réel qui est strictement plus petit que n’importe quel nombre réel.

Exemple. L’assertion : $\left\langle(\forall x \in \mathbb{R})(\exists y \in \mathbb{R})\left(x=y^{3}\right)\right\rangle$ est vraie puisque tout nombre réel admet une racine cubique. Par contre l’assertion : « $(\exists y \in \mathbb{R})(\forall x \in \mathbb{R})\left(x=y^{3}\right) »$ signifie qu’il existe un réel dont le cube est égal à n’importe quel nombre réel, et impliquerait que $\mathbb{R}$ ne contient qu’un seul élément, ce qui est faux.

Règle 2. $<(\forall x \in E)(\mathscr{P}(x)$ et $\mathscr{Q}(x))>$ revient à $<((\forall x \in E)(\mathscr{P}(x)))$ et $((\forall x \in E)(\mathscr{Q}(x)))>$

Règle 3. « $(\exists x \in E)(\mathscr{P}(x)$ ou $\mathscr{Q}(x)) »$ revient à $<((\exists x \in E)(\mathscr{P}(x)))$ ou $((\exists x \in E)(\mathscr{Q}(x)))>$

L’assertion $<(\exists x \in E)(\mathscr{P}(x)$ et $\mathscr{Q}(x))>$ implique $<((\exists x \in E)(\mathscr{P}(x)))$ et $((\exists x \in E)(\mathscr{Q}(x))) »$ mais la réciproque est fausse comme le montre l’exemple suivant.

Exemple. On considère les prédicats suivants $-\mathscr{P}(x):<x$ est un entier naturel pair»; $-\mathscr{Q}(x):<x$ est un entier naturel impair. » L’assertion $<((\exists x \in \mathbb{N})(\mathscr{P}(x)))$ et $((\exists x \in \mathbb{N})(\mathscr{Q}(x)))>$ est vraie mais l’assertion $\ll(\exists x \in \mathbb{N})(\mathscr{P}(x)$ et $\mathscr{Q}(x))$ » est fausse puisque un entier ne peut être à la fois pair et impair.

L’assertion $<((\forall x \in E)(\mathscr{P}(x)))$ ou $((\forall x \in E)(\mathscr{Q}(x)))>$ implique $<(\forall x \in E)(\mathscr{P}(x)$ ou $\mathscr{Q}(x)) »$ mais la réciproque est fausse comme le montre l’exemple suivant.

Exemple. On considère les propriétés suivantes $-\mathscr{P}(x):<x$ est un entier naturel pair»; $-\mathscr{Q}(x):$ « $x$ est un entier naturel impair».

L’assertion $\ll(\forall x \in \mathbb{N})(\mathscr{P}(x)$ ou $\mathscr{Q}(x))>$ est vraie mais l’assertion $\ll((\forall x \in \mathbb{N})(\mathscr{P}(x)))$ ou $((\forall x \in \mathbb{N})(\mathscr{Q}(x)))$ » est fausse puisque les entiers n’ ont pas tous la même parité.

Exercice 6. Déterminer les fonctions continues $f: \mathbb{R} \rightarrow \mathbb{R}$ telles que :

Exercice 7. Traduire sous forme quantifiée, les phrases suivantes (1) «on peut trouver un entier supérieur à n’importe quel rationnel strictement positif.» (2) «tout nombre complexe admet au moins une racine carrée dans $\mathbb{C}$ » (3) «le module de la différence de deux nombres complexe est toujours supérieur ou égal à la différence des modules de ces deux nombres » (4) «La fonction $f$ s’ annule sur tout intervalle de longueur $2 \pi$.» (5) «La fonction $f$ s’annule sur $\mathbb{R}$ » (6) «La fonction $f$ est nulle sur $\mathbb{R}$ » (7) «La suite $\left(u_{n}\right)_{n \in \mathbb{N}}$ n’est pas majorée.»

Exercice 8. Traduire en langage courant la phrase suivante :

Règle 4. La négation d’une propriété contenant un certain nombre de quantificateurs $\forall$ et $\exists$ s’ obtient en remplaçant chaque quantificateur $\forall$ par le quantificateur $\exists$ et vice-versa, et la propriété $\mathscr{P}$ par la propriété (non $\mathscr{P}$ ).

Exercice 9. Soient $A, B$ deux ensembles. Quelle est la négation de $A \subset B$ sous forme quantifiée ?

Exercice 10. Soit $f: \mathbb{R} \longrightarrow \mathbb{R}$ une fonction. Dire que la fonction $f$ est croissante se traduit par

Nier cette assertion.

Exercice 11. Donner sous forme quantifiée, la négation de la phrase suivante «il existe des réels distincts ayant le même cube. »

Exercice 12. Soit $\left(u_{n}\right)_{n \in \mathbb{N}}$ une suite de réels. Dire que la suite $\left(u_{n}\right)_{n \in \mathbb{N}}$ converge vers un nombre réel $\ell$ se traduit par

Nier cette assertion.

8.4 Opérations ensemblistes : intersection, union, complémentaire.¶

8.4.1 Ensemble des parties.¶

• On appelle ensemble des parties de $E$, que l’on note $\mathscr{P}(E)$, l’ensemble formé de tous les sous-ensembles de $E$. Il contient $E$ lui même et l’ensemble vide $\varnothing$. On a donc l’équivalence suivante :

Exemples. (1) Si $E=\{0,1,2\}$ alors $\mathscr{P}(E)=\{\varnothing,\{0\},\{1\},\{2\},\{0,1\},\{0,2\},\{1,2\}, E\}$ (2) Si $E=\varnothing$ alors $\mathscr{P}(E)=\{\varnothing\}$ (3) Si $E=\{\varnothing\}$ alors $\mathscr{P}(E)=\{\varnothing,\{\varnothing\}\}$ (4) Si $E=\{\varnothing,\{\varnothing\}\}$ alors $\mathscr{P}(E)=\{\varnothing,\{\varnothing\},\{\{\varnothing\}\},\{\varnothing,\{\varnothing\}\}\}$ (5) Si $E=\{\varnothing,\{\varnothing\},\{\{\varnothing\}\}\}$ alors $\mathscr{P}(E)=\cdots$

Dans $\mathscr{P}(E)$, on définit les opérations suivantes : intersection, union, passage au complémentaire. Soient $A$ et $B$ deux sous-ensembles de $E$.

- Intersection.¶

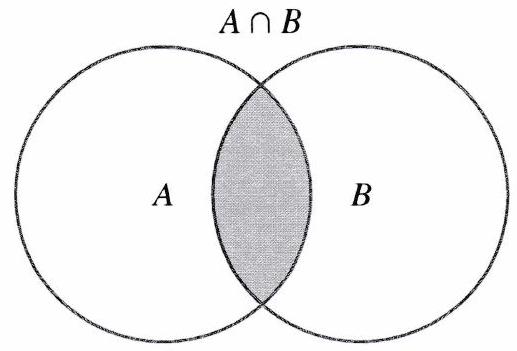
L’intersection de $A$ et $B$, notée $A \cap B$, est l’ensemble des éléments qui appartiennent à la fois à $A$ et à $B$.

On a donc l’équivalence suivante :

- Union.¶

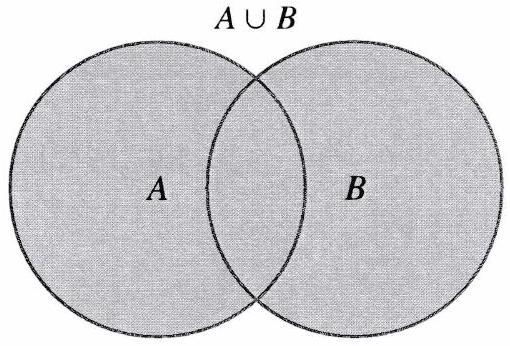
L’union de $A$ et $B$, notée $A \cup B$, est l’ensemble des éléments qui appartiennent à $A$ ou à $B$.

On a donc l’équivalence suivante :

- Passage au complémentaire.¶

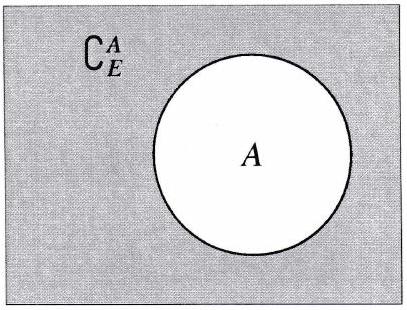
Le complémentaire de $A$ dans $E$ noté □ $C_{E}^{A}$ ou $\bar{A}$ ou $E \backslash A$ est l’ensemble des éléments de $E$ qui n’appartiennent pas à $A$.

On a donc l’équivalence suivante :

Exemples. Prenons $E=\mathbb{C}$

• si $A$ est l’ensemble des entiers naturels pairs et $B$ celui des entiers naturels impairs alors $A \cup B=\mathbb{N}$,

• si $A$ est l’ensemble des entiers naturels pairs et $B$ celui des entiers naturels multiples de 3 alors $A \cap B$ est l’ensemble des entiers naturels multiples de 6 ,

• si $A$ est l’ensemble des nombres réels plus grands que 1 et $B$ celui des nombres réels plus petits que -1 alors $A \cap B=\varnothing$

Définition. Lorsque $A \cap B=\varnothing$, on dit que $A$ et $B$ sont disjoints.

Proposition. Soient $A, B, C$ trois parties d’un ensemble $E$. (1) Si $A \subset B$ alors $A \cup B=B$ (2) Si $A \subset B$ alors $A \cap B=A$ (3) $A \cup(B \cup C)=(A \cup B) \cup C$ (4) $A \cap(B \cap C)=(A \cap B) \cap C$ (5) $A \cup B=B \cup A$ et $A \cap B=B \cap A$

Proposition. Soient $A, B, C$ trois parties de $E$. (1) $A \cap(B \cup C)=(A \cap B) \cup(A \cap C)$ (2) $A \cup(B \cap C)=(A \cup B) \cap(A \cup C)$ (3) $C_{E}^{A \cap B}=C_{E}^{A} \cup C_{E}^{B}$ (4) $C_{E}^{A \cup B}=C_{E}^{A} \cap C_{E}^{B}$

8.4.2 Produit cartésien¶

Définition. Soient $A, B$ deux ensembles. On appelle produit cartésien de $A$ et $B$, noté $A \times B$ (on prononce « $A$ croix $B$ »), l’ensemble formé des couples déléments de $A$ et $B$ pris dans cet ordre :

Remarques. (1) Soient $a, a^{\prime}$ des éléments pris dans un ensemble $A$ et et $b, b^{\prime}$ des éléments pris dans un ensemble $B$.

On a l’équivalence : $(a, b)=\left(a^{\prime}, b^{\prime}\right) \Longleftrightarrow\left(a=a^{\prime} \mathbf{E T} b=b^{\prime}\right)$. (2) Il ne faut pas confondre le couple $(a, b)$ et la paire $\{a, b\}: l$ 'ordre de notation des éléments n’a pas d’importance dans la paire $\{a, b\}=\{b, a\}$ tandis qu’il est essentiel dans le couple $(a, b)$ puisque si $a \neq b$, les couples $(a, b)$ et $(b, a)$ sont distincts. (3) Soient $A, B$ deux ensembles. On a l’équivalence :

Exemple. Avec $A=\{1,2\}$ et $B=\{3,4,5\}$, on a

En général, $A \times B$ n’est pas égal à $B \times A$.

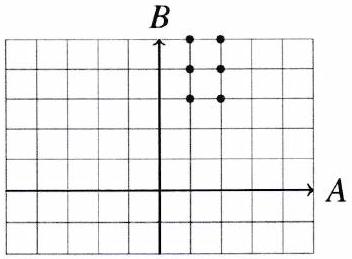
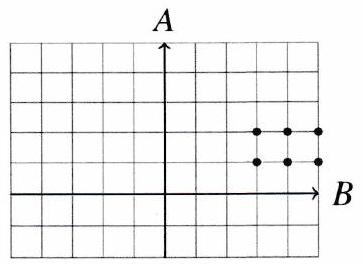
Exemple. Autre exemple, $\left(\sqrt{2}, \frac{4}{5}\right) \in \mathbb{R} \times \mathbb{Q}$ mais $\left(\frac{4}{5}, \sqrt{2}\right) \notin \mathbb{R} \times \mathbb{Q}$.

Le produit cartésien $A \times A$ est noté $A^{2}$. De façon plus générale, soit $n \in \mathbb{N}^{*}$ et $A_{1}, A_{2}, \ldots, A_{n}$ des ensembles, le produit cartésien de $A_{1}, A_{2}, \ldots, A_{n}$ noté $A_{1} \times A_{2} \times \cdots \times A_{n}$, est l’ensemble

Un élément de cet ensemble s’appelle un $n$-uplet. Le produit cartésien $\underbrace{A \times A \times \cdots \times A}_{n \text { facteurs }}$ est noté $A^{n}$. Un élément de $A^{n}$ s’ appelle une $n$-liste d’éléments de $A$.

8.5 Opérations ensemblistes et connecteurs logiques.¶

8.5.1 Négation¶

Considérons un ensemble $A$ défini par une propriété $\mathscr{P}$ :

Cet ensemble possède un complémentaire dans $E$ qui est lui même défini par une propriété qui est la négation de $\mathscr{P}: N O N-\mathscr{P}$,

Exemples. (1) Si $\mathscr{P}(x)$ est « $x$ est un entier pair» alors NON $-\mathscr{P}(x)$ est $\ll x$ est un entier impair ». (2) Si $\mathscr{P}(x)$ est « $x$ est un réel solution de $x^{2}-1<2 x>$ alors NON $-\mathscr{P}(x)$ est « $x$ est un réel solution de $x^{2}-1 \geq 2 x \gg$.

8.5.2 Conjonction¶

Considérons deux ensembles $A$ et $B$ définis respectivement par les propriétés $\mathcal{P}, Q$ :

L’ ensemble $A \cap B$ est lui même défini par une propriété qui est la conjonction de $\mathscr{P}$ et $\mathscr{Q}: \mathscr{P}$ ET $\mathscr{Q}$,

Exemples. (1) Si $\mathscr{P}(x)$ est « $x$ est un entier pair» et $\mathscr{Q}(x)$ est « $x$ est un entier multiple de $3 \gg$ alors $\mathscr{P}(x)$ et $\mathscr{Q}(x)$ est « $x$ est un entier multiple de $6>$. (2) Si $\mathscr{P}(x)$ est $\ll x$ est un réel solution de $x^{2}-1<2>\mathscr{Q}(x)$ est « $x$ est un réel solution de $x^{2}+1>2 \gg$ alors $\mathscr{P}(x)$ et $\mathscr{Q}(x)$ est $<x$ est un réel solution de $1<x^{2}<3$.»

8.5.3 Disjonction¶

Considérons deux ensembles $A$ et $B$ définis respectivement par les propriétés $\mathscr{P}, \mathscr{Q}$ :

L’ ensemble $A \cup B$ est lui même défini par une propriété qui est la disjonction de $\mathscr{P}$ et $\mathscr{Q}: \mathscr{P}$ OU $\mathscr{Q}$,

Exemples. (1) Si $\mathscr{P}(x)$ est « $x$ est un entier pair» et $\mathscr{Q}(x)$ est « $x$ est un entier impair» alors $\mathscr{P}(x)$ ou $\mathscr{Q}(x)$ est « $x$ est un entier. »

16 Rudiments de logique et vocabulaire ensembliste. (2) Si $\mathscr{P}(x)$ est « $x$ est un réel vérifiant $x \leq 0$ » $\mathscr{Q}(x)$ est « $x$ est un réel vérifiant $x>0$ » alors $\mathscr{P}(x)$ OU $\mathscr{Q}(x)$ est « $x$ est un réel positif ou nul. »

8.6 Modes de raisonnement¶

On fera attention, dans les raisonnements, à ne pas commettre les erreurs suivantes : (1) commencer une preuve en supposant la conclusion (2) confondre condition nécessaire et condition suffisante (3) donner un (ou des) exemple(s) particulier(s) ne prouve pas un cas général (mais l’expérimentation est utile) ; (4) faire usage de l’équivalence quand elle n’est pas vraie

8.6.1 Raisonnement direct¶

Montrer $P$ ou $Q$.¶

On peut établir que l’une des deux assertions est vraie ou encore montrer « si NON $P$ alors $Q$. »

Exercice 13. Soient $n, p$ des entiers naturels. Montrer que $n p$ est pair ou $n^{2}-p^{2}$ est multiple de 8.

Montrer si P alors Q.¶

Le raisonnement doit commencer par «Supposons $P$. » et se terminer par «... donc $Q$.»

Montrer P ssi Q.¶

Il s’agit de démontrer ici une équivalence. Il est possible d’établir une équivalence en raisonnant par équivalence, c’est à dire par un enchainement de propriétés toutes équivalentes à $P$ jusqu’à obtenir $Q$ mais ces situations sont assez rares en pratique.

Le raisonnement s’effectue en général en deux étapes : — dans un premier temps, on prouve «si $P$ alors $Q$ » (c’-à-d. $Q$ est une condition nécessaire de $P$ ), et

• dans un second temps, on prouve «si $Q$ alors $P$ » ( $Q$ est une condition suffisante de P.)

On peut commencer par l’une ou par l’autre de ces deux implications mais il arrive souvent que l’une des deux est plus aisée à établir que l’autre.

Exercice 14. Pour tout $n \in \mathbb{N}^{*}$, on note $\mathbb{U}_{n}$ l’ensemble des racines $n$-èmes de l’unité.

Soient $p, q$ deux entiers naturels non nuls. Montrer que $\mathbb{U}_{p} \subset \mathbb{U}_{q}$ si et seulement si $q$ est multiple de $p$.

Exercice 15. Soit $n \in \mathbb{N}^{*}$. Montrer que le polynôme $X^{n}+X+1$ admet une racine dans U si et seulement si $n$ est de la forme $n=3 m+2$ où $m \in \mathbb{N}$.

Montrer pour tout $x \in E, \mathscr{P}(x)$.

La démonstration doit commencer par « Soit $x \in E »$ puis il faut établir $\mathscr{P}(x)$. Lorsque $E=\mathbb{N}$, on peut aussi envisager le raisonnement par récurrence, développé plus loin.

Montrer pour tout $x \in E, \mathbf{s i} \mathscr{P}(x)$ alors $\mathscr{Q}(x)$.

La démonstration doit commencer par « Soit $x \in E$ tel que $\mathscr{P}(x) »$ ou « Soit $x \in E$ et supposons $\mathscr{P}(x)$. » puis il faut établir $\mathscr{Q}(x)$.