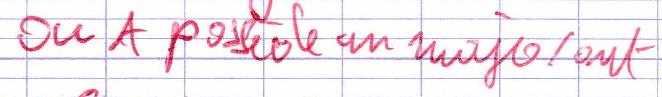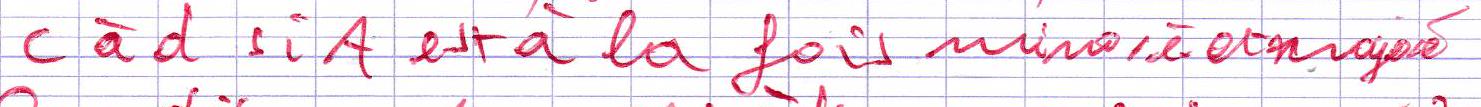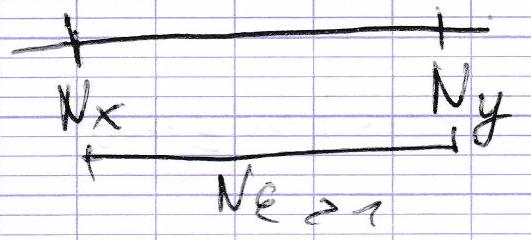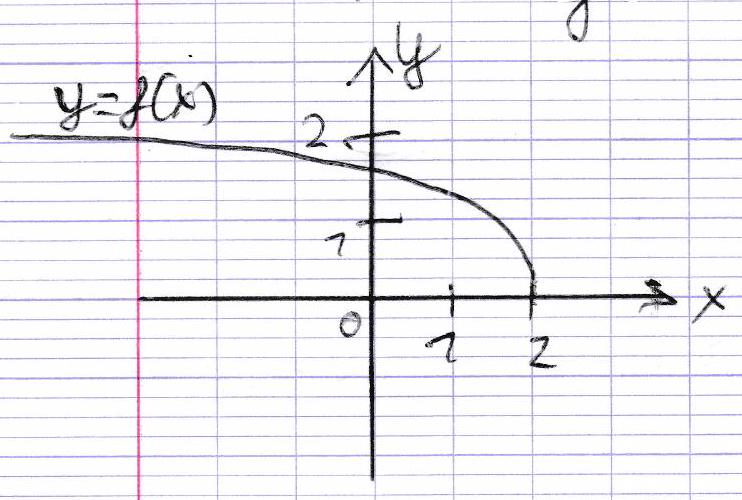Chapitre 210 : Nombres réels et suites numériques Quelques rappels : majorant/minorant
On dit que A A A
M ∈ R M \in \mathbb{R} M ∈ R ∀ x ∈ A , x ≤ M \forall x \in A, x \leq M ∀ x ∈ A , x ≤ M
Un tel M M M A A A A A A ( ∃ M ∈ R ) ( ∀ x ∈ A ) ( x ≤ M ) (\exists M \in \mathbb{R})(\forall x \in A)(x \leq M) ( ∃ M ∈ R ) ( ∀ x ∈ A ) ( x ≤ M )
On dit que A A A ( ∃ m ∈ R ) ( ∀ x ∈ A ) ( m ≤ x ) (\exists m \in \mathbb{R})(\forall x \in A)(m \leq x) ( ∃ m ∈ R ) ( ∀ x ∈ A ) ( m ≤ x )
On dit que A A A ( ∃ m ∈ R ) ( ∃ M ∈ R ) ( ∀ x ∈ A ) ( m ≤ x ≤ M ) (\exists m \in \mathbb{R})(\exists M \in \mathbb{R})(\forall x \in A)(m \leq x \leq M) ( ∃ m ∈ R ) ( ∃ M ∈ R ) ( ∀ x ∈ A ) ( m ≤ x ≤ M )
A admet un maximum ssi A A A A A A
α = max ( A ) \alpha = \max (A) α = max ( A )
c’est-à-dire si A A A
Dans ce cas, le réel μ \mu μ A A A min ( A ) \min (A) min ( A )
Exemples : ¶ N \mathbb{N} N N \mathbb{N} N
[ 0 , 1 [ [0,1[ [ 0 , 1 [ [ 0 , 1 [ [0,1[ [ 0 , 1 [ x ∈ [ 0 , 1 [ x \in [0,1[ x ∈ [ 0 , 1 [ 0 ≤ x < 1 0 \leq x < 1 0 ≤ x < 1 x < 1 x < 1 x < 1 y ∈ [ 0 , 1 [ y \in [0,1[ y ∈ [ 0 , 1 [ x < y < 1 x < y < 1 x < y < 1
A = { 1 + 1 n ∣ n ∈ N ∗ } A = \left\{1 + \frac{1}{n} \mid n \in \mathbb{N}^*\right\} A = { 1 + n 1 ∣ n ∈ N ∗ }
A A A n ∈ N ∗ n \in \mathbb{N}^* n ∈ N ∗ 1 < 1 + 1 n + 1 < 1 + 1 n 1 < 1 + \frac{1}{n+1} < 1 + \frac{1}{n} 1 < 1 + n + 1 1 < 1 + n 1 A A A
b) A = { x + 1 x ∣ x ∈ R ∗ } A = \left\{x + \frac{1}{x} \mid x \in \mathbb{R}^*\right\} A = { x + x 1 ∣ x ∈ R ∗ }
A A A
Pour tout a > 0 a > 0 a > 0 a < a + 1 a a < a + \frac{1}{a} a < a + a 1 A A A
2 = 1 + 1 1 ∈ A 2 = 1 + \frac{1}{1} \in A 2 = 1 + 1 1 ∈ A x + 1 x − 2 = x 2 − 2 x + 1 x = ( x − 1 ) 2 x ≥ 0 x + \frac{1}{x} - 2 = \frac{x^2 - 2x + 1}{x} = \frac{(x-1)^2}{x} \geq 0 x + x 1 − 2 = x x 2 − 2 x + 1 = x ( x − 1 ) 2 ≥ 0
Donc ∀ x > 0 \forall x > 0 ∀ x > 0 x + 1 x ≥ 2 x + \frac{1}{x} \geq 2 x + x 1 ≥ 2 A A A min ( A ) = 2 \min (A) = 2 min ( A ) = 2
c) Soit x ∈ R x \in \mathbb{R} x ∈ R
Posons x = tan ( t 2 ) x = \tan \left(\frac{t}{2}\right) x = tan ( 2 t ) t ∈ ] − π , π [ t \in ]-\pi, \pi[ t ∈ ] − π , π [
2 x 1 + x 2 = sin ( t ) \frac{2x}{1+x^2} = \sin(t) 1 + x 2 2 x = sin ( t ) Lorsque t t t ] − π , π [ ]-\pi, \pi[ ] − π , π [ sin ( t ) \sin(t) sin ( t ) [ − 1 , 1 ] [-1,1] [ − 1 , 1 ] 2 x 1 + x 2 \frac{2x}{1+x^2} 1 + x 2 2 x [ − 1 , 1 ] [-1,1] [ − 1 , 1 ] A A A
− 1 = 2 × ( − 1 ) 1 + ( − 1 ) 2 ∈ A , 1 = 2 × 1 1 + 1 2 ∈ A -1 = \frac{2 \times (-1)}{1 + (-1)^2} \in A, \quad 1 = \frac{2 \times 1}{1 + 1^2} \in A − 1 = 1 + ( − 1 ) 2 2 × ( − 1 ) ∈ A , 1 = 1 + 1 2 2 × 1 ∈ A Donc min ( A ) = − 1 , max ( A ) = 1 \min (A) = -1, \max (A) = 1 min ( A ) = − 1 , max ( A ) = 1
Valeur absolue ¶ Soit x ∈ R , y ∈ R x \in \mathbb{R}, y \in \mathbb{R} x ∈ R , y ∈ R
∣ x ∣ = max ( − x , x ) |x| = \max (-x, x) ∣ x ∣ = max ( − x , x )
∣ x + y ∣ ≤ ∣ x ∣ + ∣ y ∣ |x+y| \leq |x| + |y| ∣ x + y ∣ ≤ ∣ x ∣ + ∣ y ∣
∣ ∣ x ∣ − ∣ y ∣ ∣ ≤ ∣ x − y ∣ ||x| - |y|| \leq |x - y| ∣∣ x ∣ − ∣ y ∣∣ ≤ ∣ x − y ∣
Si ( x i ) i ∈ I (x_i)_{i \in I} ( x i ) i ∈ I
Alors ∣ ∑ i ∈ I x i ∣ ≤ ∑ i ∈ I ∣ x i ∣ \left|\sum_{i \in I} x_i\right| \leq \sum_{i \in I} |x_i| ∣ ∣ ∑ i ∈ I x i ∣ ∣ ≤ ∑ i ∈ I ∣ x i ∣
Bornes supérieure, borne inférieure
Soit E E E E E E E E E E E E sup ( E ) \sup (E) sup ( E )
Exemples :
E = [ a , b ] E = [a, b] E = [ a , b ]
∀ x ∈ E , x ≤ b \forall x \in E, \quad x \leq b ∀ x ∈ E , x ≤ b b b b E E E
Soit M M M E E E
Alors : ∀ x ∈ E , x ≤ M \forall x \in E, x \leq M ∀ x ∈ E , x ≤ M b ∈ E b \in E b ∈ E b ≤ M b \leq M b ≤ M
Donc b b b E E E b = sup ( E ) b = \sup (E) b = sup ( E )
E = [ a , b [ E = [a, b[ E = [ a , b [
Alors a ≤ M < b a \leq M < b a ≤ M < b
Posons x = b + M 2 x = \frac{b + M}{2} x = 2 b + M
On a : a ≤ M < x < b a \leq M < x < b a ≤ M < x < b
Donc x ∈ E x \in E x ∈ E x > M x > M x > M M M M M ≥ b M \geq b M ≥ b
Donc b = sup ( E ) b = \sup (E) b = sup ( E )
Ici, b ∉ E b \notin E b ∈ / E E E E
β \beta β E E E
tout autre majorant M M M E E E M ≥ β M \geq \beta M ≥ β
Caractérisation de la borne supérieure
Soit E E E
Soit β ∈ R \beta \in \mathbb{R} β ∈ R
β = sup ( E ) ssi { ∀ x ∈ E , x ≤ β ( ∀ ε > 0 ) ( ∃ t ∈ E ) ( β − ε < t ) (Condition) \beta = \sup (E) \text{ ssi } \left\{
\begin{array}{l}
\forall x \in E, x \leq \beta \\
(\forall \varepsilon > 0)(\exists t \in E)(\beta - \varepsilon < t)
\end{array}
\right.
\quad \text{(Condition)} β = sup ( E ) ssi { ∀ x ∈ E , x ≤ β ( ∀ ε > 0 ) ( ∃ t ∈ E ) ( β − ε < t ) (Condition) Preuve :
(CN). Supposons que β = sup ( E ) \beta = \sup (E) β = sup ( E )
Il est clair que : ∀ x ∈ E , x ≤ β \forall x \in E, x \leq \beta ∀ x ∈ E , x ≤ β β \beta β E E E
Soit ε > 0 \varepsilon > 0 ε > 0
β − ε < β \beta - \varepsilon < \beta β − ε < β
Or β \beta β E E E β − ε \beta - \varepsilon β − ε E E E t ∈ E t \in E t ∈ E t > β − ε t > \beta - \varepsilon t > β − ε
(CS) Supposons que :
{ ∀ x ∈ E , x ≤ β ( ∀ ε > 0 ) ( ∃ t ∈ E ) ( β − ε < t ) \left\{
\begin{array}{l}
\forall x \in E, x \leq \beta \\
(\forall \varepsilon > 0)(\exists t \in E)(\beta - \varepsilon < t)
\end{array}
\right. { ∀ x ∈ E , x ≤ β ( ∀ ε > 0 ) ( ∃ t ∈ E ) ( β − ε < t ) La première assertion ∀ x ∈ E , x ≤ β \forall x \in E, x \leq \beta ∀ x ∈ E , x ≤ β β \beta β E E E
Supposons par l’absurde que E E E β ′ < β \beta' < \beta β ′ < β
Alors β ′ = β − ε \beta' = \beta - \varepsilon β ′ = β − ε ε = β − β ′ \varepsilon = \beta - \beta' ε = β − β ′
D’après la deuxième assertion, il existe t ∈ E t \in E t ∈ E β − ε < t \beta - \varepsilon < t β − ε < t β ′ < t \beta' < t β ′ < t β ′ \beta' β ′ E E E
Ainsi, tout autre majorant β ′ \beta' β ′ E E E β ′ ≥ β \beta' \geq \beta β ′ ≥ β β \beta β E E E
Corollaire :
Soit E E E E E E E E E inf ( E ) \inf (E) inf ( E )
α \alpha α E E E
tout autre minorant m m m E E E m ≤ α m \leq \alpha m ≤ α
Caractérisation de la borne inférieure
Soit E E E α ∈ R \alpha \in \mathbb{R} α ∈ R
α = inf ( E ) ssi { ∀ x ∈ E , x ≥ α ( ∀ ε > 0 ) ( ∃ t ∈ E ) ( α + ε > t ) \alpha = \inf (E) \text{ ssi } \left\{
\begin{array}{l}
\forall x \in E, x \geq \alpha \\
(\forall \varepsilon > 0)(\exists t \in E)(\alpha + \varepsilon > t)
\end{array}
\right. α = inf ( E ) ssi { ∀ x ∈ E , x ≥ α ( ∀ ε > 0 ) ( ∃ t ∈ E ) ( α + ε > t ) Rappel sur la partie entière :
Soit x ∈ R x \in \mathbb{R} x ∈ R
Il existe un unique entier p ∈ Z p \in \mathbb{Z} p ∈ Z p ≤ x < p + 1 p \leq x < p+1 p ≤ x < p + 1
On note ⌊ x ⌋ \lfloor x \rfloor ⌊ x ⌋ p p p x x x
Densité de Q \mathbb{Q} Q R \mathbb{R} R
Soit x ∈ R , y ∈ R x \in \mathbb{R}, y \in \mathbb{R} x ∈ R , y ∈ R x < y x < y x < y
Alors il existe un rationnel r r r x < r < y x < r < y x < r < y
Preuve :
Supposons que x < y x < y x < y
Posons ε = y − x > 0 \varepsilon = y - x > 0 ε = y − x > 0 N = ⌊ 1 ε ⌋ + 1 N = \left\lfloor \frac{1}{\varepsilon} \right\rfloor + 1 N = ⌊ ε 1 ⌋ + 1
Alors N ε = N ( y − x ) > 1 N \varepsilon = N(y - x) > 1 Nε = N ( y − x ) > 1
p = ⌊ N x ⌋ + 1 ∈ Z p = \left\lfloor N x \right\rfloor + 1 \in \mathbb{Z} p = ⌊ N x ⌋ + 1 ∈ Z
N x < p ≤ N x + 1 < N y N x < p \leq N x + 1 < N y N x < p ≤ N x + 1 < N y
x < p N < y x < \frac{p}{N} < y x < N p < y p N ∈ Q \frac{p}{N} \in \mathbb{Q} N p ∈ Q
Conséquence de la densité
Pour tout n ∈ N n \in \mathbb{N} n ∈ N r ∈ R r \in \mathbb{R} r ∈ R x < r < x + 1 2 n x < r < x + \frac{1}{2^n} x < r < x + 2 n 1
Généralités sur les suites ¶ On appelle suite numérique toute application u : N → R u : \mathbb{N} \rightarrow \mathbb{R} u : N → R
On la note ( u n ) n ∈ N (u_n)_{n \in \mathbb{N}} ( u n ) n ∈ N
On définit aussi des suites définies à partir d’un certain rang.
Soit n 0 ∈ N n_0 \in \mathbb{N} n 0 ∈ N n 0 n_0 n 0 u : [ n 0 , + ∞ [ → R u : [n_0, +\infty[ \rightarrow \mathbb{R} u : [ n 0 , + ∞ [ → R
On la note ( u n ) n ≥ n 0 (u_n)_{n \geq n_0} ( u n ) n ≥ n 0 n ↦ u n n \mapsto u_n n ↦ u n
Exemples de suites :
Pour tout n ∈ N n \in \mathbb{N} n ∈ N u n = e − n 1 + n u_n = \frac{e^{-n}}{1 + n} u n = 1 + n e − n
Pour tout n ∈ N n \in \mathbb{N} n ∈ N u n u_n u n R + ∗ \mathbb{R}^{+*} R +∗
ln ( x ) + x = n \ln (x) + x = n ln ( x ) + x = n (implicite)
x x x 0 + ∞ +\infty + ∞ f f f − ∞ -\infty − ∞ + ∞ +\infty + ∞
lim x → 0 x > 0 f ( x ) = − ∞ , lim x → + ∞ f ( x ) = + ∞ \lim_{\substack{x \rightarrow 0 \\ x > 0}} f(x) = -\infty, \quad \lim_{x \rightarrow +\infty} f(x) = +\infty x → 0 x > 0 lim f ( x ) = − ∞ , x → + ∞ lim f ( x ) = + ∞ Elle réalise une bijection de ] 0 , + ∞ [ ]0, +\infty[ ] 0 , + ∞ [ R \mathbb{R} R ∀ n ∈ N \forall n \in \mathbb{N} ∀ n ∈ N u n ∈ ] 0 , + ∞ [ u_n \in ]0, +\infty[ u n ∈ ] 0 , + ∞ [ ln ( u n ) = n \ln (u_n) = n ln ( u n ) = n
Prenons u 0 ∈ I u_0 \in I u 0 ∈ I u 1 = f ( u 0 ) ∈ I u_1 = f(u_0) \in I u 1 = f ( u 0 ) ∈ I u 2 = f ( u 1 ) ∈ I u_2 = f(u_1) \in I u 2 = f ( u 1 ) ∈ I
On peut définir une suite ( u n ) n ∈ N (u_n)_{n \in \mathbb{N}} ( u n ) n ∈ N u 0 ∈ I u_0 \in I u 0 ∈ I ∀ n ∈ N \forall n \in \mathbb{N} ∀ n ∈ N u n + 1 = f ( u n ) u_{n+1} = f(u_n) u n + 1 = f ( u n )
(suite définie par récurrence)
Exemple : f : ] − ∞ , 2 ] → [ 0 , + ∞ [ f : ]-\infty, 2] \rightarrow [0, +\infty[ f : ] − ∞ , 2 ] → [ 0 , + ∞ [
x ↦ 2 − x x \mapsto \sqrt{2 - x} x ↦ 2 − x
L’intervalle [ − 2 , 2 ] [-2, 2] [ − 2 , 2 ] f f f 0 ∈ [ − 2 , 2 ] 0 \in [-2, 2] 0 ∈ [ − 2 , 2 ] ( u n ) n ∈ N (u_n)_{n \in \mathbb{N}} ( u n ) n ∈ N u n + 1 = f ( u n ) u_{n+1} = f(u_n) u n + 1 = f ( u n )
Notation : L’ensemble des suites numériques définies sur N \mathbb{N} N R N \mathbb{R}^{\mathbb{N}} R N
(L’ensemble des applications de N \mathbb{N} N R \mathbb{R} R
Opérations sur les suites
Soit ( u n ) n ∈ N (u_n)_{n \in \mathbb{N}} ( u n ) n ∈ N ( v n ) n ∈ N (v_n)_{n \in \mathbb{N}} ( v n ) n ∈ N λ ∈ R \lambda \in \mathbb{R} λ ∈ R
( u n ) n ∈ N + ( v n ) n ∈ N = ( u n + v n ) n ∈ N (u_n)_{n \in \mathbb{N}} + (v_n)_{n \in \mathbb{N}} = (u_n + v_n)_{n \in \mathbb{N}} ( u n ) n ∈ N + ( v n ) n ∈ N = ( u n + v n ) n ∈ N
( u n ) n ∈ N × ( v n ) n ∈ N = ( u n v n ) n ∈ N (u_n)_{n \in \mathbb{N}} \times (v_n)_{n \in \mathbb{N}} = (u_n v_n)_{n \in \mathbb{N}} ( u n ) n ∈ N × ( v n ) n ∈ N = ( u n v n ) n ∈ N
λ ( u n ) n ∈ N = ( λ u n ) n ∈ N \lambda (u_n)_{n \in \mathbb{N}} = (\lambda u_n)_{n \in \mathbb{N}} λ ( u n ) n ∈ N = ( λ u n ) n ∈ N
R N \mathbb{R}^{\mathbb{N}} R N + × + \times + ×
Soit ( u n ) n ∈ N (u_n)_{n \in \mathbb{N}} ( u n ) n ∈ N
(M est appelé majorant de la suite)
On dit que ( u n ) n ∈ N (u_n)_{n \in \mathbb{N}} ( u n ) n ∈ N ( ∃ m ∈ R ) ( ∀ n ∈ N ) ( u n ≥ m ) (\exists m \in \mathbb{R})(\forall n \in \mathbb{N})(u_n \geq m) ( ∃ m ∈ R ) ( ∀ n ∈ N ) ( u n ≥ m )
On dit que la suite ( u n ) (u_n) ( u n )
( ∃ m ∈ R ) ( ∃ M ∈ R ) ( ∀ n ∈ N ) ( m ≤ u n ≤ M ) (\exists m \in \mathbb{R})(\exists M \in \mathbb{R})(\forall n \in \mathbb{N})(m \leq u_n \leq M) ( ∃ m ∈ R ) ( ∃ M ∈ R ) ( ∀ n ∈ N ) ( m ≤ u n ≤ M )
Propriété :
Soit ( u n ) n ∈ N ∈ R N (u_n)_{n \in \mathbb{N}} \in \mathbb{R}^{\mathbb{N}} ( u n ) n ∈ N ∈ R N
La suite ( u n ) (u_n) ( u n )
Preuve :
Par définition, il existe m , M ∈ R m, M \in \mathbb{R} m , M ∈ R
∀ n ∈ N , m ≤ u n ≤ M \forall n \in \mathbb{N}, m \leq u_n \leq M ∀ n ∈ N , m ≤ u n ≤ M
Posons C = max ( ∣ m ∣ , ∣ M ∣ ) C = \max(|m|, |M|) C = max ( ∣ m ∣ , ∣ M ∣ )
Donc ∣ u n ∣ ≤ C |u_n| \leq C ∣ u n ∣ ≤ C ( u n ) (u_n) ( u n )
Alors il existe m , M ∈ R m, M \in \mathbb{R} m , M ∈ R
∀ n ∈ N , m ≤ u n ≤ M \forall n \in \mathbb{N}, m \leq u_n \leq M ∀ n ∈ N , m ≤ u n ≤ M
Donc ( u n ) (u_n) ( u n )
Donc la suite ( u n ) (u_n) ( u n )
Aloon ∀ n ∈ N , u n ⩽ M ⩽ ∣ M ∣ ⩽ C \forall n \in \mathbb{N}, \quad u_{n} \leqslant M \leqslant |M| \leqslant C ∀ n ∈ N , u n ⩽ M ⩽ ∣ M ∣ ⩽ C u n ≥ − n ≥ − ∣ m ∣ ≥ − c u_{n} \geq -n \geq -|m| \geq -c u n ≥ − n ≥ − ∣ m ∣ ≥ − c ∀ n ∈ N , ∣ U n ∣ ⩽ c \forall n \in \mathbb{N},\left|U_{n}\right| \leqslant c ∀ n ∈ N , ∣ U n ∣ ⩽ c
Il existe C ∈ R + C \in \mathbb{R}^{+} C ∈ R + ∀ n ∈ N , ∣ U n ∣ ≤ C \forall n \in \mathbb{N}, \quad\left|U_{n}\right| \leq C ∀ n ∈ N , ∣ U n ∣ ≤ C ∀ n ∈ N , − C ⩽ u n ⩽ C \forall n \in \mathbb{N}, \quad -C \leqslant u_{n} \leqslant C ∀ n ∈ N , − C ⩽ u n ⩽ C
Monotonie!
Soit ( u n ) n ∈ N ∈ R N \left(u_{n}\right)_{n \in \mathbb{N}} \in \mathbb{R}^{\mathbb{N}} ( u n ) n ∈ N ∈ R N
On dit que ( u n ) (u_n) ( u n ) ∀ n ∈ N , u n + 1 − u n ⩾ 0 \forall n \in \mathbb{N}, u_{n+1}-u_{n} \geqslant 0 ∀ n ∈ N , u n + 1 − u n ⩾ 0
On dit que ( u n ) n ∈ N \left(u_{n}\right)_{n \in \mathbb{N}} ( u n ) n ∈ N ∀ n ∈ N , u n + 1 − u n > 0 \forall n \in \mathbb{N}, u_{n+1}-u_{n} > 0 ∀ n ∈ N , u n + 1 − u n > 0
On dit que ( u n ) (u_n) ( u n ) ∀ n ∈ N , u n + 1 − u n ⩽ 0 \forall n \in \mathbb{N}, u_{n+1}-u_{n} \leqslant 0 ∀ n ∈ N , u n + 1 − u n ⩽ 0
On dit que ( u n ) (u_n) ( u n ) ∀ n ∈ N , u n + 1 − u n < 0 \forall n \in \mathbb{N}, u_{n+1}-u_{n} < 0 ∀ n ∈ N , u n + 1 − u n < 0
Suite constante / suite stationnaire:
La suite ( u n ) n ∈ N (u_n)_{n \in \mathbb{N}} ( u n ) n ∈ N ∀ n ∈ N , u n + 1 = u n \forall n \in \mathbb{N}, u_{n+1}=u_{n} ∀ n ∈ N , u n + 1 = u n
La suite ( u n ) (u_n) ( u n ) ∃ p ∈ N , ∃ K ∈ N , ∀ n ⩾ p , u n = u n + 1 \exists p \in \mathbb{N}, \exists K \in \mathbb{N}, \forall n \geqslant p, u_{n}=u_{n+1} ∃ p ∈ N , ∃ K ∈ N , ∀ n ⩾ p , u n = u n + 1
Suite arithmétique:
On dit que ( u n ) n ∈ N \left(u_{n}\right)_{n \in \mathbb{N}} ( u n ) n ∈ N u 0 ∈ R u_0 \in \mathbb{R} u 0 ∈ R r ∈ R r \in \mathbb{R} r ∈ R ∀ n ∈ N , u n + 1 − u n = r \forall n \in \mathbb{N}, u_{n+1}-u_{n}=r ∀ n ∈ N , u n + 1 − u n = r r r r
Propriété: ¶ Soit ( u n ) n ∈ N \left(u_{n}\right)_{n \in \mathbb{N}} ( u n ) n ∈ N r r r ∀ n ∈ N , ∀ p ∈ N \forall n \in \mathbb{N}, \forall p \in \mathbb{N} ∀ n ∈ N , ∀ p ∈ N
u n = u p + ( n − p ) r u n = u 0 + n r \begin{aligned}
& u_{n}=u_{p}+(n-p) r \\
& u_{n}=u_{0}+n r
\end{aligned} u n = u p + ( n − p ) r u n = u 0 + n r ∑ k = p q u k = u p + u q 2 × ( q − p + 1 ) \sum_{k=p}^{q} u_{k}=\frac{u_{p}+u_{q}}{2} \times (q-p+1) k = p ∑ q u k = 2 u p + u q × ( q − p + 1 ) En effet, pour tout n ⩾ p n \geqslant p n ⩾ p
u n − u p = ∑ k = p n − 1 ( u k + 1 − u k ) u_{n}-u_{p}=\sum_{k=p}^{n-1}\left(u_{k+1}-u_{k}\right) u n − u p = k = p ∑ n − 1 ( u k + 1 − u k ) et donc, soit λ = ∑ k = 1 q u k \lambda=\sum_{k=1}^{q} u_{k} λ = ∑ k = 1 q u k ∑ k = p q u k = ∑ k = p q u k \sum_{k=p}^{q} u_{k} = \sum_{k=p}^{q} u_{k} ∑ k = p q u k = ∑ k = p q u k S = ∑ k = p q u k S=\sum_{k=p}^{q} u_{k} S = ∑ k = p q u k 2 S = ∑ k = p q ( u k + u q − k + p ) 2S=\sum_{k=p}^{q}\left(u_{k}+u_{q-k+p}\right) 2 S = ∑ k = p q ( u k + u q − k + p ) u k + u q − k + p = u 0 + k r + u 0 + ( q − k + p ) r u_{k}+u_{q-k+p}=u_{0}+k r+u_{0}+(q-k+p) r u k + u q − k + p = u 0 + k r + u 0 + ( q − k + p ) r = u 0 + p r + u 0 + q r =u_{0}+p r + u_{0}+q r = u 0 + p r + u 0 + q r = u p + u q =u_{p}+u_{q} = u p + u q
u k + u q − k + p = u p + u q 2 S = ∑ k = p q ( u p + u q ) \begin{aligned}
& u_{k}+u_{q-k+p}=u_{p}+u_{q} \\
& 2S=\sum_{k=p}^{q}\left(u_{p}+u_{q}\right)
\end{aligned} u k + u q − k + p = u p + u q 2 S = k = p ∑ q ( u p + u q ) Suite géométrique:
La suite ( u n ) n ∈ N (u_n)_{n \in \mathbb{N}} ( u n ) n ∈ N q ∈ R q \in \mathbb{R} q ∈ R ∀ n ∈ N , u n + 1 = q u n \forall n \in \mathbb{N}, u_{n+1}=q u_{n} ∀ n ∈ N , u n + 1 = q u n q q q
Propriété:
Soit ( u n ) n ∈ N (u_n)_{n \in \mathbb{N}} ( u n ) n ∈ N q ∉ { 0 , 1 } q \notin \{0,1\} q ∈ / { 0 , 1 } ∀ n ∈ N , ∀ p ∈ N , u n = u p × q n − p \forall n \in \mathbb{N}, \forall p \in \mathbb{N}, u_{n}=u_{p} \times q^{n-p} ∀ n ∈ N , ∀ p ∈ N , u n = u p × q n − p
∑ k = s t u k = u s − u t q 1 − q \sum_{k=s}^{t} u_{k}=\frac{u_{s}-u_{t} q}{1-q} k = s ∑ t u k = 1 − q u s − u t q En effet, si u p ≠ 0 u_{p} \neq 0 u p = 0 u n ≠ 0 u_{n} \neq 0 u n = 0 n > p n > p n > p
u n u p = ∏ k = p n − 1 u k + 1 u k = q n − p \frac{u_{n}}{u_{p}}=\prod_{k=p}^{n-1} \frac{u_{k+1}}{u_{k}}=q^{n-p} u p u n = k = p ∏ n − 1 u k u k + 1 = q n − p En particulier, si s ⩾ 1 s \geqslant 1 s ⩾ 1
( 1 − q ) S = ∑ k = s t ( u k − u k + 1 ) = u s − u t + 1 = u s − q u t \begin{aligned}
(1-q) S & =\sum_{k=s}^{t}\left(u_{k}-u_{k+1}\right) \\
& =u_{s}-u_{t+1} \\
& =u_{s}-q u_{t}
\end{aligned} ( 1 − q ) S = k = s ∑ t ( u k − u k + 1 ) = u s − u t + 1 = u s − q u t Suite arithmético-géométrique:
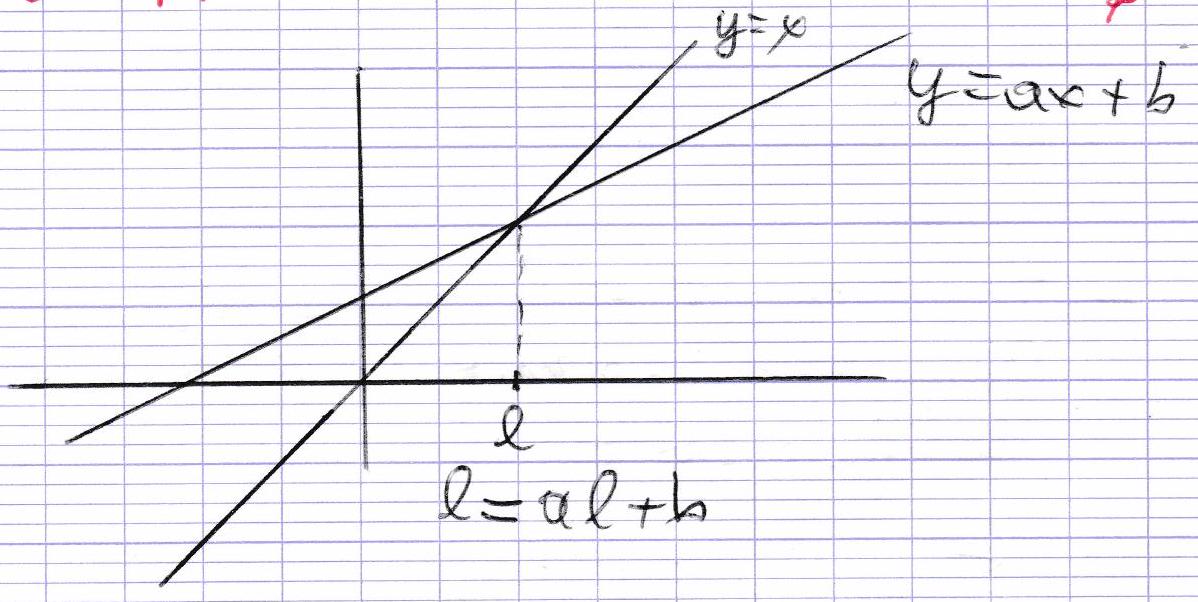
On dit que la suite ( u n ) n ∈ N \left(u_{n}\right)_{n \in \mathbb{N}} ( u n ) n ∈ N a ∈ R a \in \mathbb{R} a ∈ R b ∈ R b \in \mathbb{R} b ∈ R ∀ n ∈ N , u n + 1 = a u n + b \forall n \in \mathbb{N}, u_{n+1}=a u_{n}+b ∀ n ∈ N , u n + 1 = a u n + b
On suppose dans la suite que a ≠ 1 a \neq 1 a = 1 b ≠ 0 b \neq 0 b = 0
Pour tout n ∈ N n \in \mathbb{N} n ∈ N
u n + 1 = a u n + b l = a l + b \begin{gathered}
u_{n+1}=a u_{n}+b \\
l=a l+b
\end{gathered} u n + 1 = a u n + b l = a l + b u n + 1 − l = a ( u n − l ) u_{n+1}-l=a(u_{n}-l) u n + 1 − l = a ( u n − l ) V n = u n − l V_{n}=u_{n}-l V n = u n − l ∀ n ∈ N , V n + 1 = a V n \forall n \in \mathbb{N}, V_{n+1}=a V_{n} ∀ n ∈ N , V n + 1 = a V n
v n = v 0 a n u n − l = ( u 0 − l ) a n u n = l + ( u 0 − l ) a n \begin{aligned}
& v_{n}=v_{0} a^{n} \\
& u_{n}-l=\left(u_{0}-l\right) a^{n} \\
& u_{n}=l+\left(u_{0}-l\right) a^{n}
\end{aligned} v n = v 0 a n u n − l = ( u 0 − l ) a n u n = l + ( u 0 − l ) a n et l = b 1 − a l=\frac{b}{1-a} l = 1 − a b u n = b 1 − a + ( u 0 − b 1 − a ) a n u_{n}=\frac{b}{1-a}+\left(u_{0}-\frac{b}{1-a}\right) a^{n} u n = 1 − a b + ( u 0 − 1 − a b ) a n
Application:
{ u 0 = 2 u n + 1 = 3 u n + 2 \left\{\begin{array}{l}
u_{0}=2 \\
u_{n+1}=3 u_{n}+2
\end{array}\right. { u 0 = 2 u n + 1 = 3 u n + 2 Suite convergente:
Soit ( u n ) n ∈ N (u_n)_{n \in \mathbb{N}} ( u n ) n ∈ N l ∈ R l \in \mathbb{R} l ∈ R ( u n ) (u_n) ( u n ) l l l
( ∀ ε > 0 ) ( ∃ n 0 ∈ N ) ( ∀ n ∈ N ) ( n ⩾ n 0 ⇒ ∣ u n − l ∣ ⩽ ε ) (\forall \varepsilon > 0)\left(\exists n_{0} \in \mathbb{N}\right)(\forall n \in \mathbb{N})\left(n \geqslant n_{0} \Rightarrow \left|u_{n}-l\right| \leqslant \varepsilon\right) ( ∀ ε > 0 ) ( ∃ n 0 ∈ N ) ( ∀ n ∈ N ) ( n ⩾ n 0 ⇒ ∣ u n − l ∣ ⩽ ε ) Exemple:
∀ n ∈ N , u n = n 3 n + 2 l = 1 3 \begin{aligned}
& \forall n \in \mathbb{N}, u_{n}=\frac{n}{3n+2} \\
& l=\frac{1}{3}
\end{aligned} ∀ n ∈ N , u n = 3 n + 2 n l = 3 1 Soit ε > 0 \varepsilon > 0 ε > 0
u n − 1 3 = n 3 n + 2 − 1 3 = 3 n − 3 n − 2 3 ( 3 n + 2 ) = − 2 3 ( 3 n + 2 ) \begin{aligned}
u_{n}-\frac{1}{3} & =\frac{n}{3n+2}-\frac{1}{3} \\
& =\frac{3n-3n-2}{3(3n+2)} \\
& =-\frac{2}{3(3n+2)}
\end{aligned} u n − 3 1 = 3 n + 2 n − 3 1 = 3 ( 3 n + 2 ) 3 n − 3 n − 2 = − 3 ( 3 n + 2 ) 2 ∣ u n − 1 3 ∣ ⩽ ε si 2 3 ( 3 n + 2 ) ⩽ ε ⇒ 1 3 n + 2 ⩽ 3 ε 2 ⇒ 3 n + 2 ⩾ 2 3 ε ⇒ n ⩾ 2 9 ε − 2 3 \begin{aligned}
\left|u_{n}-\frac{1}{3}\right| \leqslant \varepsilon \quad \text{si} \quad \frac{2}{3(3n+2)} & \leqslant \varepsilon \\
\Rightarrow \frac{1}{3n+2} & \leqslant \frac{3\varepsilon}{2} \\
\Rightarrow 3n+2 & \geqslant \frac{2}{3\varepsilon} \\
\Rightarrow n & \geqslant \frac{2}{9\varepsilon}-\frac{2}{3}
\end{aligned} ∣ ∣ u n − 3 1 ∣ ∣ ⩽ ε si 3 ( 3 n + 2 ) 2 ⇒ 3 n + 2 1 ⇒ 3 n + 2 ⇒ n ⩽ ε ⩽ 2 3 ε ⩾ 3 ε 2 ⩾ 9 ε 2 − 3 2 Posons n 0 = ( 2 9 ε − 2 3 ) + 1 n_{0}=\left(\frac{2}{9\varepsilon}-\frac{2}{3}\right)+1 n 0 = ( 9 ε 2 − 3 2 ) + 1 ∀ n ⩾ n 0 , ∣ u n − 1 3 ∣ ⩽ ε \forall n \geqslant n_{0}, \quad \left|u_{n}-\frac{1}{3}\right| \leqslant \varepsilon ∀ n ⩾ n 0 , ∣ ∣ u n − 3 1 ∣ ∣ ⩽ ε