Mathématiques - PCSI¶

Nombres complexes.¶

Lycée Lakanal 3 Avenue du Président Franklin Roosevelt 92330 Sceaux

2 Nombres complexes¶

La nature, mère des éternelles vérités, ou plutôt l’Esprit divin, est en effet trop jaloux de sa merveilleuse diversité pour permettre que toutes choses soient condensées en un seul genre. C’est pourquoi il a trouvé un détour subtil et remarquable dans ce prodige de l’analyse, ce monstre du monde des idées, cette sorte d’amphibie entre l’être et le non-être que nous appelons racine imaginaire. Leibniz

2.1 Ensemble des nombres complexes¶

On admet l’existence ${ }^{1}$ d’un ensemble noté $\mathbb{C}$ contenant $\mathbb{R}$, muni de deux opérations $(+)$ et $(\times)$ prolongeant l’addition et la multiplication des réels, et possédant un élément ${ }^{3}$ noté $i$ vérifiant $i^{2}=-1$.

Les éléments de $\mathbb{C}$ sont appelés nombres complexes et s’écrivent de manière unique sous la forme $a+b i$ où $a$ et $b$ sont des réels.

2.1.1 Le plan complexe¶

... de même qu’on peut se représenter tout le domaine des quantités réelles au moyen d’une ligne droite indéfinie, de même on peut se représenter le domaine de toutes les quantités, les réelles et les imaginaires, au moyen du plan indéfini, où chaque point déterminé par son abscisse a et par son ordonnée $b$ représente en même temps la quantité a+ib. Gauss, 1811

• Plan complexe. Le plan étant rapporté à un repère orthonormé direct ( $O, \overrightarrow{\mathrm{e}_{1}}, \overrightarrow{\mathrm{e}_{2}}$ ), à tout point $M(a, b)$ on associe le nombre complexe $z=a+b i$

Réciproquement, à tout nombre complexe $z=a+b i$ on peut faire correspondre le point $M$ du plan de coordonnées $(a, b)$ ou le vecteur $\vec{u}$ de coordonnées $(a, b)$ dans la base $\left(\overrightarrow{\mathrm{e}_{1}}, \overrightarrow{\mathrm{e}_{2}}\right)$.

On dit que $z$ est l’affixe du point $M$ ou du vecteur $\vec{u}$ et que $M$ (ou $\vec{u}$ ) est l’image du nombre complexe $z$.

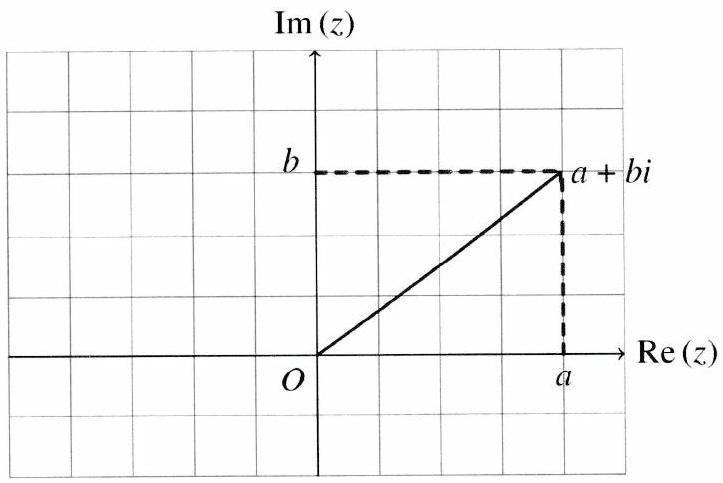
^[2]On a donc une correspondance entre l’ensemble $\mathbb{C}$ des nombres complexes et l’ensemble des points du plan ou des vecteurs du plan

Remarque. La notation $\mathbb{R}^{2}$ ou $\mathbb{R} \times \mathbb{R}$ désigne l’ensemble des couples ( $a, b$ ) où $a \in \mathbb{R}$ et $b \in \mathbb{R}$. Le plan ainsi utilisé pour représenter géométriquement les nombres complexes sera appelé plan complexe.

• Partie réelle et partie imaginaire d’un nombre complexe.

Définition. Soit $z=a+b i$ un nombre complexe. Les nombres $a$ et $b$ s’appellent respectivement la partie réelle et la partie imaginaire du nombre complexe $z$. On les note $\operatorname{Re}(z)$ et $\operatorname{Im}(z)$.

Si $\operatorname{Re}(z)=0$, on dit que le nombre complexe $z$ est imaginaire pur. — Un nombre complexe $z$ est réel si et seulement si $\operatorname{Im}(z)=0$.

• Un nombre complexe est imaginaire pur si et seulement si $\operatorname{Re}(z)=0$.

• Axe réel et axe imaginaire. L’axe ( $O, \overrightarrow{\mathrm{e}_{1}}$ ) du plan complexe est appelé axe réel et l’axe $\left(O, \overrightarrow{\mathrm{e}_{2}}\right)$, axe imaginaire.

• Forme algébrique (ou cartésienne) d’un nombre complexe.

Définition. L’écriture $a+b i$ d’un nombre complexe $z$ s’ appelle forme algébrique de $z$.

Cette écriture est unique : en effet, si $a+b i=a^{\prime}+b^{\prime} i$ alors $a-a^{\prime}=\left(b^{\prime}-b\right) i$ et en élevant au carré chaque membre, on obtient $\left(a-a^{\prime}\right)^{2}+\left(b^{\prime}-b\right)^{2}=0$. Une somme de réels positifs n’est nulle que si chacun des termes de cette somme est nul, donc $a-a^{\prime}=0$ et $b^{\prime}-b=0$, donc $a=a^{\prime}$ et $b=b^{\prime}$.

2.1.2 Opérations dans $\mathbb{C}$¶

• addition de deux nombres complexes : Soient $z_{1}$ et $z_{2}$ deux nombres complexes. Le nombre complexe $z_{1}+z_{2}$ est déterminé par l’égalité

• multiplication d’un nombre complexe par un nombre réel : Soient $\lambda \in \mathbb{R}$ et $z \in \mathbb{C}$. Le nombre complexe $\lambda z$ est déterminé par

• définition de la multiplication : Soient $z_{1}$ et $z_{2}$ deux nombres complexes. Le nombre complexe $z_{1} \times z_{2}$ est déterminé par l’égalité

Exercice 1. Exprimer en fonction de $x, y, x^{\prime}, y^{\prime}$ les parties réelles et imaginaires des nombres complexes : $A=(x+y i)\left(x^{\prime}+y^{\prime} i\right), \quad B=(x+y i)^{3}, \quad C=(y+x i)(x+y i)$.

2.1.3 Conjugaison. Module¶

- Conjugué d’un nombre complexe.¶

Définition. Le conjugué du nombre complexe $z=a+b i$ est le nombre complexe $a-b i$ et est noté $\bar{z}$.

Proposition. Un nombre complexe $z$ est réel si et seulement si $z=\bar{z}$.

Proposition. Soit $z, z^{\prime}$ deux nombres complexes. Alors

Proposition. Pour tout $z \in \mathbb{C}$,

Exemple. Mettre sous forme cartésienne le nombre $\frac{3+6 i}{3-4 i}$.

Exercice 2. Discuter, suivant les réels $a, b, c$, les solutions de l’équation $a z+b \bar{z}+c=0$.

- Module d’un nombre complexe.¶

Proposition. Soit $z=a+b i$ un nombre complexe. Alors

Définition. La quantité $z \bar{z}$ est positive et on appelle module de $z$ la quantité $\sqrt{z \bar{z}}$ qui est notée $|z|$. Lorsque $z=a+b i$, on a donc $|z|^{2}=z \bar{z}=a^{2}+b^{2}$ et $|z|=\sqrt{a^{2}+b^{2}}$.

Remarque. Soit $z$ un nombre complexe non nul : $\frac{1}{z}=\frac{1}{|z|^{2}} \bar{z}$. En particulier, si $|z|=1$ alors $\frac{1}{z}=\bar{z}$.

Proposition. Pour tout $z \in \mathbb{C}, \quad|\bar{z}|=|z|$.

Proposition. Pour tout $z \in \mathbb{C}, \quad|\operatorname{Re}(z)| \leq|z|$ et $|\operatorname{Im}(z)| \leq|z|$

Remarque. On a l’équivalence : $\operatorname{Re}(z)=|z|$ si et seulement si $z \in \mathbb{R}^{+}$.

Proposition. Soient $z$ et $z^{\prime}$ deux nombres complexes. Alors (1) $\left|z z^{\prime}\right|=|z| \times\left|z^{\prime}\right|$, (2) $\left|\frac{z}{z^{\prime}}\right|=\frac{|z|}{\left|z^{\prime}\right|}$ (lorsque $z^{\prime} \neq 0$ ), (3) $\left|z+z^{\prime}\right| \leq|z|+\left|z^{\prime}\right|$ (première inégalité triangulaire). (4) $\left|z+z^{\prime}\right|=|z|+\left|z^{\prime}\right|$ ssi $z=0$ ou il existe $k \in \mathbb{R}^{+}$tel que $z^{\prime}=k z$. (5) $\left\|z^{\prime}\left|-\left|z \| \leq\left|z^{\prime}-z\right|\right.\right.\right.$.

Corollaire. Soit $n \in \mathbb{N}$ tel que $n \geq 2$. Pour tous nombres complexes $z_{1}, z_{2}, \ldots, z_{n}$, (1) $\left|\prod_{i=1}^{n} z_{i}\right|=\prod_{i=1}^{n}\left|z_{i}\right|$ (2) $\left|\sum_{i=1}^{n} z_{i}\right| \leq \sum_{i=1}^{n}\left|z_{i}\right| \quad$ (inégalité triangulaire généralisée)

Exercice 3. Montrer que quelques soient les nombres complexes $u, v \in \mathbb{C}$,

2.1.4 Argument d’un nombre complexe. Notation exponentielle.

• Argument d’un nombre complexe. Le plan étant rapporté à un repère orthonormé direct $(0, \vec{u}, \vec{v})$, à tout nombre complexe $z$ non nul, on peut associer l’angle orienté ( $\vec{u}, \overrightarrow{O M}$ ) où $M$ est l’image de $z$.

Si $\theta \in \mathbb{R}$ est une mesure de cet angle orienté alors tout réel de la forme $\theta+2 k \pi, k \in \mathbb{Z}$ est aussi une mesure de l’angle orienté.

Réciproquement, si $\theta^{\prime} \in \mathbb{R}$ est une autre mesure de l’angle orienté il existe $k \in \mathbb{Z}$ tel que $\theta^{\prime}=\theta+2 k \pi$.

Définition. Soit $x, x^{\prime}$ deux réels. S’il existe $m \in \mathbb{Z}$ tel que $x^{\prime}=x+2 m \pi$, on dit que $x$ et $x^{\prime}$ sont congrus modulo $2 \pi$ et on note $x \equiv x^{\prime} \bmod (2 \pi)$.

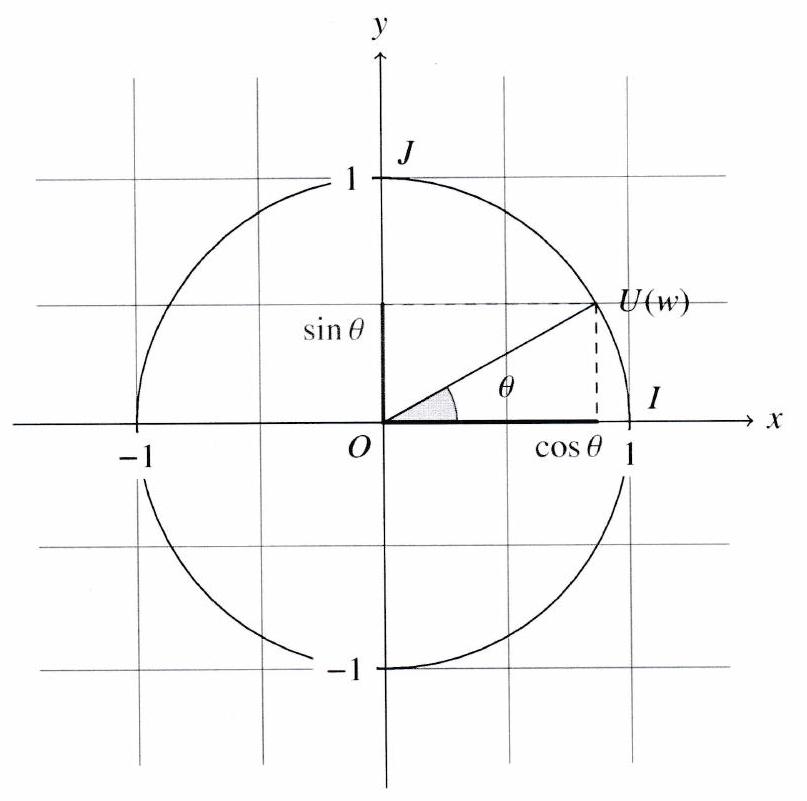
Définition. On appelle argument de $z \neq 0$ et on note $\arg (z)$ une mesure quelconque de l’angle orienté ( $\vec{u}, \overrightarrow{O M}$ ) où $M$ est l’image de $z$.

Le nombre complexe $w=\frac{z}{|z|}$ est de module 1 et son image $U$ est donc situé sur le cercle trigonométrique. Comme les vecteurs $\overrightarrow{O M}$ et $\overrightarrow{O U}$ sont colinéaires de même sens, les angles orientés $(\vec{u}, \overrightarrow{O M})$ et $(\vec{u}, \overrightarrow{O U})$ sont égaux. Il existe donc $k \in \mathbb{Z}$ tel que

• Forme trigonométrique et notation exponentielle. Si $\theta=\arg (z)$ alors $\theta$ est aussi un argument de $w$ et le point $U$ a pour coordonnées $(\cos \theta, \sin \theta)$. On peut donc écrire $w= \cos \theta+(\sin \theta) i$ de sorte que $z=|z|(\cos \theta+(\sin \theta) i)$ où $\theta$ est un argument de $z$.

Définition. L’écriture précédente du nombre complexe $z$

où $\theta$ est un argument de $z$, s’ appelle la forme trigonométrique ou polaire de $z$.

Un nombre complexe est caractérisé par son module et par l’un de ses arguments.

Théorème. Deux nombres complexes non nuls sont égaux si et seulement si ils ont même module et si leurs arguments sont congrus modulo $2 \pi$. Etant donné deux nombres complexes non nuls $z$ et $z^{\prime}$,

Remarque. Un argument de $z$ désignera l’une quelconque de ces mesures, alors que l’argument de $z$ désigne la classe de toutes les mesures de l’angle orienté. Parmi toutes ces mesures, il en existe une et une seule dans tout intervalle de la forme $[a, a+2 \pi]$ où $a$ est un nombre réel. La mesure de l’angle orienté ( $\vec{u}, \overrightarrow{O M}$ ) comprise dans l’intervalle [ $0,2 \pi[$ s’appelle l’argument principal de $z$.

Pour $t \in \mathbb{R}$, on note $\mathrm{e}^{\mathrm{i} t}$ le nombre complexe $\cos t+(\sin t) i$.

- Nombre complexe de module 1.¶

L’ensemble des nombres complexes de module 1 est noté $\mathbb{U}$. Il vérifie :

• $\forall z \in \mathbb{U}, \forall z^{\prime} \in \mathbb{U}: z z^{\prime} \in \mathbb{U}$ (U est stable par produit)

• $\forall z \in \mathbb{U}: \bar{z} \in U$ (U est stable par conjugaison)

• $\forall z \in \mathbb{U}: \frac{1}{z} \in \mathbb{U}$ (U est stable par inverse)

Proposition. Soit $z \in \mathbb{C}$. Alors on dispose de l’équivalence : $z \in \mathbb{U}$ ssi il existe $\theta \in \mathbb{R}$ tel que $z=\mathrm{e}^{i \theta}$.

Remarque. Attention, il n’y a pas unicité du réel $\theta$. Pour tous réels $\theta$ et $\theta^{\prime}$ :

• $\mathrm{e}^{i \theta}=\mathrm{e}^{i \theta^{\prime}} \operatorname{ssi} \theta \equiv \theta^{\prime} \bmod (2 \pi)$

• $\mathrm{e}^{i \theta} \mathrm{e}^{i \theta^{\prime}}=\mathrm{e}^{i\left(\theta+\theta^{\prime}\right)}, \quad \frac{1}{\mathrm{e}^{i \theta}}=\mathrm{e}^{-i \theta}, \quad \frac{\mathrm{e}^{i \theta}}{\mathrm{e}^{i \theta^{\prime}}}=\mathrm{e}^{i\left(\theta-\theta^{\prime}\right)}$

• $\overline{\mathrm{e}^{i \theta}}=\mathrm{e}^{-i \theta}$

- La formule d’Abraham de Moivre ${ }^{4}$¶

Proposition. Formule de Moivre.¶

(1) Pour tout $n \in \mathbb{N}$, et tout $t \in \mathbb{R},(\cos t+(\sin t) i)^{n}=\cos n t+(\sin n t) i$. (2) On a $(\cos t+(\sin t) i)^{-1}=\frac{1}{\cos t+(\sin t) i}=\cos (-t)+(\sin (-t)) i$ (3) Pour tout $n \in \mathbb{Z}$, et tout $t \in \mathbb{R},(\cos t+(\sin t) i)^{n}=\cos n t+(\sin n t) i$.

Si $z$ est un nombre complexe non nul et si $\theta$ est un de ses arguments alors la forme trigonométrique de $z$ s’ écrit donc aussi $z=|z| \mathrm{e}^{i \theta}$.

La forme trigonométrique d’un nombre complexe fournit le module et un argument de ce nombre complexe : si $z=r(\cos t+(\sin t) i)$ où $r \in \mathbb{R}, r>0$ et $\theta \in \mathbb{R}$ alors $|z|=r$ et $\theta$ est un argument de $z$.

Soit $\theta$ et $\theta^{\prime}$ deux réels. On a alors :

^[1]

Proposition. Soit $z, z^{\prime}$ deux nombres complexes non nuls s’écrivant sous forme trigonométrique $z=|z| \mathrm{e}^{i \theta}, z^{\prime}=\left|z^{\prime}\right| \mathrm{e}^{i \theta^{\prime}}$. Alors

Conséquence. Soient $z, z^{\prime} \in \mathbb{C}, z \neq 0, z^{\prime} \neq 0$ et $n \in \mathbb{N}^{*}$.

Exercice 4. Soient $u=\frac{\sqrt{6}-i \sqrt{2}}{2}$ et $v=1-i$. Calculer le module et un argument de $u$ et $v$. En déduire le module et un argument de $w=\frac{u}{v}$.

Exercice 5. Soit $z$ le nombre complexe $\frac{1+i \sqrt{3}}{1+i}$. Dire en justifiant si chacune des affirmations est vraie ou fausse. (a) $\overline{\left(\frac{1}{z^{12}}\right)}=\frac{1}{64}$ (b) $z^{30}=2^{15}$ (c) $(i z)^{15} \in \mathbb{R}$ (d) pour tout $k \in \mathbb{N}^{*}, z^{12 k} \in \mathbb{R}$

2.1.5 Exemples et applications¶

- Formules d’Euler. ${ }^{5}$¶

5. Leonhard Euler, 1707-1783. Fils d’un pasteur élève de Jakob Bernoulli, il fait de brillantes études de philosophie et reçoit des cours particuliers de Johann Bernoulli. Il part à St Petersbourg en 1727, où il obtient (sur recommandation de Daniel Bernoulli) une chaire de philosophie naturelle en 1730 et la chaire de mathématiques (abandonnée par D. Bernoulli) en 1733. Il perd l’oeil droit à cause du climat rude du pays en 1735. En 1741, il est nommé directeur de la section mathématiques et physique à l’académie des sciences de Berlin et Frederick II dira : « J’ai ici un gros cyclope de géomètre... il ne reste plus qu’un oeil à notre homme, et une courbe nouvelle, qu’il calcule à présent, pourrait le rendre aveugle tout à fait. » En 1732, il montre que le nombre de Fermat $F_{5}=2^{2^{5}}+1$ et le nombre de Mersenne $M_{31}=2^{31}-1$ ne sont pas premiers. Il prouve la généralisation du (petit) théorème de Fermat : si $a$ et $m$ sont premiers entre eux alors $a^{\phi(m)}-1$ est divisible par $m$ où $\phi(m)$ est le nombre d’entiers naturels inférieurs à $m$ qui sont premiers avec $m$ ( $\phi$ est dite fonction d’Euler). Il note e la base du logarithme népérien : «ubi e denotat numerum, cuius logarithmus hyperbolicus est $1 \gg$ (Mechanica, 1736). En 1738, il montre le théorème de Fermat pour les valeurs $n=3,4$. Euler apporte une contribution principale à l’évolution de la notion de fonction : il est le premier à regarder une fonction comme la donnée d’une courbe dans un repère possédant un unique point d’intersection avec les droites verticales et développa les deux points de vues en parallèle. Il développe l’idée de Johann Bernouilli selon laquelle la trigonométrie est une branche de l’analyse et montre que les fonctions sin, cos et exp sont reliées par la formule qui porte son nom :

2. La notation $i$ est due à Euler en 1777 et est reprise ensuite par Gauss.