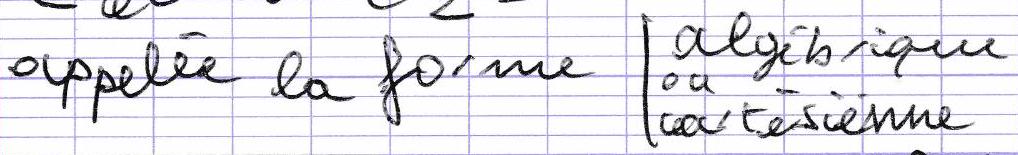Chapitre 2: nombres complexes
Chapitre 2: nombres complexes¶
Ensemble des nombres complexes¶
Existence admise:¶
Notation: C
Tout nombre complexe z∈C s’écrit sous la forme z=a+bi où a∈R,b∈R et i2=−1. Cette écriture est
partie réelle. ↑ de z notée Re(z), partie imaginaire de z notée Im(z)
Représentation dans le plan complexe
φ:R2→C
(a;b)↦a+bi
est une bijection
MS’ appelle image du nombre complexe z dans le plan complexe z=a+bi est appelé affixe du point M(a,b)
On peut aussi voir les éléments du plan comme des vecteurs et dans ce cas: OM est le vecteur image du nombre complexe z=a+bi
L’axe (0,u): axe réel
L’axe (0,v): axe imaginaire
L’écriture z=a+bi d’un nombre complexe est
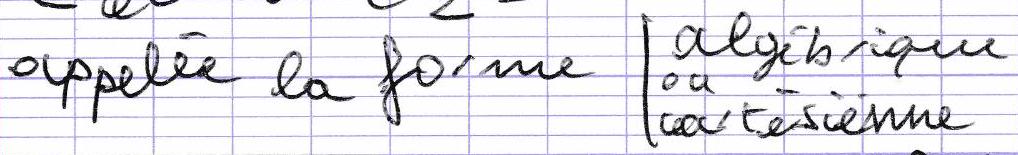
z=z′ ssi {Re(z)=Re(z′)Im(z)=Im(z′) Opérations
Soit z=a+bi∈C
z′=a′+b′i∈C z+z′:=(a+a′)+(b+b′)i
Re(z+z′)=Re(z)+Re(z′)Im(z+z′)=Im(z)+Im(z′) z×z′=(a+bi)×(a′+b′i)=(aa′−bb′)+(ab′+a′b)i Exemple:¶
(1+i3)3=1+33i−3−33i=−8
(a+bi)(a−bi)=a2+b2
1+i2+3i=2(2+3i)(1−i)=22−2i+3i+3=25+i=25+21i
Conjugaison
Soit z=a+bi∈C
Le conjugué de z est: zˉ=a−bi
La conjugaison est l’application $\sigma: \left\l...