Circuits du second ordre¶

Exercice 1 : Caractéristiques de signaux sinusoïdaux -¶

1. Donner l’amplitude, la période, la fréquence et la phase initiale des signaux suivants. Le temps est exprimé en secondes. (a) $s_{1}(t)=15 \cos (100 \pi t+0,5)$; (b) $s_{2}(t)=5 \sin \left(7,854 \cdot 10^{6} \times t\right)$; (c) $s_{3}(t)=2 \sin \left(120 \pi t-\frac{\pi}{4}\right)$; (d) $s_{4}(t)=15 \cos (200 \pi t)-5 \sin (200 \pi t)$.

Aide : pour $s_{4}(t)$, on pourra mettre $\sqrt{15^{2}+5^{2}}$ en facteur. 2. Donner la phase initiale d’un signal sinusoïdal de période $T$ qui, à l’instant $t=\frac{T}{4}$, vaut la moitié de sa valeur maximale et est croissant.

Exercice 2 : Circuit $L C$ série - ★¶

On étudie le circuit ci-contre. Pour $t<0$, le condensateur est déchargé. À l’instant $t=0$, on ferme l’interrupteur, ce qui connecte le générateur idéal de f.é.m $E$ constante au condensateur et à la bobine.

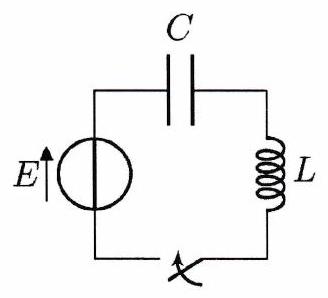
1. Établir l’équation différentielle vérifiée par l’intensité du courant dans le circuit.

2. Identifier la pulsation propre du circuit.

3. Résoudre l’équation différentielle compte tenu des conditions initiales.

4. En déduire l’expression de la tension aux bornes du condensateur.

5. Représenter les allures de $u_{c}(t)$ et $i(t)$.

Exercice 3 : Circuit $L C$ parallèle¶

On étudie le circuit ci-contre. Pour $t<0$, le condensateur est déchargé et aucun courant ne circule dans le circuit. À l’instant $t=0$, on ferme l’interrupteur, ce qui connecte le générateur idéal de courant en parallèle avec le condensateur et la bobine.

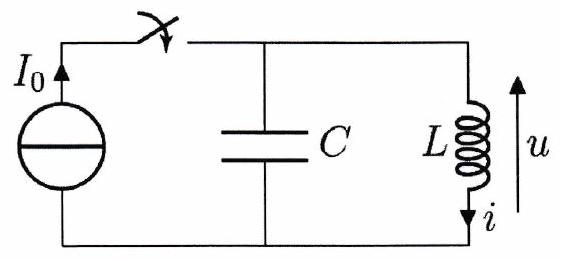
1. Établir l’équation différentielle vérifiée par l’intensité $i$.

2. Identifier la pulsation propre du circuit.

3. Justifier très proprement $i\left(t=0^{+}\right)$et $u\left(t=0^{+}\right)$. Puis en déduire $\frac{\mathrm{d} i}{\mathrm{~d} t}\left(t=0^{+}\right)$.

4. Résoudre complètement l’équation différentielle compte tenu des conditions initiales.

5. Représenter l’allure de $i$ en fonction du temps.

Exercice 4 : Étude du régime permanent -¶

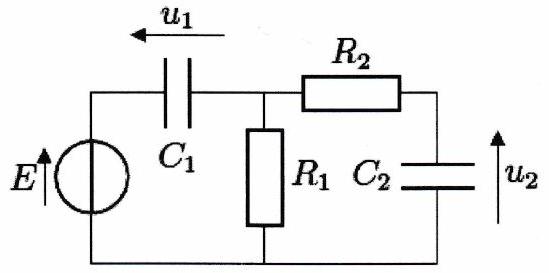
Déterminer les différentes intensités et tensions ( $u, i, u_{1}, u_{2}$ ) indiquées ci-dessous lorsque le régime permanent est atteint.

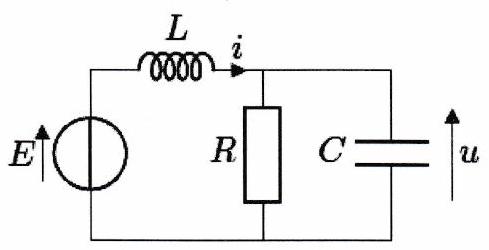
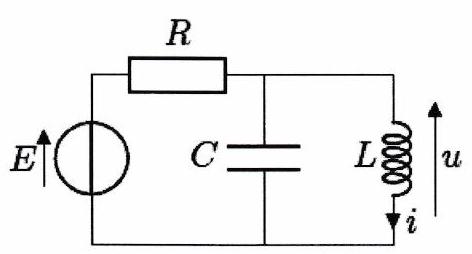
Exercice 5 : Oscillations et facteur de qualité - ★¶

On considère un circuit $R L C$ série peu amorti, de pulsation propre $\omega_{0}$ et de facteur de qualité $Q$. L’expression de la tension $u_{C}(t)$ aux bornes du condensateur est donnée par :

1. Rappeler les dimensions et unités de $\tau$ et $\Omega$. Établir leurs expressions en fonction de la pulsation propre $\omega_{0}$ et du facteur de qualité $Q$, puis en fonction de $R, L$ et $C$.

2. Que peut-on dire de la pseudo-période des oscillations dans le cas où $Q \gg 1$ ?

3. On suppose que les oscillations restent visibles tant que leur amplitude reste supérieure à $5 \%$ de l’amplitude initiale. Exprimer la durée $T_{5 \%}$ pendant laquelle les oscillations sont visibles, en fonction de $\omega_{0}$ et $Q$.

4. En déduire l’expression du nombre $N$ d’oscillations observées pendant le régime transitoire en fonction du facteur de qualité.

Exercice 6 : Lecture graphique - ★¶

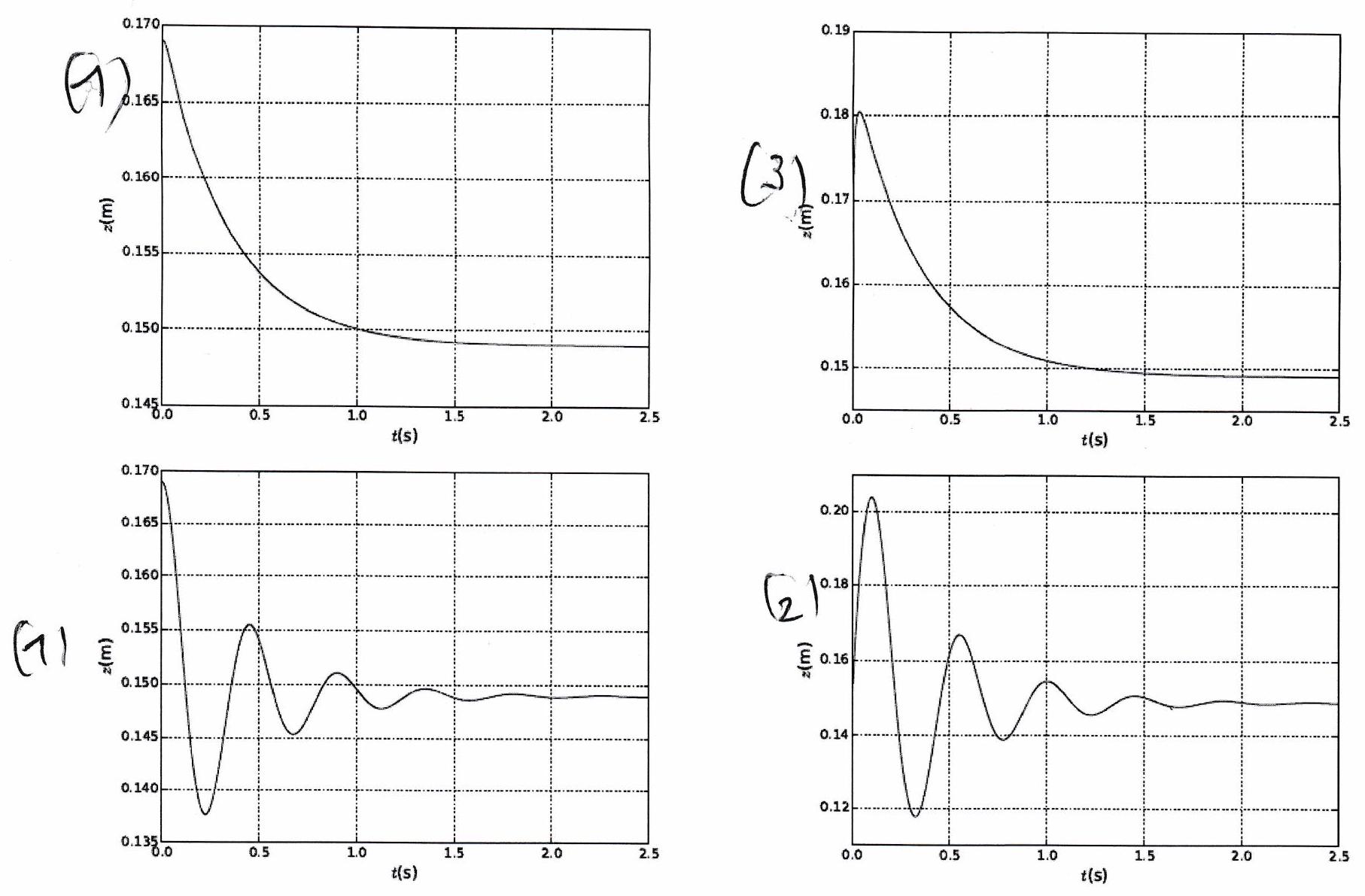
Associer à chaque graphe, le jeu de conditions initiales et le jeu de paramètre correspondant, ci-dessous.

• Les conditions initiales :

1. $z(0)=z_{\text {éq }}+2,0 \mathrm{~cm}$ $\dot{z}(0)=0 \mathrm{~m} / \mathrm{s}$

2. $z(0)=z_{\text {éq }}$ $\dot{z}(0)=1 \mathrm{~m} / \mathrm{s}$

3. $z(0)=z_{\text {éq }}+2,0 \mathrm{~cm}$ $\dot{z}(0)=1 \mathrm{~m} / \mathrm{s}$

• Les paramètres : a) $k=20 \mathrm{~N} \cdot \mathrm{~m}^{-1} ; m=0,1 \mathrm{~kg} ; \lambda=0,5 \mathrm{~kg} \cdot \mathrm{~s}^{-1}$ b) $k=20 \mathrm{~N} \cdot \mathrm{~m}^{-1} ; m=0,1 \mathrm{~kg} ; \lambda=7 \mathrm{~kg} \cdot \mathrm{~s}^{-1}$

Exercice 7 : Connexion d’une bobine à un circuit RC parallèle - ★★¶

Le circuit représenté ci-contre est alimenté depuis très longtemps par un générateur de tension continu de f.é.m. $E$ et de résistance interne $R$. À $\mathrm{t}=0$, on ferme l’interrupteur et on suit à l’oscilloscope l’évolution de la tension $u(t)$ aux bornes du circuit $R L C$ parallèle ainsi obtenu.

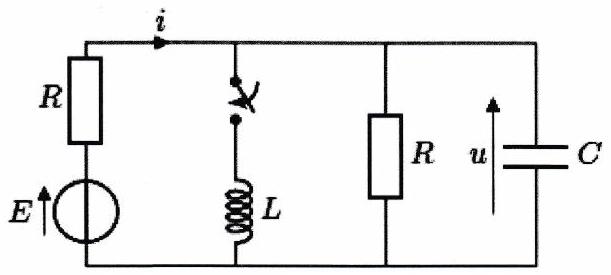
On donne quelques valeurs : $E=5 \mathrm{~V}, R=10 \mathrm{k} \Omega$ et $C=100 \mathrm{nF}$.

1. Donner la valeur de $u\left(t=0^{+}\right)$. Justifier.

2. Donner la valeur vers laquelle doit tendre $u(t)$ en régime permanent. Justifier.

3. Montrer que $\frac{\mathrm{d} u}{\mathrm{~d} t}\left(t=0^{+}\right)=0$.

4. Établir, l’équation différentielle vérifiée par $u(t)$ après la fermeture de l’interrupteur. L’écrire sous sa forme canonique et donner l’expression de la pulsation propre $\omega_{0}$ et du facteur de qualité $Q$.

5. Établir une inégalité vérifiée par $R, L$ et $C$ pour que l’on observe un régime pseudopériodique. On suppose cette inégalité vérifiée pour la suite.

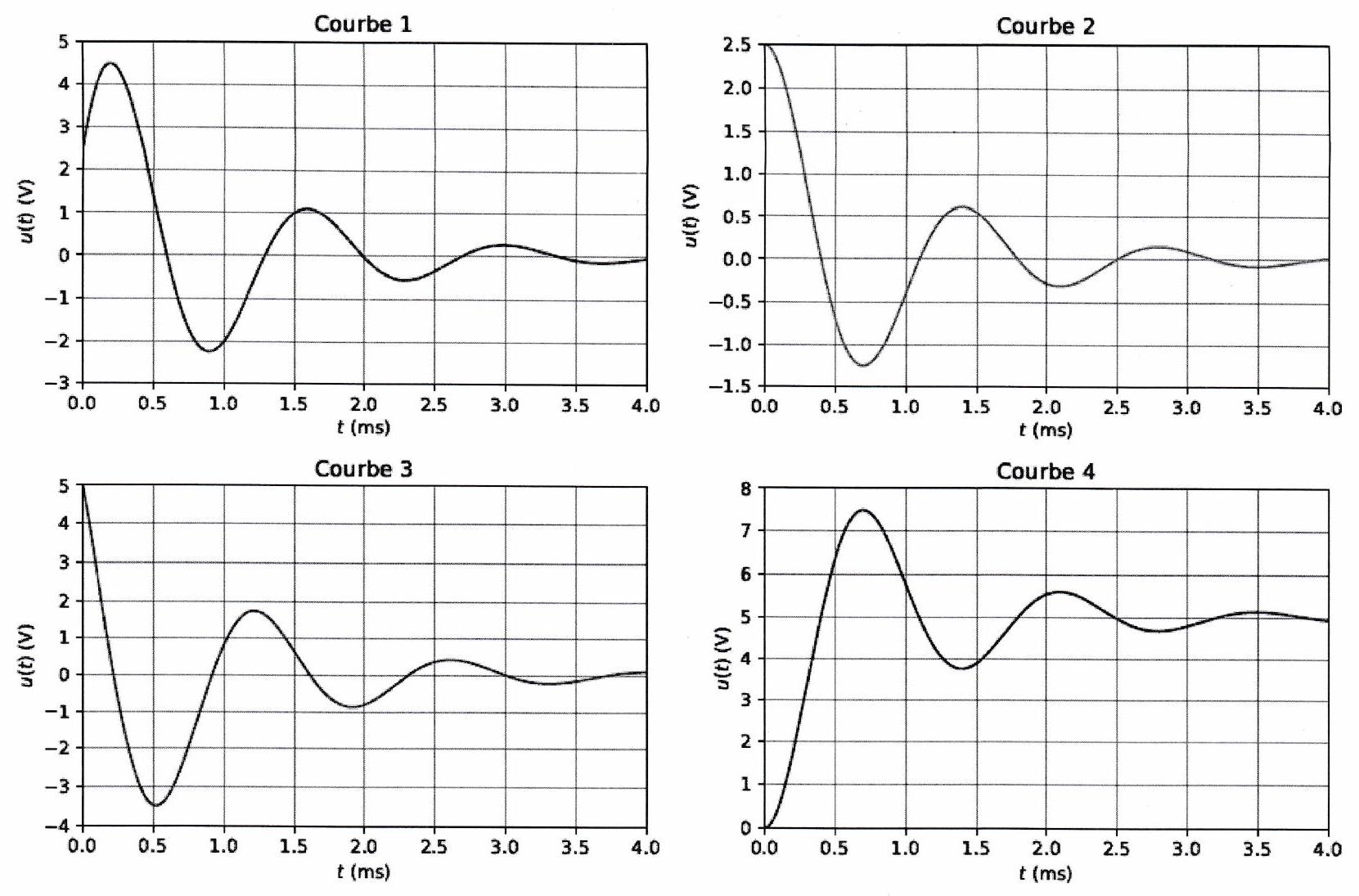
6. Parmi les courbes représentées ci-dessous, identifier celle qui convient. Justifier.

7. Représenter l’allure de $i(t)$, sans établir ni résoudre d’équation différentielle.

8. Proposer une estimation de la valeur de l’inductance $L$.

9. Résoudre l’équation différentielle pour donner l’expression de $u(t)$ pour $t>0$.

Exercice 8 : Pont de Wien - ★★¶

On considère le circuit représenté ci-contre en $t=0^{-}$. L’interrupteur est initialement ouvert et le condensateur $C^{\prime}$ est chargé sous une tension $U_{0}=3 \mathrm{~V}$ tandis que le condensateur $C$ est déchargé.

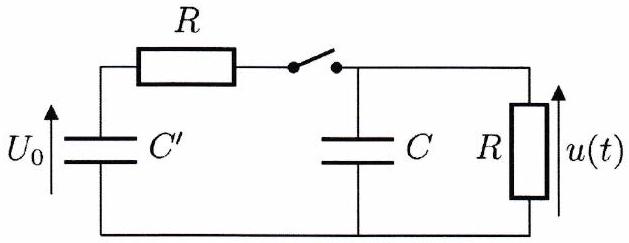
La capacité des deux condensateurs est la même $C=C^{\prime}=100 \mathrm{nF}$. On prend $R=10 \mathrm{k} \Omega$ et on pose $\tau=R C$. À l’instant $t=0$, on ferme l’interrupteur.

1. Déterminer sans calcul les valeurs de la tension $u(t)$ pour $t=0^{+}$et lorsque le régime permanent est atteint, c’est-à-dire quand $t \rightarrow \infty$.

2. Montrer que l’équation différentielle vérifiée par $u(t)$ pour $t \geq 0$ est :

Préciser la valeur du facteur de qualité $Q$. 3. La résoudre pour exprimer $u(t)$ pour $t \geq 0$ et représenter graphiquement $u(t)$. 4. Déterminer l’instant $t_{m}$ pour lequel $u(t)$ passe par un maximum.

Exercice 9 : Régime pseudo-périodique - ★★¶

On considère un circuit composé d’une résistance $R$, d’une bobine d’inductance $L$ et d’un condensateur de capacité $C$. On soumet le circuit à un échelon de tension tel que :

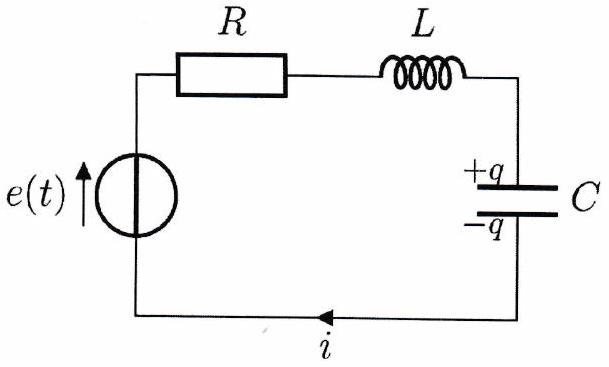
1. Justifier qu’à $t=0^{-}$, la charge $q$ et l’intensité $i$ sont nulles.

2. Établir l’équation différentielle vérifiée par la charge $q$ du condensateur pour $t>0$. On posera $\omega_{0}=\frac{1}{\sqrt{L C}}$ et $\gamma=\frac{R}{2 L}$.

3. Donner les valeurs de $q$ et de sa dérivée première en $t=0^{+}$. Justifier.

4. Donner la condition portant sur $\omega_{0}$ et $\gamma$ pour laquelle on observe un régime transitoire pseudo-périodique. On supposera cette condition vérifiée pour la suite.

5. Montrer que l’expression de la charge pour $t>0$ peut se mettre sous la forme $q(t)= (A \cos (\omega t)+B \sin (\omega t)) e^{-\gamma t}+D$, où on exprimera $\omega, A, B$ et $D$ en fonction de $C, E, \omega_{0}$ et $\gamma$.

6. Exprimer l’intensité $i(t)$ dans le circuit pour $t>0$ en fonction de $C, E, \omega_{0}$ et $\gamma$.

7. Quelles sont les valeurs atteintes par $q(t)$ et $i(t)$ après le régime transitoire? Justifier par des considérations simples.

Exercice 10 : Réponse d’un circuit $R L C-\star \star \star$¶

Le circuit représenté ci-contre est alimenté par un générateur de tension continu de f.é.m. E. On suppose que l’interrupteur est ouvert depuis très longtemps. À l’instant $t=0$, on ferme l’interrupteur.

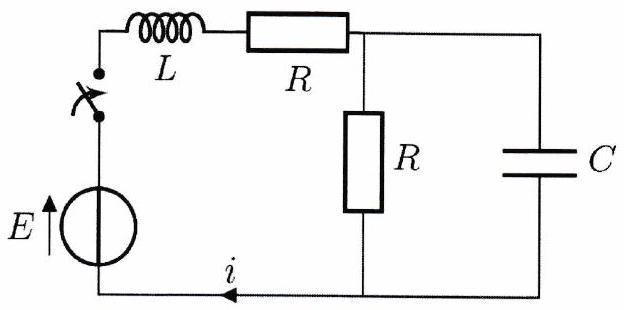
On suppose que $R C=L / R=\tau$. Exprimer l’intensité $i(t)$ du courant pour $t>0$.