Circuits du second ordre
Circuits du second ordre¶
La conservation de l’énergie observée pour l’oscillateur harmonique ne s’applique pas aux systèmes réels. En pratique, les oscillations finissent par s’amortir car il existe toujours des mécanismes dissipatifs.
I) Approche expérimentale¶
Expérience 1 : Circuit série soumis à un échelon de tension¶
À quoi ressemble le régime transitoire dans un circuit ? A-t-il toujours la même allure si l’on change les valeurs des composants ?
oscilloscope ;
boite à décades ;
bobine 1000/500 spires;
GBF ;
boite à décades ;
fils.
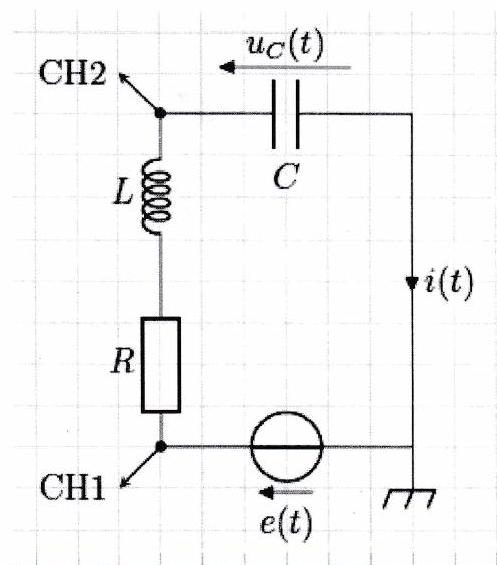
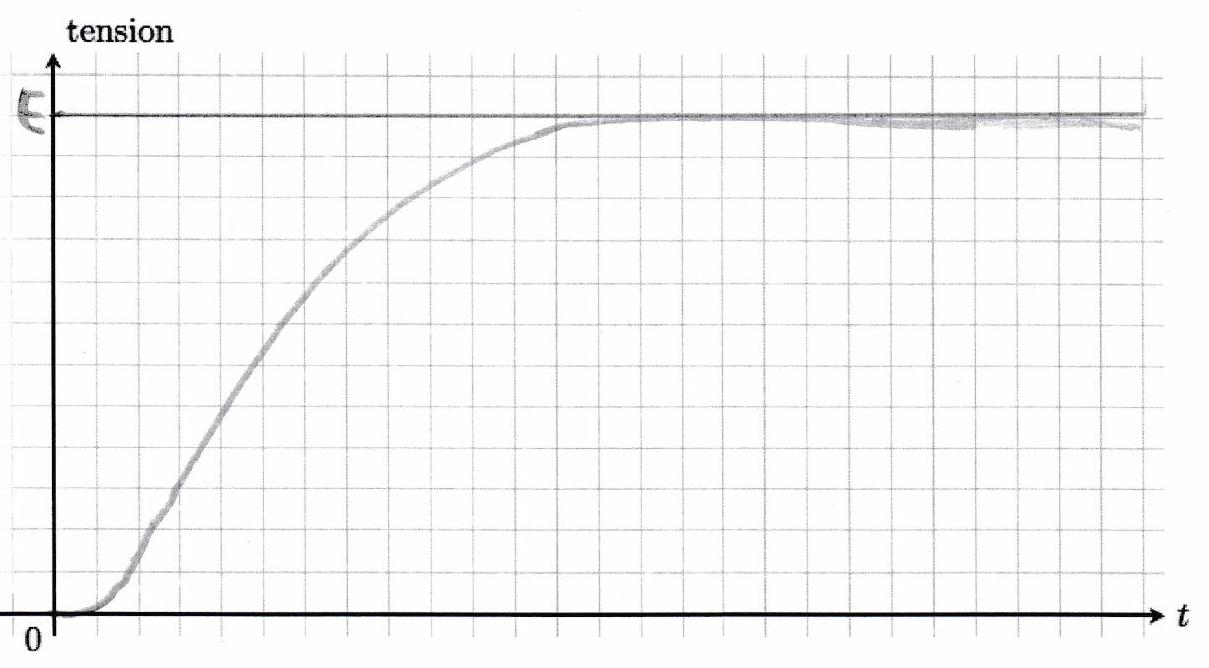
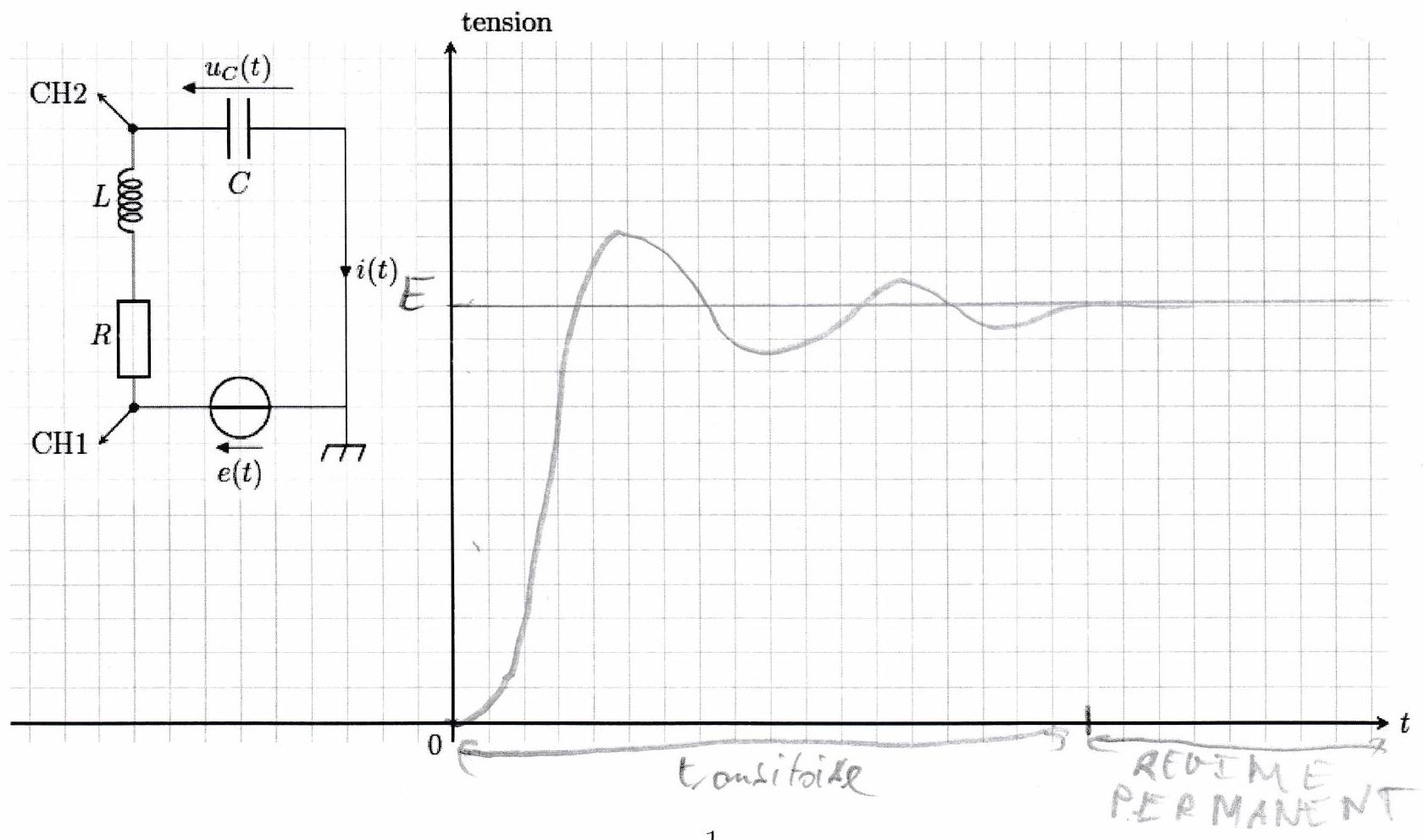
Comme dans le chapitre précédent, on peut distinguer deux régimes :
le régime transitoire ;
le régime permanent.
Pour certaines valeurs de résistance, capacité et inductance, le régime transitoire semble proche de celui d’un circuit du premier ordre, mais pour d’autres, il peut présenter des oscillations. Le choix des composants semble influencer :
la nature du régime transitoire, oscillant ou non ;
la durée du régime transitoire ;
la pseudo-période des oscillations.
Remarque¶
Plus la résistance est importante, plus les pertes Joules sont importantes donc plus le système est amorti. Les oscillations diminue voire disparaissent quand on augmente la résistance.
II ) Circuit série, Mise en équation¶
Exercice de cours à connaître 1¶
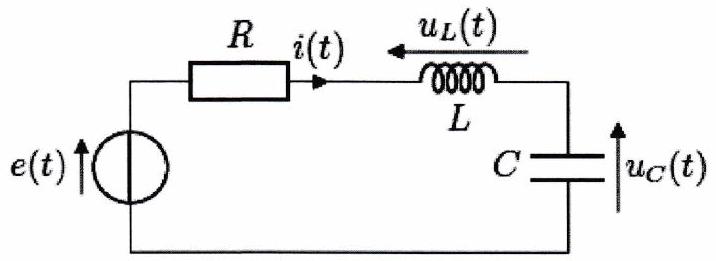
On considère le circuit série représenté ci-contre. Le générateur impose un échelon de tension parfait, c’est-à-dire :
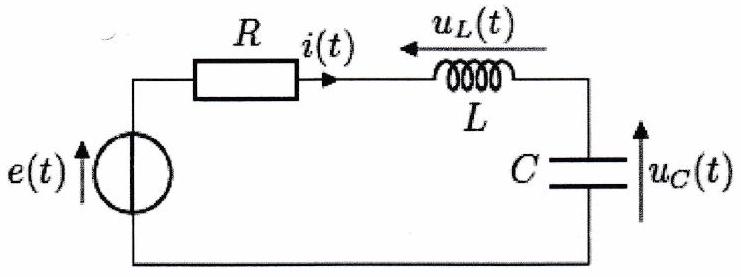
Établir l’équation différentielle vérifiée par la tension pour .
L’écrire sous sa forme canonique :
Donner l’expression de la pulsation propre et du facteur de qualité . 3. Quelle est la dimension de ?
Définition 1 : Oscillateur amorti¶
L’équation associée à un oscillateur amorti de pulsation propre et de facteur de qualité s’écrit sous forme canonique
Dans un circuit série, la tension aux bornes du condensateur , sa charge et l’intensité du courant dans le circuit vérifient l’équation d’un oscillateur amorti de pulsation propre et de facteur de qualité , avec
Remarque¶
L’expression du facteur de qualité n’est valable que pour un circuit série !
Dans l’équation sous sa forme canonique, la constante devant la dérivée première est positive : il s’agit d’un terme d’amortissement, de modération qui assure la convergence de la solution. Sinon, il s’agirait d’un terme d’amplification qui mènerait à une divergence inquiétante de la solution.
Dans le cas où l’amortissement est négligeable, c’est-à-dire quand , soit , on retrouve bien l’équation de l’oscillateur harmonique.
III ) Différents régimes de fonctionnement¶
Trouver les solutions de l’équation homogène d’un oscillateur amorti de pulsation propre et de facteur de qualité
revient à trouver les racines du polynôme caractéristique associé à l’équation différentielle homogène, c’est-à-dire les solutions de l’équation :
Seules les solutions réelles de l’équation homogène nous intéressent, mais leur forme dépend de la nature des racines du polynôme caractéristique, que l’on déterminera dans . Le discriminant de l’équation caractéristique s’écrit
et on distingue trois cas suivant son signe.
Remarque¶
L’expression des racines du polynôme caractéristique n’est pas à apprendre par cœur mais doit pouvoir être retrouvée rapidement. En revanche, la forme des solutions de l’équation homogène doit être connue dans les trois cas.
A) Régime transitoire apériodique¶
Si le discriminant est strictement positif, c’est-à-dire si , le polynôme caractéristique admet deux racines réelles et négatives
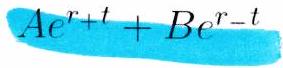
Si , le régime transitoire est apériodique. La solution générale de l’équation homogène est alors de la forme
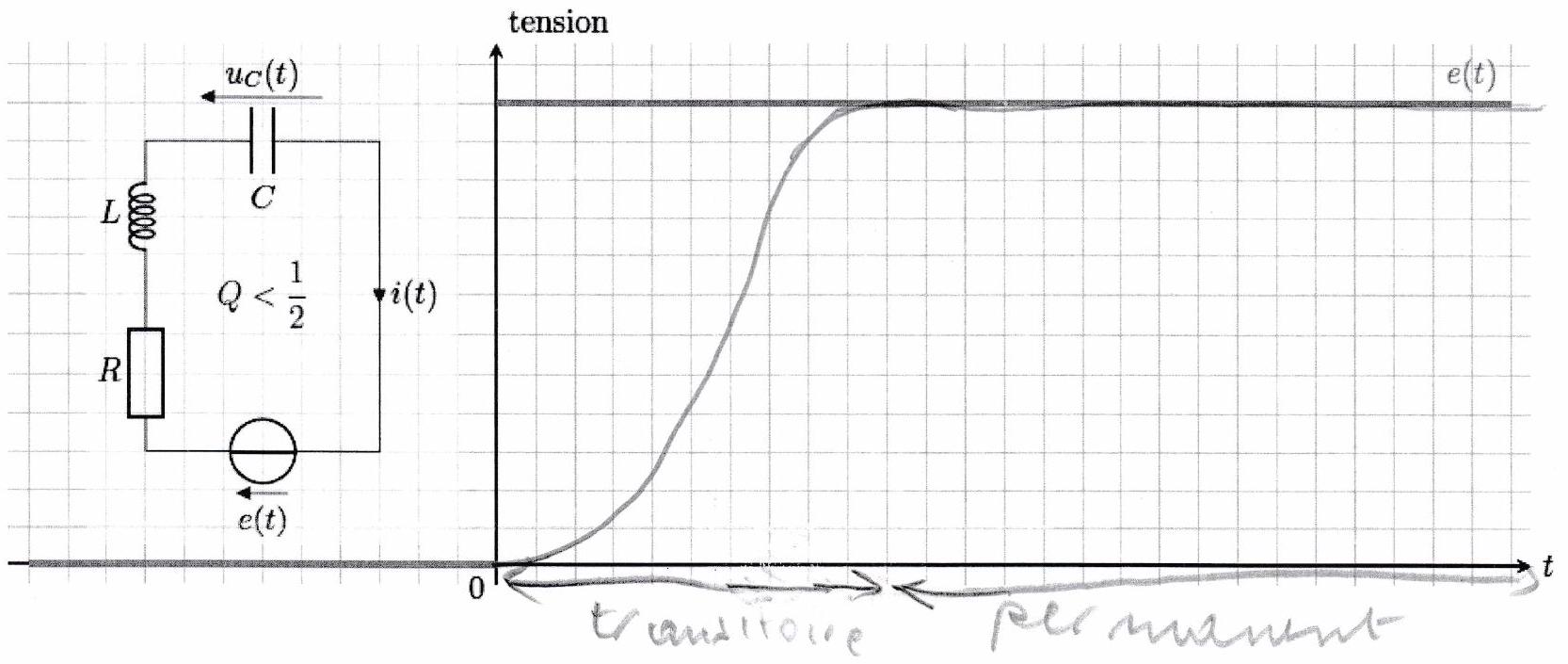
avec et deux constantes réelles qui dépendent des conditions initiales. Le régime transitoire est apériodique si l’oscillateur est soumis à un amortissement fort : il possède un facteur de qualité faible et le régime transitoire ne présente pas d’oscillations. La durée du régime transitoire dépend alors du terme le plus lent de la solution, c’est-à-dire celui associé à l’exponentielle dont le temps caractéristique est le plus grand.
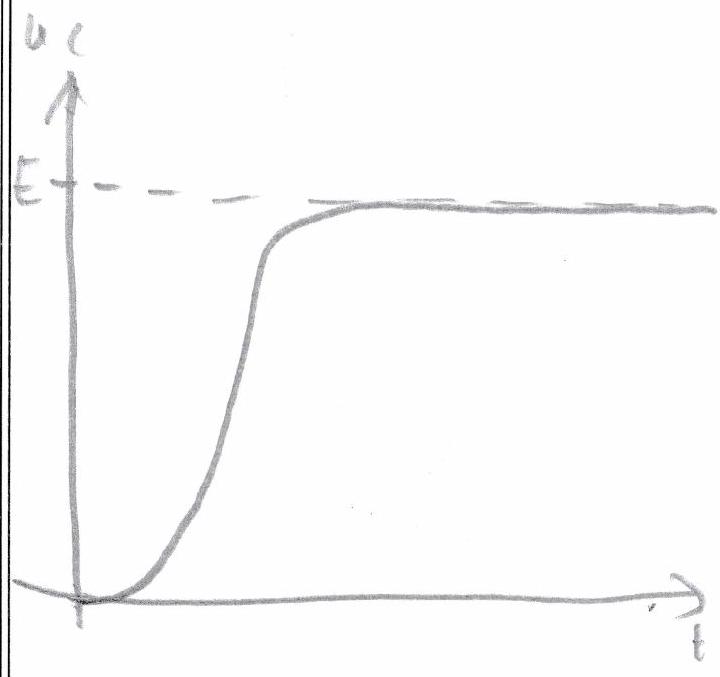
La durée du régime transitoire apériodique est de l’ordre de . “De loin”, le régime transitoire apériodique ressemble au régime transitoire d’un circuit du premier ordre. La condition initiale sur la dérivée de la grandeur représentée impose toutefois une évolution différente, notamment au début du régime transitoire. Cette distinction doit apparaître sur les représentations graphiques. On fera pour cela systématiquement apparaître la tangente à l’origine.
B) Régime transitoire critique
Si le discriminant est nul, c’est-à-dire si , le polynôme caractéristique admet une racine double réelle et négative
Si , le régime transitoire est critique. La solution générale de l’équation homogène est alors de la forme
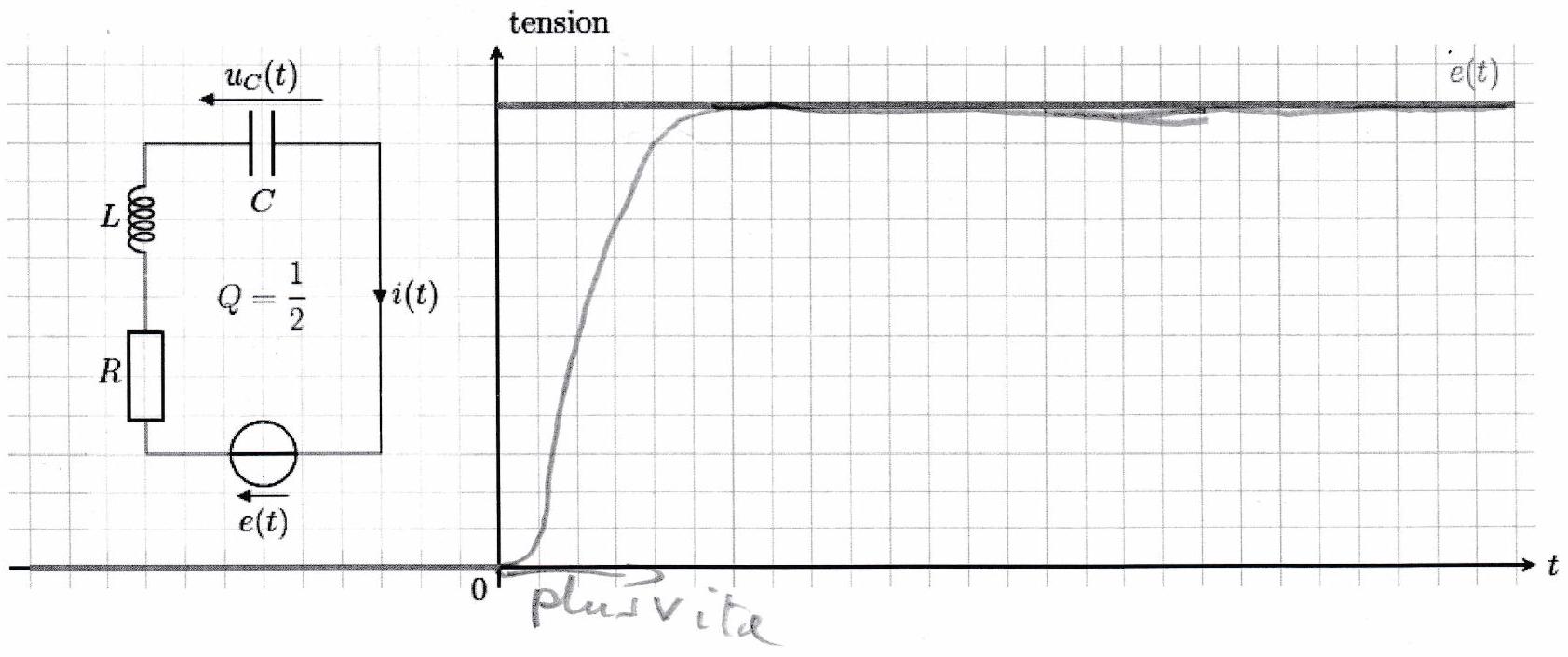
avec et deux constantes réelles qui dépendent des conditions initiales. Le régime critique correspond à un cas limite, pour lequel le régime transitoire est le plus court. De plus, il ne présente pas d’oscillation : le régime permanent est atteint sans dépassement.
La durée du régime transitoire critique est de l’ordre de . Là encore, malgré la ressemblance avec un régime transitoire du premier ordre, les conditions initiales doivent apparaître graphiquement.
C ) Régime transitoire pseudo-périodique¶
Si le discriminant est strictement négatif, c’est-à-dire si , le polynôme caractéristique admet deux racines complexes conjuguées
Si , le régime transitoire est pseudo-périodique. La solution générale de l’équation homogène est alors de la forme
avec et ou et deux constantes qui dépendent des conditions initiales. correspond à la pseudo-pulsation des oscillations.
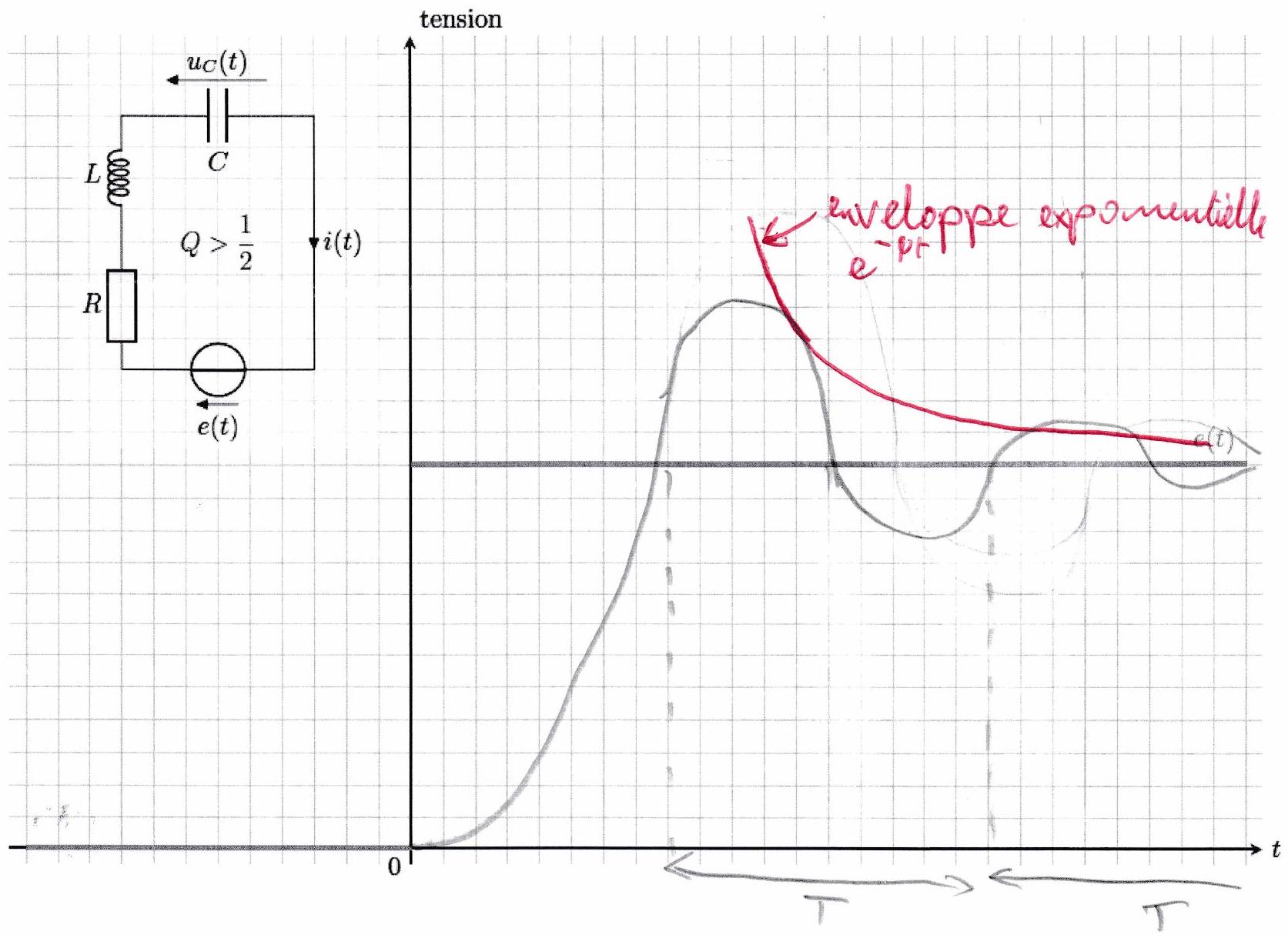
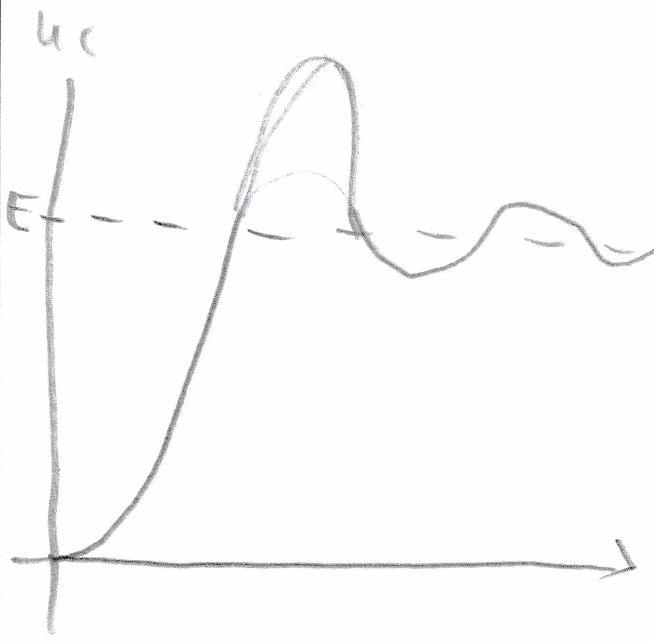
Le régime transitoire est pseudo-périodique si l’oscillateur est soumis à un amortissement faible : il possède un facteur de qualité élevé et le régime transitoire présente des oscillations. La durée du régime transitoire est donnée par l’enveloppe exponentielle des oscillations en .
La durée du régime transitoire pseudo-périodique est de l’ordre de . La pseudo-pulsation des oscillations du régime transitoire est différente de la pulsation propre. Seulement dans le cas d’un oscillateur faiblement amorti, c’est-à-dire si , on a . En pratique, dès que dépasse quelques unités, on pourra considérer .
Pendant le régime transitoire, la pseudo-pulsation, donc la pseudo-période, est constante. Seule l’amplitude des oscillations décroît !
Remarque¶
Durant le régime transitoire, le nombre d’oscillations visibles est de l’ordre de . Cela permet d’évaluer rapidement le facteur de qualité et de savoir si la période propre peut raisonnablement être approximée par la pseudo-période.
Application 1¶
On reprend le circuit de l’exercice de cours 1 et on donne et .
Exprimer et calculer la valeur de la résistance critique correspondant au régime critique ( ).
Donner la condition sur pour laquelle le régime transitoire présente des oscillations.
D) Résolution d’une équation différentielle du second degré¶
Pour résoudre une EDL2, on applique toujours la même méthode :
Écrire la solution générale de l’équation homogène (cf. ;
Trouver une solution particulière (constante si le second membre l’est) ;
Exprimer la solution générale de l’équation avec second membre ;
Déterminer les constantes d’intégration en exploitant les conditions initiales. Les coefficients et (ou et ) s’obtiennent en utilisant les conditions initiales avec la continuité des intensité parcourant la bobine et tension aux bornes du condensateur ;
Conclure en donnant la solution de l’équation qui satisfait les conditions initiales.
Remarque¶
L’ordre des étapes importe ! La détermination des constantes d’intégration doit toujours se faire après avoir trouvé la solution générale de l’équation différentielle avec second membre.
Application 2¶
On reprend la situation de l’exercice de cours 1 avec les valeurs de l’application 1 .
Donner, en les justifiant, les deux conditions initiales portant sur et sa dérivée première.
Donner l’expression de dans le cas où .
En déduire l’expression de .
Représenter graphiquement .
Faire de même pour .
IV ) Bilan énergétique¶
Le bilan énergétique s’effectue en multipliant la loi des mailles par :
Or :
On a donc :
où est la puissance fournie par le générateur ; est l’énergie stockée par le condensateur ; est l’énergie emmagasinée par la bobine ; est la puissance dissipée par effet Joule par la résistance.
L’énergie fournie par le générateur est en partie stockée dans le condensateur et dans la bobine et pour le reste dissipée par effet Joule.
V ) Analogie entre un circuit et un oscillateur mécanique¶
Il existe de nombreux systèmes décrits par des équations différentielles du deuxième ordre comme le circuit RLC. Ces systèmes sont nommés systèmes du deuxième ordre.
C’est le cas par exemple de l’oscillateur harmonique {masse ressort} vu au chapitre précédent auquel on rajouterait une force de frottement fluide , où est une constante positive et la vitesse, en plus de la force de rappel exercée par le ressort. Le tableau ci-contre précise la correspondance entre grandeurs analogues pour le circuit série et l’oscillateur mécanique.
| Donnée étudiée | circuit série | oscillateur mécanique |
|---|---|---|
| signal | ||
| signal dérivé | ||
| paramètres | C | |
| L | ||
| pulsation propre | ||
| facteur de qualité | ||
| énergie électrique/potentielle | ||
| énergie magnétique/cinétique |
VI ) Tableau récapitulatif¶
| Facteur de qualité | |||
|---|---|---|---|
| Régime | apériodique | critique | pseudo-périodique |
| Racines du polynôme caractéristique | |||
| Solution de l’équation homogène |
| |
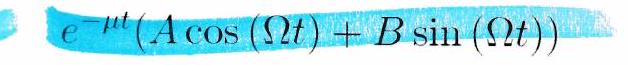
| | Durée du régime transitoire | quelques | quelques | quelques | | Évolution temporelle (réponse à un échelon) |
| |
|