Chapitre 2¶

Formation des images¶

I ) Vocabulaire¶

A ) Système optique¶

Définition 1 : Système optique¶

Un système optique ( $S$ ) est un ensemble de dioptres susceptibles de modifier la trajectoire des rayons lumineux ou les propriétés de la lumière.

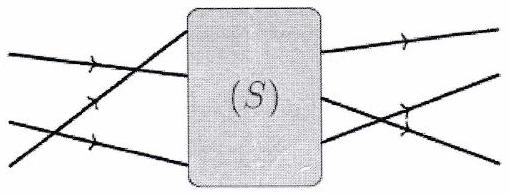
Définition 2 : Système optique centré¶

On dit qu’un système optique est centré si les éléments qui le constituent ont un axe de symétrie en commun appelé axe optique.

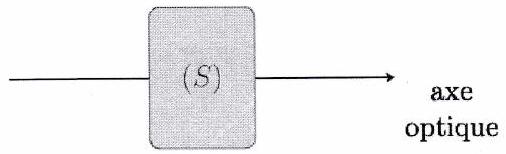
Exemple¶

L’objectif d’un appareil photo, une lunette astronomique, un microscope, . . .

B ) Objet et image¶

Définition 3 : Objet¶

Un objet est un ensemble de points qui émettent de la lumière. On dit de l’objet qu’il est :

• réel s’il est situé avant le système optique;

• virtuel sinon.

Exemple¶

Une étoile, une lampe, un arbre éclairé, . . .

Définition 4 : Image¶

Une image est une région de l’espace où convergent les rayons lumineux issus de l’objet après être passés à travers le système optique. On dit de l’image qu’elle est :

• réelle si elle se forme après le système optique, c’est-à-dire s’il est possible de la projeter sur un écran;

• virtuelle sinon.

Définition 5 : Objet et image à l’infini¶

• Un point objet (resp. image) est dit à l’infini SUR l’axe optique lorsque les rayons arrivent (resp. émergent) sur le système optique parallèlement entre eux et parallèlement à l’axe optique.

• Un point objet (resp. image) est dit à l’infini HORS l’axe optique lorsque les rayons arrivent (resp. émergent) sur le système optique parallèlement entre eux et inclinés par rapport à l’axe optique.

II ) Miroir plan¶

Définition 6 : Miroir plan¶

Un miroir plan est une surface plane réfléchissante (symbole ci-contre). Le système optique constitué d’un miroir plan possède un axe de révolution, qui est orthogonal au miroir : toute rotation autour de cet axe laisse inchangée la marche des rayons. Cet axe est l’axe optique du système $(\Delta)$.

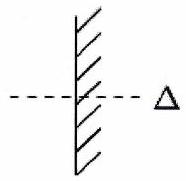
A ) Image par un miroir plan¶

Règles de tracés¶

• Les rayons doivent être tracés à la règle, et chaque rayon avec un stylo (ou feutre fin) de couleur différente.

• Les rayons doivent être orientés par une flèche.

• Les rayons incidents et les rayons émergents sont tracés en traits pleins, avec une flèche dessus.

• Les prolongements des rayons incidents et les prolongements des rayons émergents sont tracés en traits pointillés (rayons fictifs).

Exercice de cours à connaître 1¶

Construction de l’image par un miroir plan¶

1. Tracer la marche de trois rayons issus de $A$ et frappant le miroir $(\mathcal{M})$ en trois points différents.

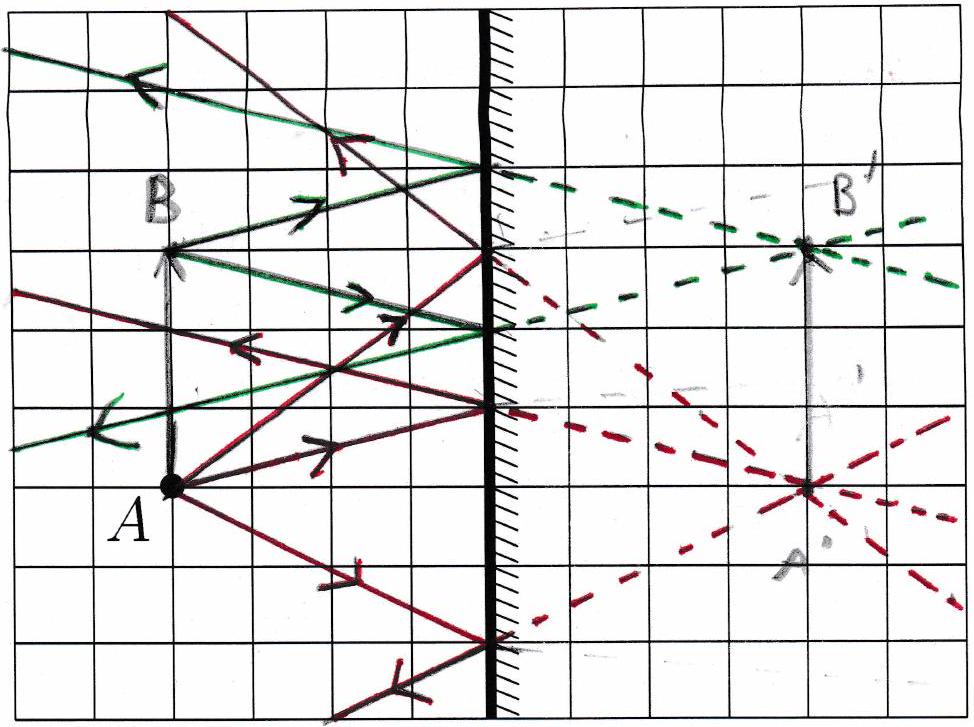
2. Tracer le prolongement en pointillés (ces rayons n’existent pas) des rayons réfléchis dans la partie arrière de $(\mathcal{M})$. Pour un observateur situé du côté de $A$, d’où semblent provenir les rayons réfléchis?

Considérons un objet $A B$ réel perpendiculaire à l’axe optique du miroir. 3. Tracer l’image $A^{\prime} B^{\prime}$ de cet objet par le miroir. 4. Comment est-elle par rapport à l’objet?

Image par un miroir plan¶

Un miroir plan donne de tout objet une image symétrique par rapport au plan du miroir.

B ) Stigmatisme rigoureux et aplanétisme¶

Définition 7 : Stigmatisme¶

Un système optique est dit rigoureusement stigmatique s’il donne d’un objet ponctuel $A$ un point image $A^{\prime}$ unique. On dit que $A^{\prime}$ est l’image de $A$ ou que $A$ et $A^{\prime}$ sont conjugués par le système optique. Dans ce cas, il existe une relation entre la position de l’image et celle de l’objet appelée formule de conjugaison.

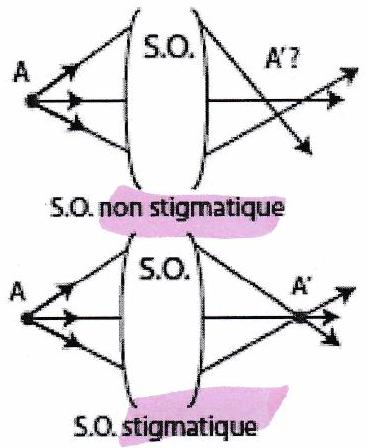
Définition 8 : Aplanétisme¶

On dit qu’un système optique aplanétique sì si l’image d’un objet perpendiculaire à l’axe optique l’est aussi.

Le stigmatisme rigoureux est-il nécessaire pour avoir une image nette? Autrement dit, à quelle condition verra-t-on un point et non une tache? Qu’il s’agisse de la rétine de l’œil ou d’un capteur d’appareil photo numérique, les capteurs sont constitués de cellules: les cônes/bâtonnets sur la rétine et les pixels pour l’appareil photo. Cela confère au capteur une résolution maximale : le récepteur ne peut pas distinguer des détails plus petits que le plus petit élément qui le constitue. Des rayons émergeant du système optique parvenant sur la même cellule photosensible du capteur peuvent être considérés comme confondus. L’observateur aura done l’impression de voir un point.

Illustration avec un capteur numérique : $5 \times 5$ pixels

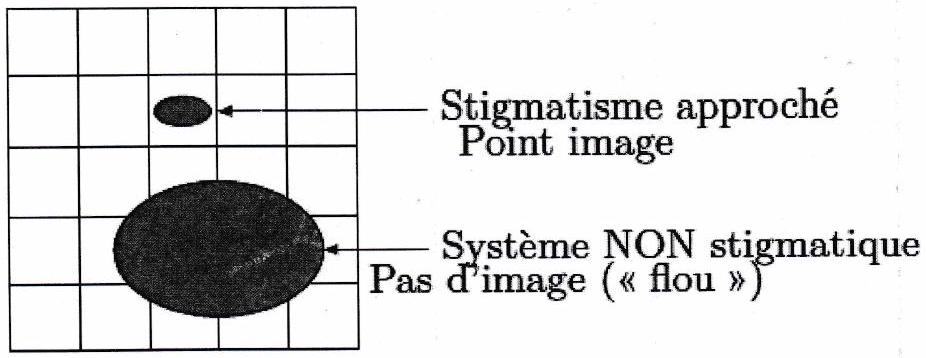
Stigmatisme approché¶

Un système optique réalise un stigmatisme approché si les rayons incidents issus d’un point objet $A$ passent au voisinage de $A^{\prime}$ de dimension inférieure à la dimension caractéristique des cellules du capteur. Cette notion dépend donc du capteur utilisé.

Remarque¶

On regroupe les causes de non stigmatisme en deux catégories principales :

• Les aberrations géométriques : on considère une lumière monochromatique. L’image d’un point n’est alors pas exactement un point.

• Les aberrations chromatiques : la lumière blanche est composée de plusieurs longueurs d’onde $\lambda$. Or l’indice optique $n$ du verre de la lentille dépend de $\lambda$ (phénomène de dispersion), donc les différentes onde lumineuses monochromatiques ne vont pas converger exactement au même point. Il en résulte des taches colorées.

B ) Conditions de Gauss¶

Un système optique usuel (excepté le miroir plan ) n’est pas rigoureusement stigmatique pour tout point, il ne peut donc pas présenter d’aplanétisme rigoureux. Malgré tout, on peut obtenir des images de bonne qualité au moyen d’un système optique en se plaçant dans les conditions de GAUSS, le système est alors approximativement stigmatique et aplanétique.

Conditions de Gauss¶

Le système optique est utilisé dans les conditions de Gauss si :

• les rayons sont peu inclinés par rapport à l’axe optique;

• les rayons sont peu éloignés de l’axe optique.

On parle de rayons paraxiaux.

Remarque¶

Dans les conditions de Gauss, les angles $\theta$ entre l’axe optique et les rayons lumineux seront très petits devant 1 radian, et on pourra alors écrire, avec $\theta$ en radian : $\sin (\theta) \simeq \theta ; \tan (\theta) \simeq \theta ; \cos (\theta) \simeq 1$.

IV ) Lentilles minces¶

A) Différents types de lentilles¶

Définition 9 : Lentille¶

Une lentille est un matériau transparent, homogène et isotrope délimité par deux dioptres dont l’un au moins est sphérique. Une lentille est mince si son épaisseur e est très inférieure aux rayons de courbure ( $R_{1}$ et $R_{2}$ ) des deux dioptres. On note $\Delta$ l’axe optique : c’est l’axe de révolution de la lentille. C’est un système optique centré, que l’on supposera stigmatique et aplanétique (lorsqu’il est utilisé dans les conditions de Gauss). On distingue deux catégories de lentilles minces:

• les lentilles convergentes dont le centre est plus épais que les bords;

• les lentilles divergentes dont le centre est plus mince que les bords.

biconcave

Pour modéliser une lentille mince convergente ou divergente, on néglige complètement son épaisseur et on représente les lentilles par un trait. Les symboles des lentilles minces convergentes et divergentes sont les suivants :

• Lentilles convergentes

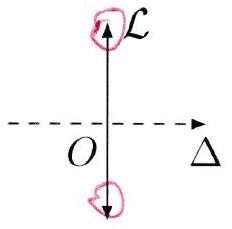
• Lentilles divergentes

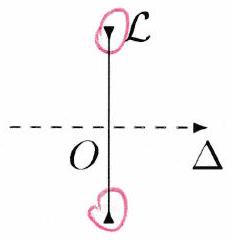
B ) Points particuliers¶

Définition 10 :¶

Une lentille possède trois points particuliers.

• le point $O$ : c’est le centre optique de la lentille. Tout rayon passant par le centre optique d’une lentille mince ressort sans être dévié;

• le point $F$ : c’est le foyer principal objet. Un objet ponctuel situé en ce point donnera une image à l’infini SUR l’axe optique;

• le point $F^{\prime}$ : c’est le foyer principal image. Un objet ponctuel situé à l’infini SUR l’axe optique donnera une image en ce point.

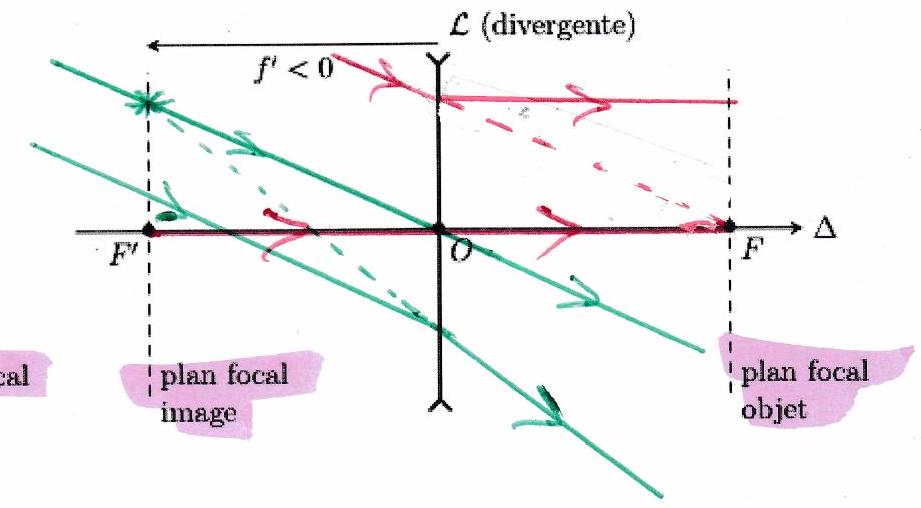
Définition 11 : Plan focal objet et image¶

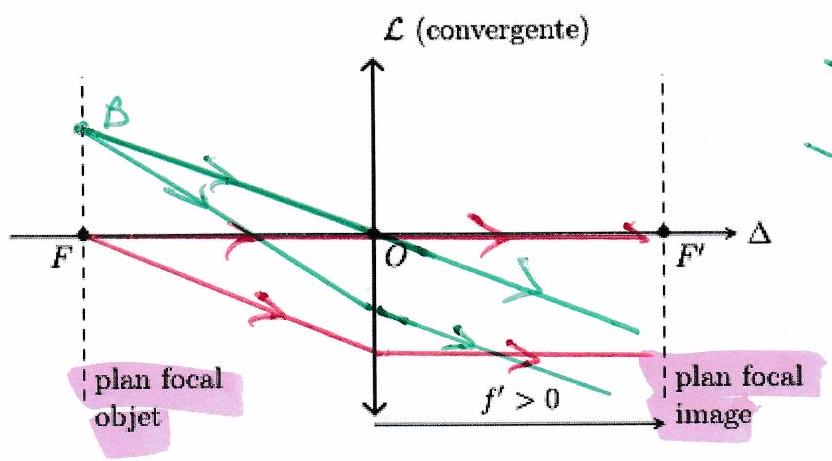
Le plan focal objet (resp. image) est le plan perpendiculaire à l’axe optique passant par le foyer principal objet (resp. image). Tout point qui appartient au plan focal objet (resp. image) est appelé foyer secondaire objet (resp. image).

Un objet ponctuel situé dans le plan focal objet (foyer secondaire objet) donnera une image à l’infini HORS l’axe optique. Un objet ponctuel situé à l’infini HORS l’axe optique donnera une image situé dans le plan focal image (foyer secondaire image).

C ) Distance focale et vergence¶

Définition 12 : Distance focale¶

Une lentille est caractérisée par sa distance focale $\overline{O F^{\prime}}$ que l’on notera $f^{\prime}$. C’est une distance algébrique :

• $\overline{O F^{\prime}}>0$ pour une lentille convergente;

• $\overline{O F^{\prime}}<0$ pour une lentille divergente.

On a toujours $\overline{O F}=-\overline{O F^{\prime}}$ : les foyers objet et image sont symétriques par rapport au centre optique.

Remarque¶

ATTENTION ERREUR A NE PAS COMMETTRE¶

$F$ et $F^{\prime}$ ne sont pas conjugués par la lentille mince : $F^{\prime}$ N’est PAS l’image de $F$ par la lentille mince.

Définition 13 : Vergence¶

La vergence $V$ d’une lentille, exprimée en dioptries $(\delta)$, est définie comme l’inverse de la distance focale :

Exemple¶

La correction nécessaire à un œil est exprimée en dioptries : c’est la vergence des verres/lentilles à porter.

Remarque¶

ATTENTION : Soyez très vigilants dans les notations $f, f^{\prime}, F, F^{\prime}$ : les foyers doivent être notés avec une lettre majuscule, et les distances focales avec une lettre minuscule.

D) Image par une lentille¶

Tracé d’une image¶

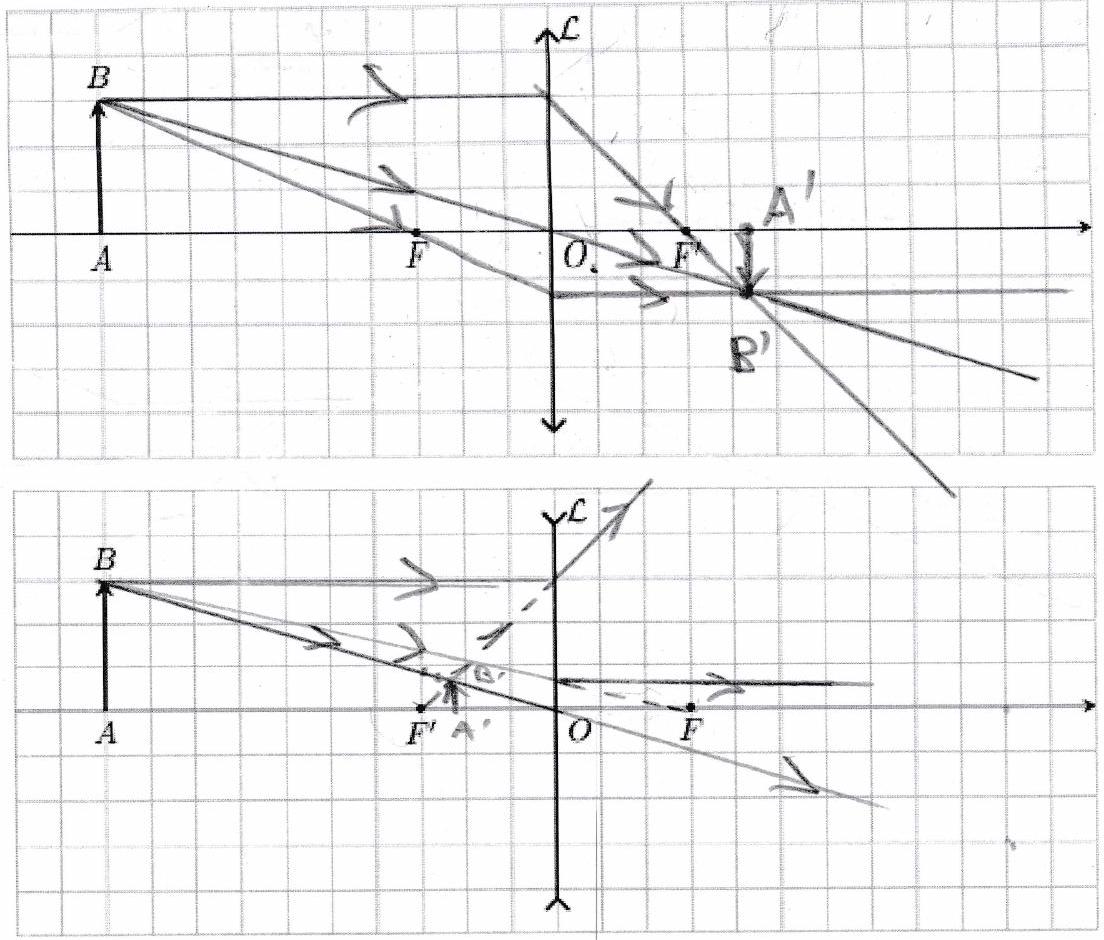
Pour représenter l’image $A^{\prime} B^{\prime}$ d’un objet $A B$ perpendiculaire à l’axe optique ( $\Delta$ ) avec $A$ sur ( $\Delta$ ) et $B$ hors de ( $\Delta$ ), il faut tracer les trois rayons suivants issus de $B$ afin de déterminer $B^{\prime}$ :

• un rayon passant par le centre optique n’est pas dévié;

• un rayon incident parallèle à l’axe optique ressort en passant par le foyer principal image;

• un rayon incident passant par le foyer principal objet ressort parallèle à l’axe optique. $B^{\prime}$ est à l’intersection de ces trois rayons, et on en déduit $A^{\prime}$ qui est le projeté orthogonal de $B^{\prime}$ sur ( $\Delta$ ).

Exemple¶

Application 1¶

Réaliser les tracés ci-dessous. Préciser pour chaque tracé la nature de l’objet (réel/virtuel) et la nature de l’image (réelle/virtuelle).

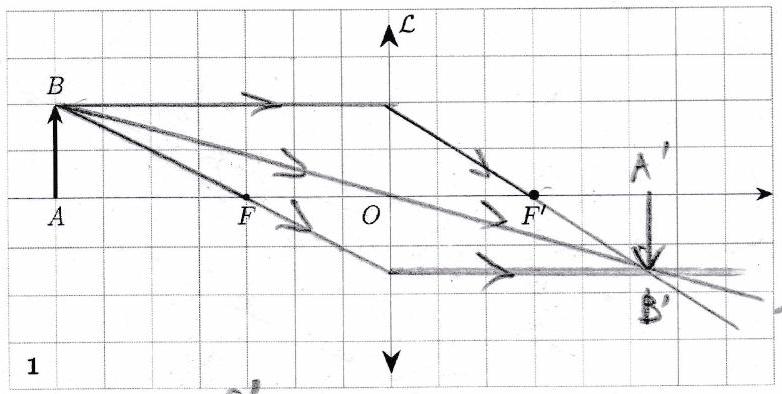
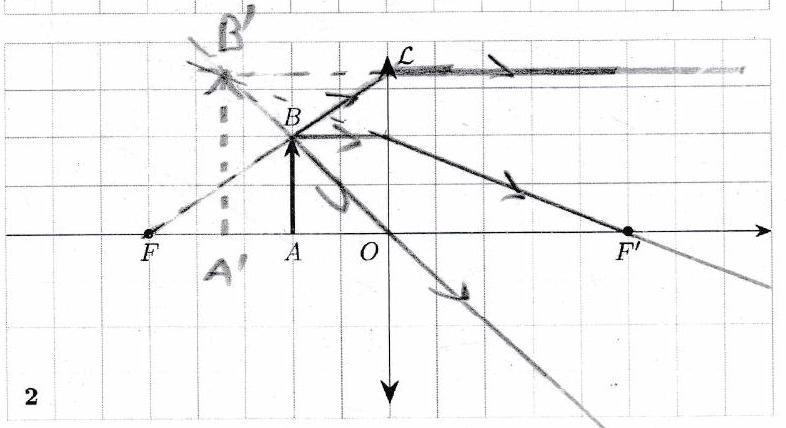
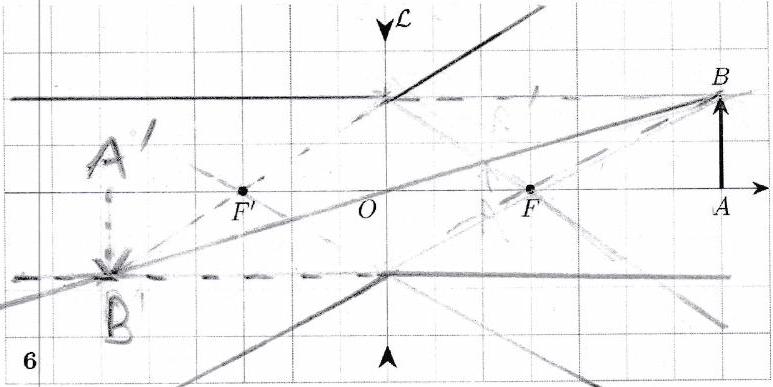
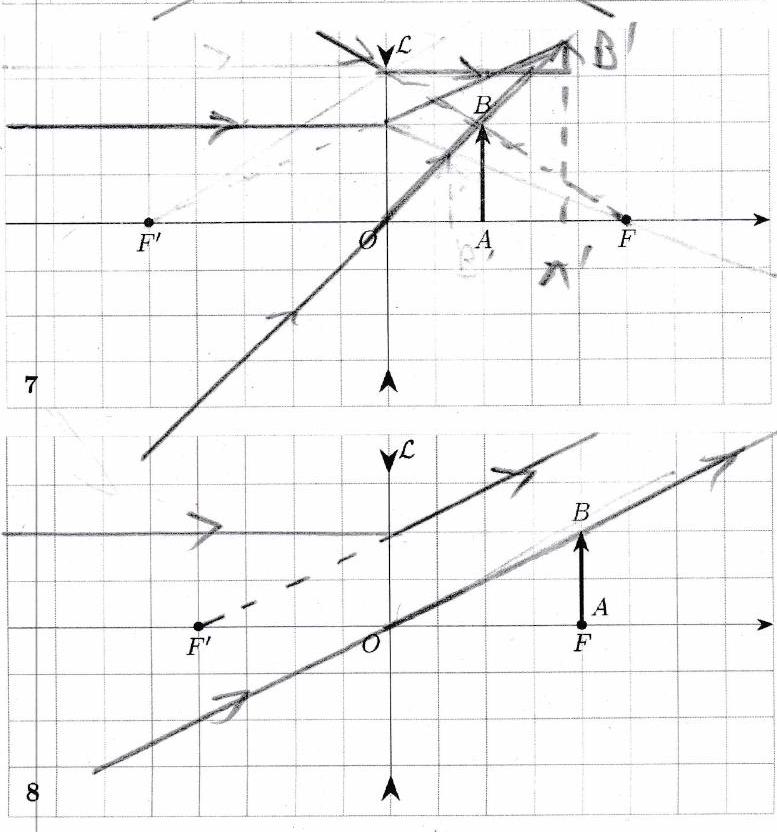
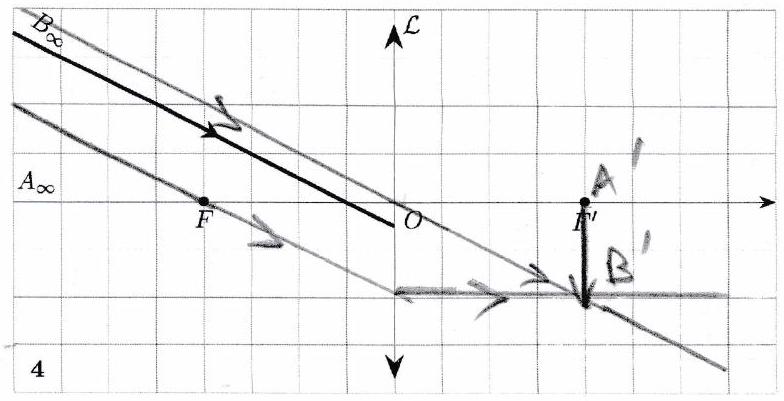
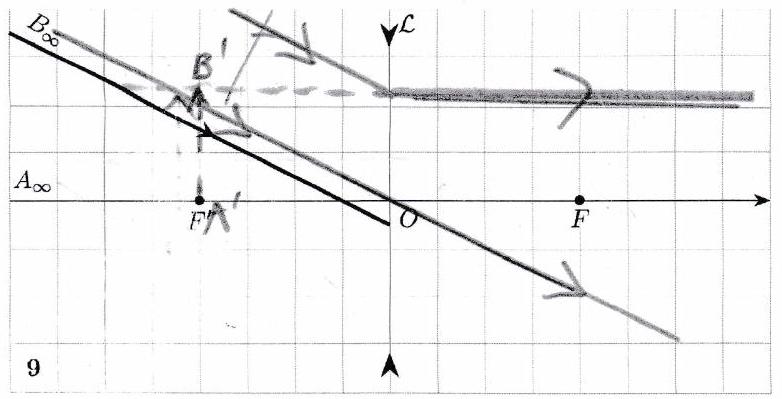
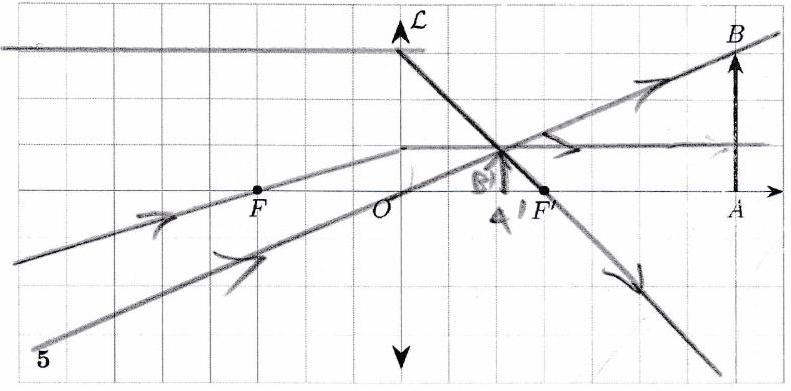
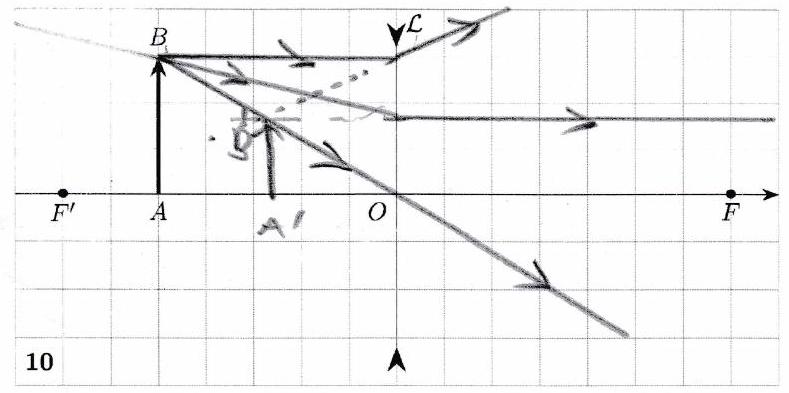
Pour obtenir une image réelle avec une lentille convergente, l’objet doit être placé avant le foyer objet.

Remarque¶

En pratique, seuls deux de ces rayons suffisent, le troisième peut éventuellement servir de confirmation.

Application 2¶

Représenter les rayons qui émergent de la lentille.

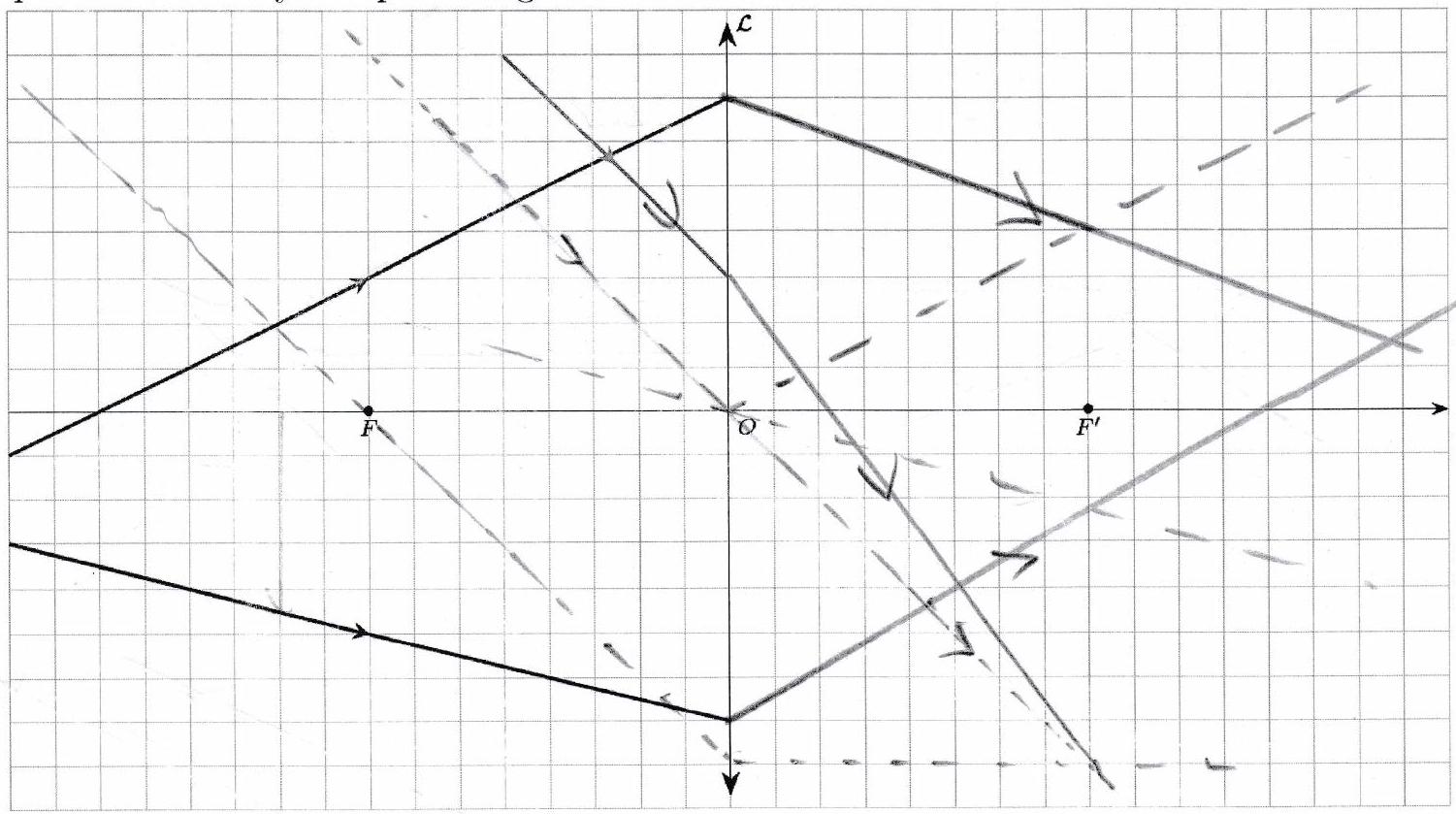
V ) Relations de conjugaison et de grandissement¶

A) Repérage¶

Définition 14 : Distances algébriques¶

En optique, on utilise les distances algébriques, notées avec une barre au-dessus $\overline{O A}$ qui renseignent sur la distance (au sens habituel) qui sépare les points $O$ et $A$, et sur le sens dans lequel est mesurée la distance. Pour cela, il est nécessaire de définir un sens positif :

• Le long de l’axe optique, le sens positif est le sens de la lumière incidente.

• Perpendiculairement à l’axe optique, le sens positif est souvent choisi «vers le haut ».

Rappel¶

Les angles sont orientés : ils peuvent être positifs ou négatifs. En général, on choisit le sens trigonométrique comme sens positif.

B ) Grandissement transversal¶

Définition 15 : Grandissement transversal¶

Le grandissement transversal est le rapport algébrique de la taille de l’image $\overline{A^{\prime} B^{\prime}}$ sur celle de l’objet $\overline{A B}$, celui-ci étant orthogonal à l’axe optique :

C’est une grandeur algébrique (positive ou négative) sans dimension.

Exercice de cours à connaître 2¶

1. Que peut-on dire sur l’objet et l’image si $\gamma>0$ ? si $\gamma<0$ ?

2. Que peut-on dire sur l’objet et l’image si $|\gamma|>1$ ? si $|\gamma|<1$ ?

Application 3¶

Reprendre l’Application 1 et préciser pour chaque tracé :

• image agrandie / image rétrécie / image de même taille / $\hat{h}|>1 /|\gamma|<1 /|\gamma|=1$

• image droite / image renversée $/ \gamma>0 / \gamma<0$

C) Relations¶

Les relations de conjugaison et de grandissement transversal sont valables aussi bien pour les lentilles convergentes que divergentes. Les relations de grandissement transversal relient la taille de l’image à celle de l’objet. Les relations de conjugaison sont des relations mathématiques qui relient la position d’un point objet situé sur l’axe optique à la position du point image conjugué. Soit $A^{\prime} B^{\prime}$ l’image de $A B$ par une lentille $\mathcal{L}$ de distance focale $f^{\prime}$ : on dit que $A^{\prime} B^{\prime}$ et $A B$ sont conjugués par $\mathcal{L}$.

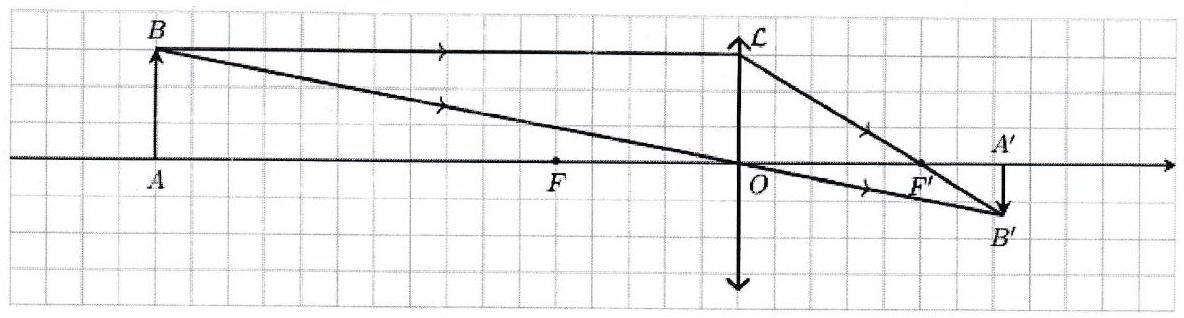
Relations de Descartes¶

Les relations de Descartes, ou relations avec origine au centre optique s’écrivent :

Relations de Newton¶

Les relations de Newton, ou relations avec origine aux foyers s’écrivent :

Remarque
ATTENTION ERREUR A NE PAS COMMETTRE¶

Toutes les grandeurs qui interviennent dans les relations de conjugaison sont des grandeurs algébriques. L’orientation choisie le long de l’axe optique est celle de la lumière incidente.

Ainsi, il faut traduire «on photographie un objet à une distance de $5 m>p \operatorname{par} \overline{O A}=-5 \mathrm{~m}$, si l’axe optique est orienté dans le sens de la lumière incidence.

Exercice de cours à connaître 3¶

En utilisant les relations de Descartes, montrer que pour obtenir une image réelle avec une lentille convergente, l’objet doit être placé avant le foyer objet.

Application 4¶

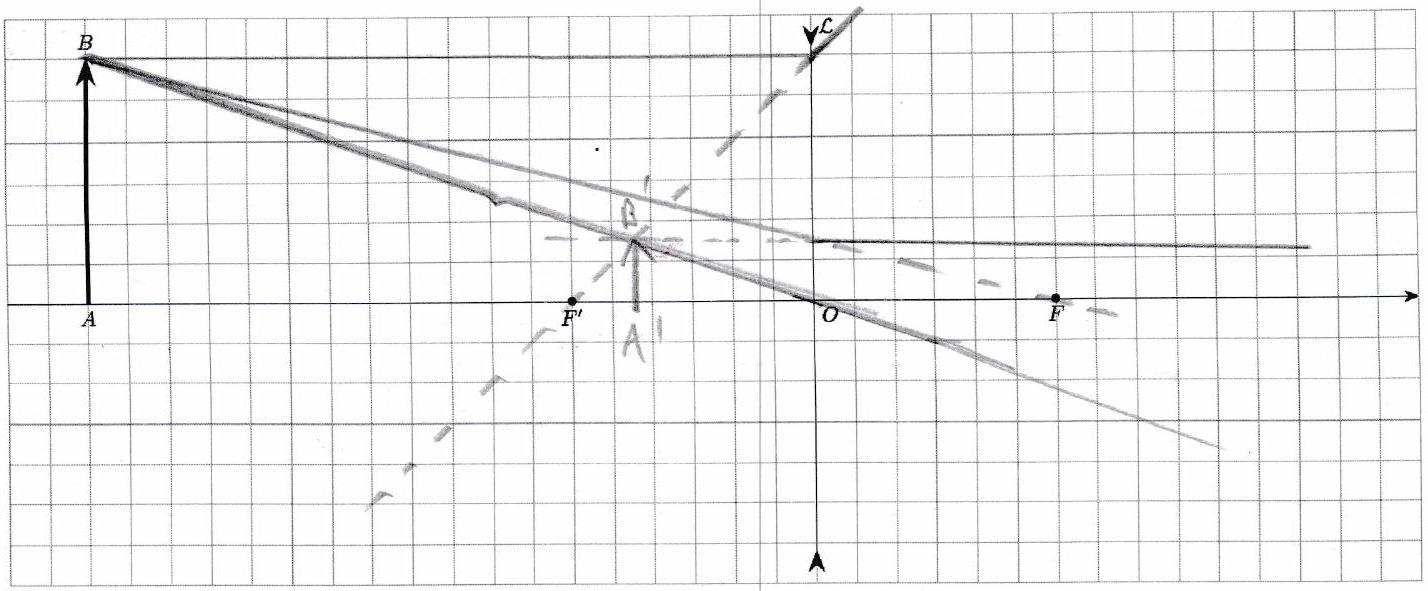
On s’intéresse à la formation de l’image $A^{\prime} B^{\prime}$ image d’un objet $A B$ formée par une lentille de distance focale $f^{\prime}=-3,0 \mathrm{~cm}$ dans la situation représentée ci-dessous.

1. Exprimer, puis calculer les position et taille de l’image avec les relations de Descartes.

2. Faire de même en utilisant les relations de Newton.

3. Retrouver ces résultats en construisant l’image $A^{\prime} B^{\prime}$ de $A B$.

D ) Projection de l’image réelle d’un objet réel¶

On cherche à projeter l’image d’un objet éclairé sur un écran, que l’on souhaite agrandie, lumineuse et nette sur l’écran. Les positions de l’objet et de l’écran sont considérées fixes et la distance entre les deux est notée $D$.

Exercice de cours à connaître 4¶

1. Lors d’une projection, quelles sont les natures (réelle/virtuelle) de l’objet et de l’image?

2. Quel type de lentille permet la réalisation d’une projection?

3. En suivant la méthode ci-dessous, montrer qu’une projection peut être réalisée que si la distance $D$ séparant l’objet et l’écran est supérieure à une certaine distance dépendant de la distance focale $f^{\prime}$. (a) Faire un schéma de la situation et poser $D=\overline{A A^{\prime}}$. (b) Appliquer la relation de conjugaison de Descartes. (c) Exprimer $\overline{O A^{\prime}}$ en fonction de $\overline{O A}$ et $D$. (d) Utiliser les deux équations obtenues précédemment pou trouver une équation du deuxième degré vérifiée par $\overline{O A}$. (e) En exploitant le fait que le discriminant de l’équation précédente doit être positif pour obtenir des solutions réelles (donc ayant un sens physique), obtenir la condition reliant $D$ et $f^{\prime}$ pour réaliser une projection.

Condition sur la distance objet-écran pour la projection¶

Pour réaliser la projection d’un objet sur un écran à l’aide d’une lentille convergente de distance focale $f^{\prime}$, il faut placer l’écran à une distance $D$ de l’objet quatre fois supérieure à la distance focale :

Remarque¶

ATTENTION ERREUR A NE PAS COMMETTRE¶

Cette relation ne fait que donner la distance minimale qui doit séparer un objet d’un écran pour pouvoir réaliser la projection de l’objet sur l’écran avec une lentille convergente donnée, elle ne sert à rien d’autre!

VI ) Exemples de systèmes optiques¶

A ) L’œil

1 ) Modélisation¶

L’œil humain a sensiblement la forme d’une sphère. Il est divisé en deux parties séparées par le cristallin, assimilé à une lentille mince biconvexe, convergente. Le cristallin est déformable : sa distance focale peut être modifiée pour former des images nettes d’objets situés à différentes distances sur la rétine située à une distance fixe du cristallin. On dit que l’œil accommode.

L’iris joue le rôle d’un diaphragme et définit la pupille. Il permet de réguler la quantité de lumière qui arrive au

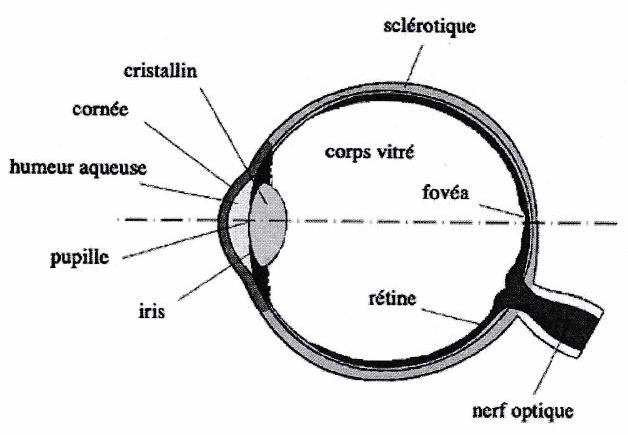
niveau de la rétine.

La rétine sert de détecteur. Elle est recouverte de cellules photosensibles, les cônes et les bâtonnets, qui transforment l’excitation lumineuse en influx nerveux. La distance entre la rétine et le cristallin est invariable : $d=17 \mathrm{~mm}$.

Modèle de l’œil¶

L’œil peut être modélisé par l’association :

• d’un diaphragme : l’iris;

• d’une lentille mince convergente de distance focale variable: le cristallin;

• d’un capteur plan fixe (un écran par exemple) : la rétine.

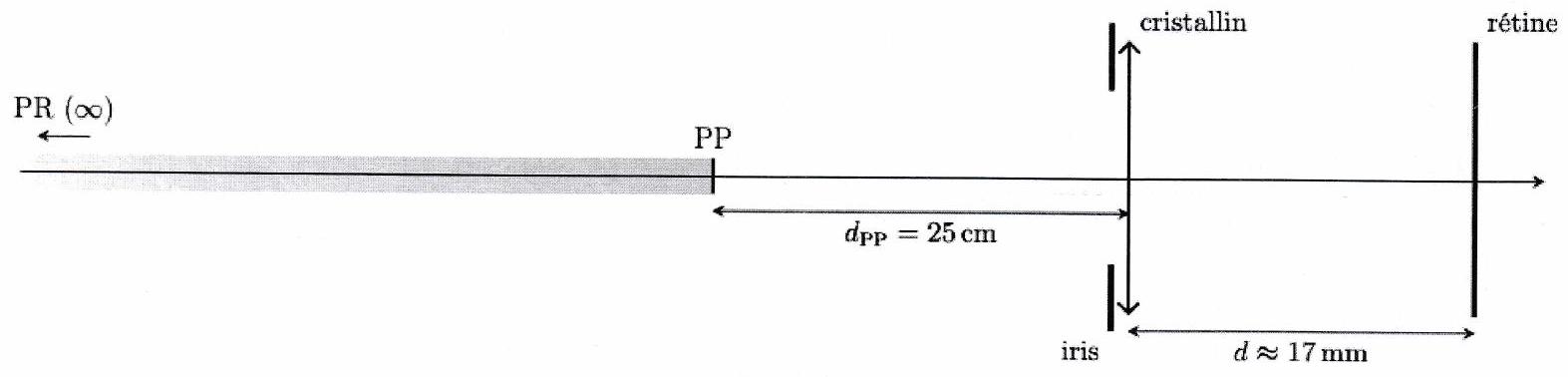
2 ) Plage d’accommodation¶

L’œil ne peut voir un objet net que si son image se forme sur la rétine.

Définition 16 : Punctum Remotum (PR)¶

Le punctum remotum ( PR ) est le point le plus éloigné dont l’œil est capable de produire une image nette. Pour un l’œil emmétrope (sain), il se situe à l’infini : $d_{\mathrm{PR}}=\infty$. Pour observer un objet au PR, l’œil n’accommode pas.

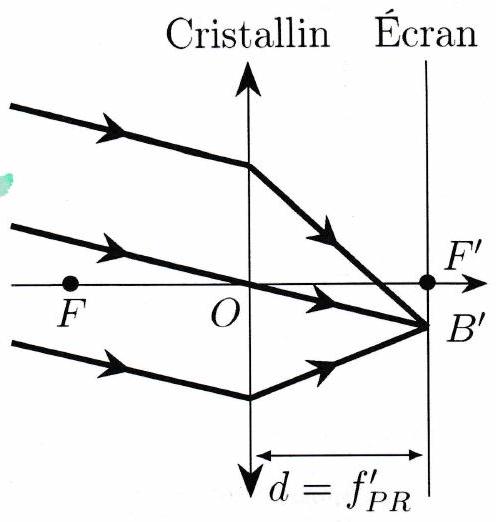
Pour observer un objet au PR, l’œil ne se fatigue donc pas : la plupart des instruments optiques destinés à une observation humaine (microscope, lunette astronomique, etc.) forment une image à l’infini pour que leur utilisation soit confortable.

Pour voir des objets plus proches, l’œil doit accommoder : le cristallin se bombe, grâce aux muscles ciliaires, afin de diminuer sa distance focale (il augmente sa vergence). Le plan de mise au point s’avance.

Définition 17 : Punctum Proximum (PP)¶

Le punctum proximum ( PP ) est le point le plus proche dont l’œil est capable de produire une image nette. Pour un œil emmétrope, on retiendra : $d_{\mathrm{PP}}=25 \mathrm{~cm}$. Le PP et le PR définissent la plage d’accommodation : c’est la plage de vision nette.

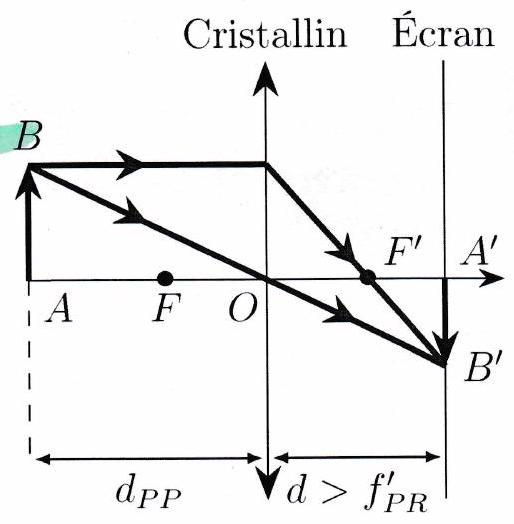
Exercice de cours à connaître 5¶

1. Faire un schéma rendant compte de la vision d’un objet situé au punctum remotum d’un œil emmétrope.

2. Pour que l’objet soit toujours vu net, où doit se former l’image de l’objet par le cristallin? Dans l’œil, qu’est-ce qui ne varie pas? Qu’est-ce qui varie pour permettre la vision nette?

3. Faire un schéma rendant compte de la vision d’un objet situé entre le punctum remotum et le punctum proximum. Comment évolue la distance focale du cristallin?

3 ) Limite de résolution angulaire¶

Deux points objet $A$ et $B$ sont vus distinctement si $A^{\prime}$ et $B^{\prime}$, leurs images par le cristallin se forment sur deux cellules de la rétine différentes. Pour cela, il faut que $A^{\prime} B^{\prime}$ soit supérieur à la taille d’une cellule de la rétine. Ainsi, il faut que l’angle entre les rayons arrivant dans l’œil soit suffisamment grand (la taille de l’œil étant fixée).

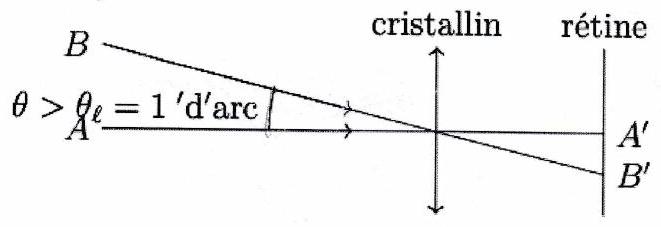
Définition 18 : Limite de résolution angulaire¶

La limite de résolution angulaire est le plus petit angle $\varepsilon$ sous lequel deux points peuvent être résolus (= distingués). Pour l’œil humain, cette limite est de l’ordre de 1’ dans de bonnes conditions d’éclairement (ni trop sombre, ni trop lumineux).

Application 5¶

Déterminer la hauteur $h$ du plus petit objet que l’œil peut distinguer à une distance $d$ de $25 \mathrm{~cm}, 5 \mathrm{~m}$ et 100 m . Quel paramètre permet de caractériser la taille apparente d’un objet?

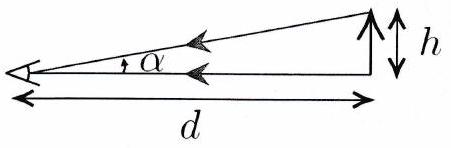
Définition 19 : Taille apparente¶

La taille apparente, ou taille angulaire ou diamètre apparent ou diamètre angulaire d’un objet correspond à l’angle sous lequel est vu un objet.

B ) L’appareil photographique¶

1 ) Modélisation¶

Un appareil photo est constitué :

• d’un objectif (association de plusieurs lentilles, miroirs et diaphragmes), modélisé par une lentille convergente de distance focale $f^{\prime}$ (appelée aussi focale) associée à un diaphragme de diamètre $D$ réglable placé avant la lentille;

• d’un capteur CCD qui enregistre l’image, modélisé par un écran à une distance $d$ réglable derrière la lentille. Le capteur CCD est une matrice de cellules photosensibles : les pixels. Il est caractérisé par la taille des pixels, le grain noté $g$ (en référence aux anciens appareils argentiques) et sa dimension $L \times l$ en pixels.

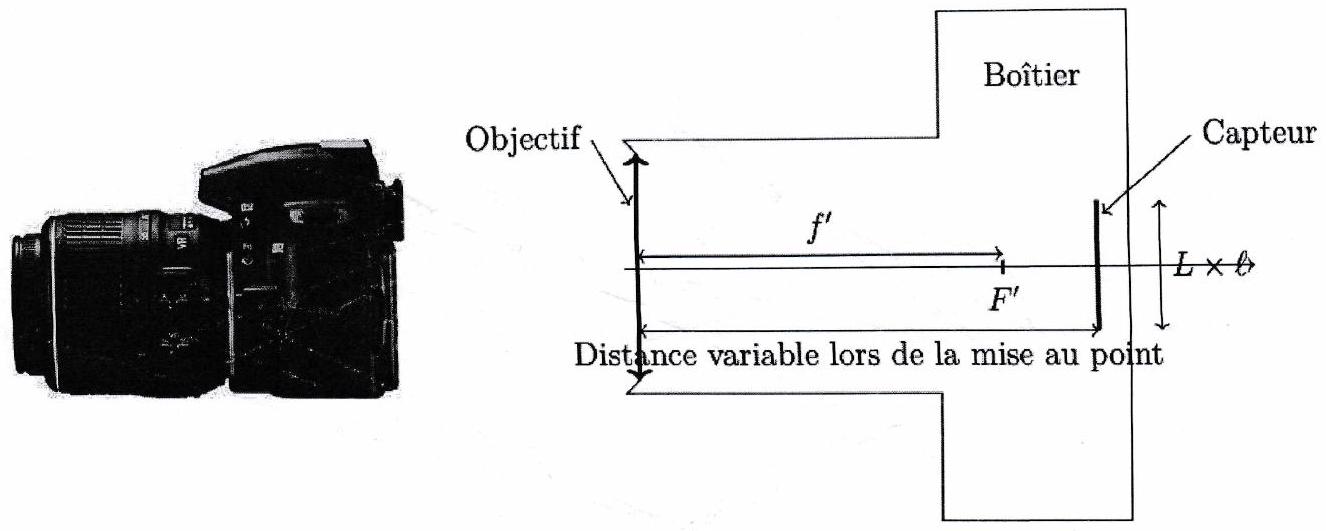
C ) Mise au point¶

Pour obtenir une image nette, il faut que l’image du sujet photographié se forme sur le capteur. Lorsqu’on fait la mise au point à l’infini (pour former une image nette d’un sujet très éloigné), la distance $d$ est égale à la focale de l’appareil. Quand on souhaite obtenir une image d’un sujet plus proche, il faut augmenter la distance $d\left(d>f^{\prime}\right)$.

D ) Profondeur de champ¶

Le capteur n’est pas ponctuel, mais est constitué de pixels ayant une certaine extension spatiale (le grain $g$ ). Tant que l’image d’un point objet sur le capteur sera d’une taille inférieure au grain, si l’exposition est suffisante, tout se passera comme si l’image était ponctuelle, ce qui donnera une image nette.

Définition 20 : Profondeur de champ¶

On appelle alors profondeur de champ l’étendue de la zone de netteté obtenue sur la photographie. Il s’agit alors de la distance entre les premiers et les derniers éléments nets de l’image.

Exercice de cours à connaître 6¶

On souhaite déterminer graphiquement la profondeur de champ dans le cas où l’appareil photo est réglé pour photographier nettement le point $A$. On considère un capteur placé dans le plan de $A^{\prime}$, et un pixel de hauteur $g$ centré sur l’axe optique.

1. Déterminer la position du point objet $A$ conjugué du point image $A^{\prime}$ situé sur la cellule du capteur et l’axe optique.

2. Déterminer les positions des deux points image extrêmes, $A_{1}^{\prime}$ et $A_{2}^{\prime}$ qui apparaîtront nets sur l’écran.

3. Déterminer les positions des deux points objets $A_{1}$ et $A_{2}$ conjugués par la lentille avec $A_{1}^{\prime}$ et $A_{2}^{\prime}$.

4. Identifier la profondeur de champ.

E ) Système optique composé¶

Quand un système comporte plusieurs éléments, on construit l’image intermédiaire $A_{1} B_{1}$ formée par le premier élément, qui devient l’objet du deuxième, et ainsi de suite :

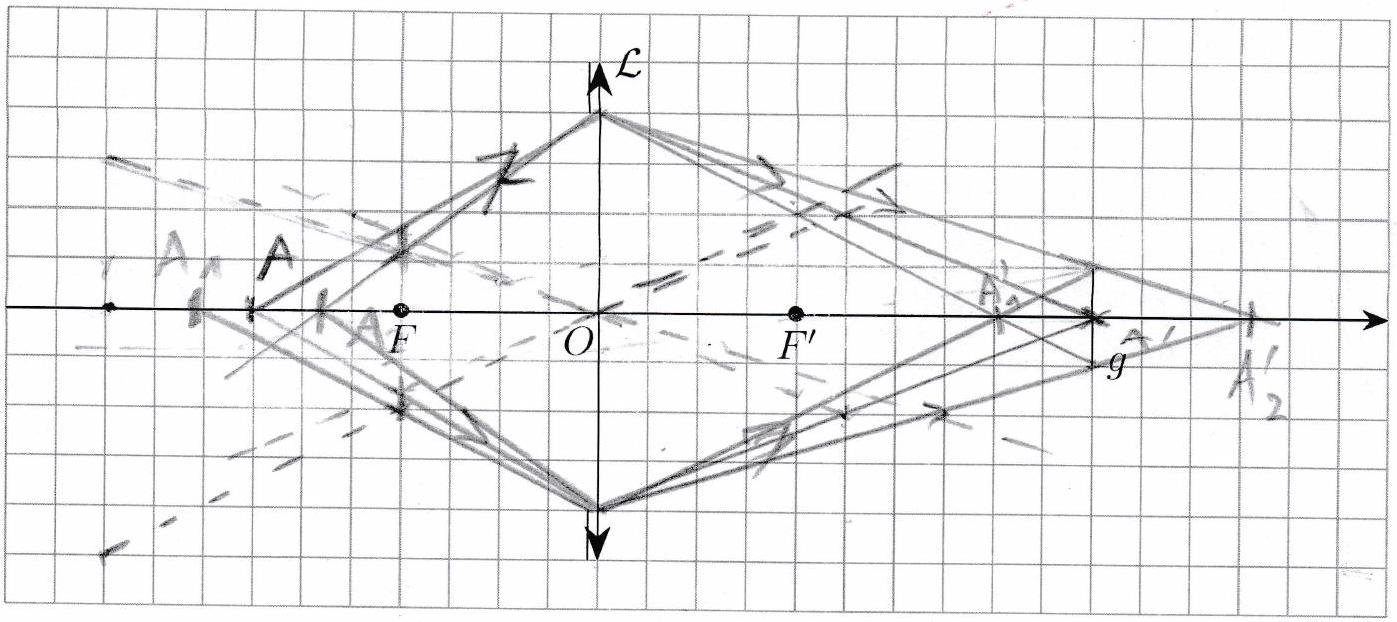
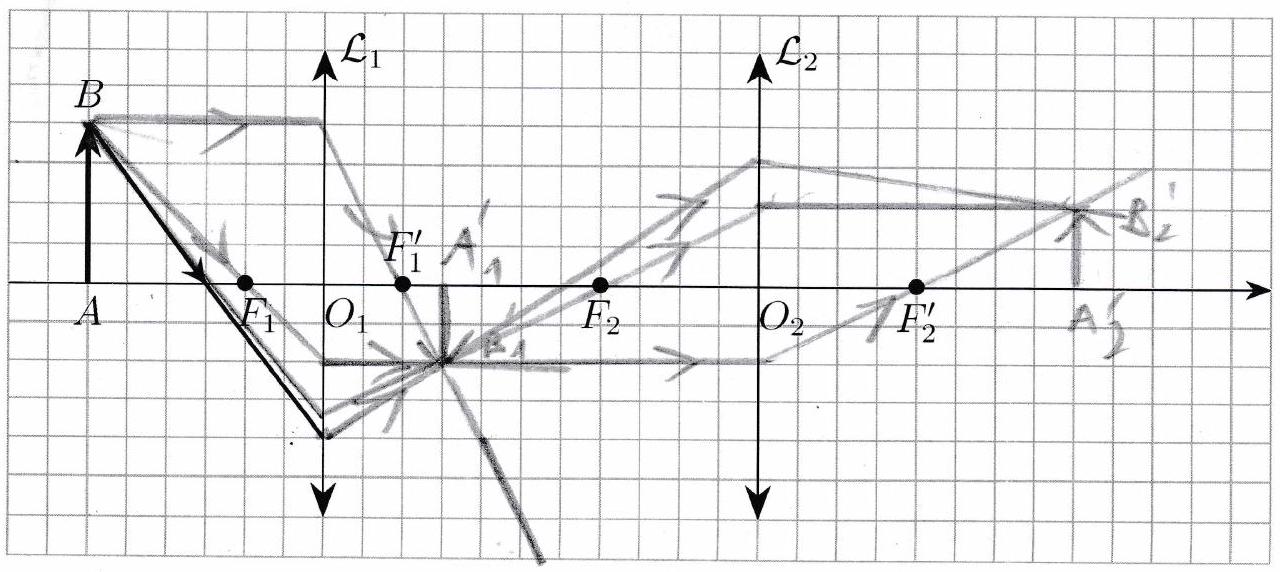
Application 6¶

1. Construire l’image $A_{2} B_{2}$ de $A B$ produite par le système optique ci-dessous.

2. Caractériser l’image.

3. Représenter la marche du rayon représenté en bleu à travers le système.

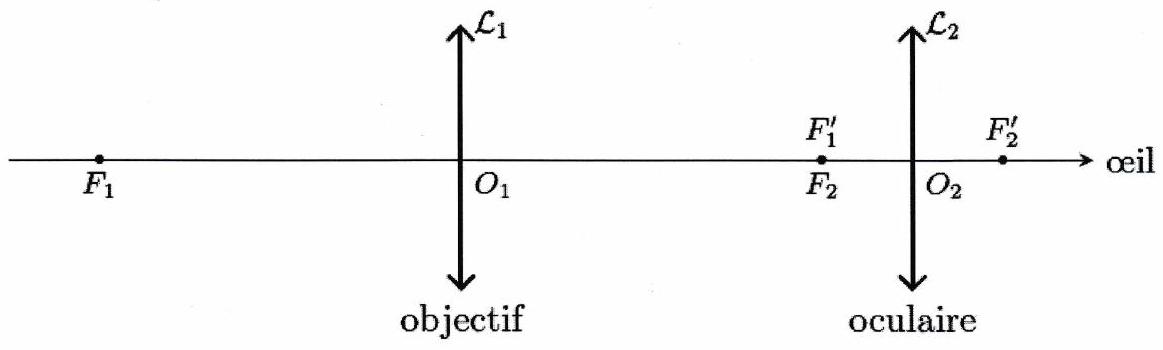
F ) Lunette astronomique¶

Une lunette astronomique permet d’obtenir une image agrandie d’un objet situé à l’infini. Elle est constituée de deux lentilles convergentes :

• un objectif $\mathcal{L}_{\infty}$ de grande distance focale $f_{1}^{\prime}$;

• un oculaire $\mathcal{L}_{\infty}$ de faible distance focale $f_{2}^{\prime}<f_{1}^{\prime}$.

Pour une observation confortable à l’œil nu, l’image est formée à l’infini : il s’agit d’un système afocal. Pour cela, le foyer image de l’objectif et le foyer objet de l’oculaire sont confondus $\left(F_{1}^{\prime}=F_{2}\right)$.

Application 7¶

On observe un objet ponctuel $A$ situé à l’infini à travers une lunette afocale d’objectif $L_{1}$ et d’oculaire $L_{2}$. Les rayons issus de $A$ forment un angle $\alpha$ avec l’axe optique de la lunette.

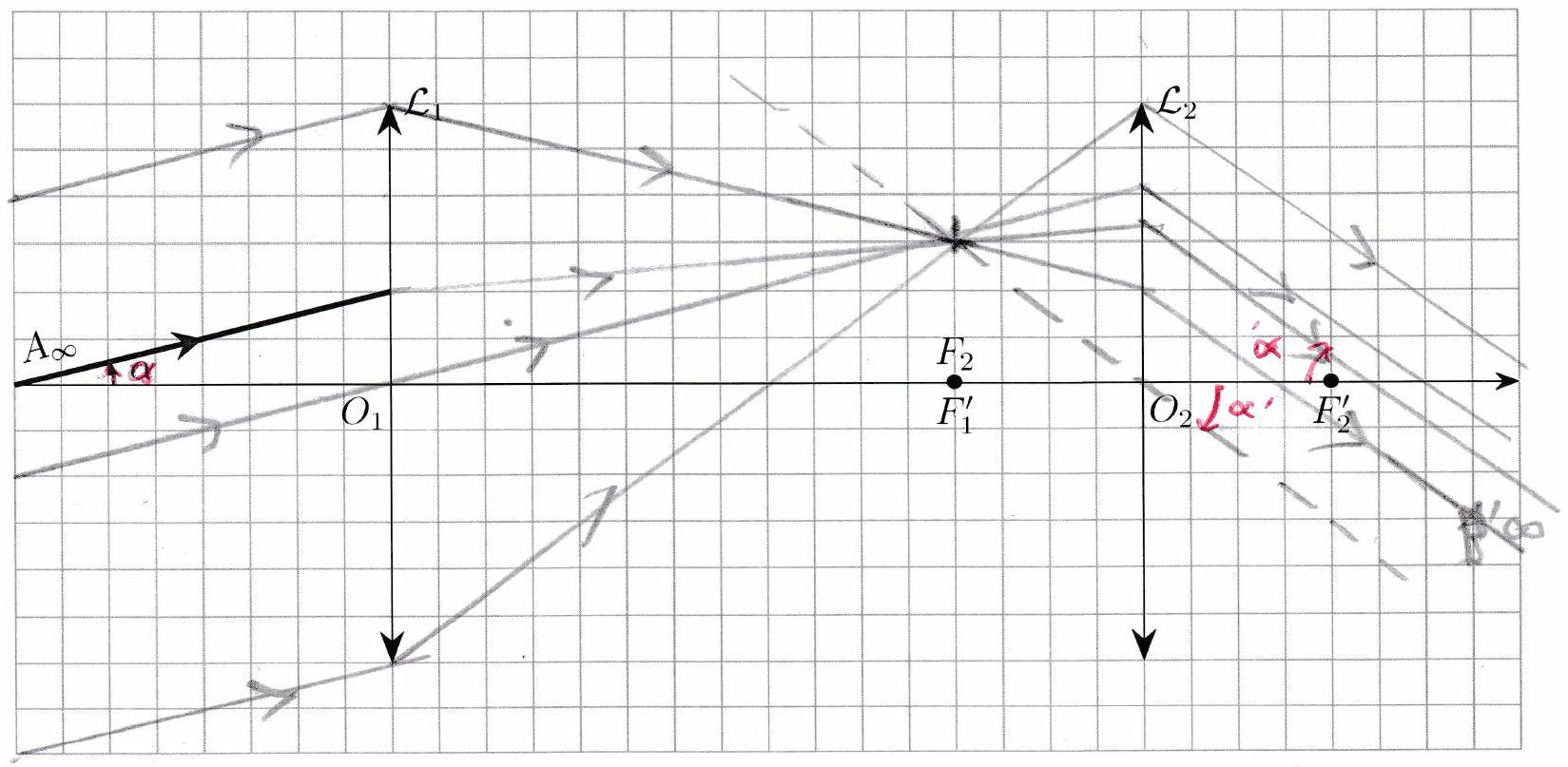
1. Construire l’image de $A$ par la lunette.

2. Représenter la marche du rayon rouge, puis celle du faisceau issu de $A$ délimité par les rayons passant par le bord de l’objectif.

Définition 21 : Système afocal¶

Un système afocal est un système optique qui transforme un faisceau de lumière parallèle en un autre faisceau de lumière parallèle : il ne possède pas de foyer objet, ni de foyer image.

La lunette doit par ailleurs fournir une image agrandie de l’objet visé. Puisque l’objet et l’image se trouvent à l’infini, on mesure quantitativement les performances d’une lunette par le grossissement.

Définition 22 : Grossissement¶

On définit le grossissement d’une lunette comme le rapport

où $\alpha$ est la taille angulaire (algébrique) de l’objet sans la lunette et $\alpha^{\prime}$ celle de son image à travers la lunette.