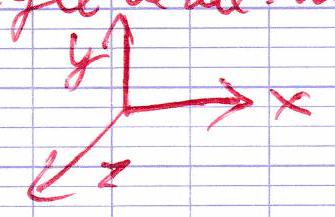Introduction à la cinématique
Introduction à la cinématique ¶ Vecteurs
Résolution
un vecteur sera déterminé par :
→ a norme
Graphiquement on le représentera par une flèche
Espace vectoriel
Un espace vectoriel ξ \xi ξ R \mathbb{R} R
Propriétés :
associativité ( u ⃗ + v ⃗ ) + w ⃗ = u ⃗ + ( v ⃗ + w ⃗ ) (\vec{u} + \vec{v}) + \vec{w} = \vec{u} + (\vec{v} + \vec{w}) ( u + v ) + w = u + ( v + w )
commutativité u ⃗ + v ⃗ = v ⃗ + u ⃗ \vec{u} + \vec{v} = \vec{v} + \vec{u} u + v = v + u
Relation de Chasles
∀ A , B , C A B → = A C → + C B → \forall A, B, C \quad \overrightarrow{AB} = \overrightarrow{AC} + \overrightarrow{CB} ∀ A , B , C A B = A C + CB
Base et dimension
Un ensemble de n n n ( e 1 → , e 2 → , … , e n → ) \left(\overrightarrow{e_{1}}, \overrightarrow{e_{2}}, \ldots, \overrightarrow{e_{n}}\right) ( e 1 , e 2 , … , e n ) ε \varepsilon ε ∀ u ⃗ ∈ ε \forall \vec{u} \in \varepsilon ∀ u ∈ ε
u ⃗ = λ 1 e 1 → + λ 2 e 2 → + … + λ n e n → ( λ i e ˊ tant uniques ) dim ( ε ) = n \begin{aligned}
& \vec{u} = \lambda_{1} \overrightarrow{e_{1}} + \lambda_{2} \overrightarrow{e_{2}} + \ldots + \lambda_{n} \overrightarrow{e_{n}} \\
& (\lambda_{i} \text{ étant uniques }) \text{dim}(\varepsilon) = n
\end{aligned} u = λ 1 e 1 + λ 2 e 2 + … + λ n e n ( λ i e ˊ tant uniques ) dim ( ε ) = n Cinématique Définition :
La cinématique est l’étude des mouvements d’un solide indépendamment des causes de ces mouvements.
Repérage dans l’espace
Repère
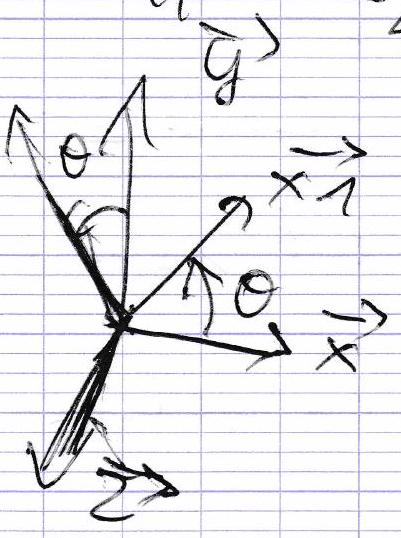
Il est possible de décrire de manière unique la position d’un point dans l’espace grâce à sa projection dans un repère constitué d’un point d’origine et de 3 vecteurs orthogonaux.
⇒ Repère orthonormé direct (règle de la main droite)
Repères classiques
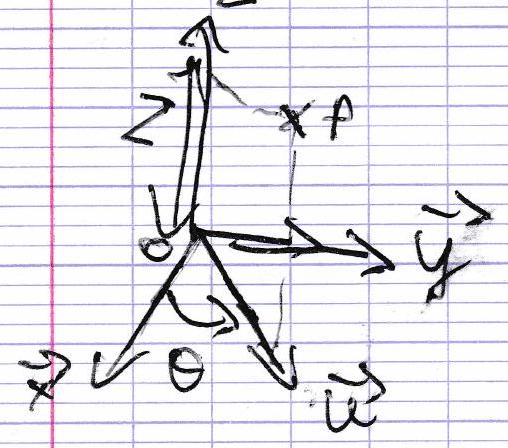
2.1) Repère cartésien
O P → = x x ⃗ + y y ⃗ + z z ⃗ \overrightarrow{OP} = x \vec{x} + y \vec{y} + z \vec{z} OP = x x + y y + z z (4) petit volume d x ⋅ d y ⋅ d z dx \cdot dy \cdot dz d x ⋅ d y ⋅ d z
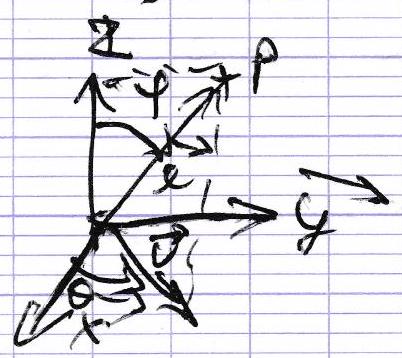
2.2) Repère cylindrique
O P → = r u ⃗ + z z ⃗ \overrightarrow{OP} = r \vec{u} + z \vec{z} OP = r u + z z r d r d θ d z r \, dr \, d\theta \, dz r d r d θ d z
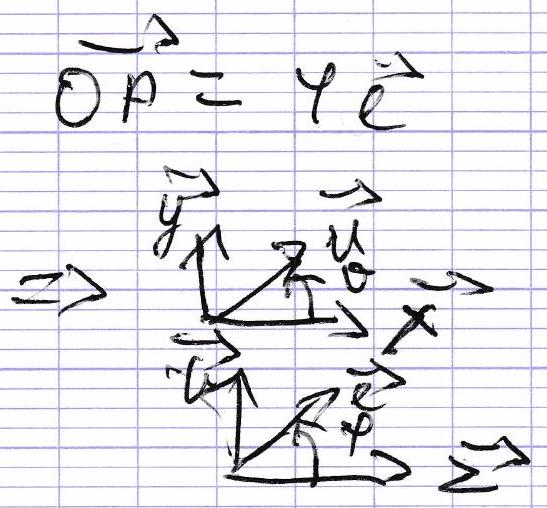
3.2) 3) → Repère sphérique
petit volume d r d φ sin φ d θ dr \, d\varphi \, \sin \varphi \, d\theta d r d φ sin φ d θ
Opérations sur les Vecteurs
If will
5) Dérivation vectorielle. ¶ Dérivation d’un vecteur défini dans une base dans cette même base
Soit u ⃗ ( t ) = a ( t ) x ⃗ + b ( t ) y ⃗ + c ( t ) z ⃗ \vec{u}(t) = a(t) \vec{x} + b(t) \vec{y} + c(t) \vec{z} u ( t ) = a ( t ) x + b ( t ) y + c ( t ) z B ( x ⃗ , y ⃗ , z ⃗ ) B(\vec{x}, \vec{y}, \vec{z}) B ( x , y , z )
( d u ⃗ ( t ) d t ) = d a ( t ) d t x ⃗ + d b ( t ) d t y ⃗ + d c ( t ) d t z ⃗ \left(\frac{d \vec{u}(t)}{dt}\right) = \frac{da(t)}{dt} \vec{x} + \frac{db(t)}{dt} \vec{y} + \frac{dc(t)}{dt} \vec{z} ( d t d u ( t ) ) = d t d a ( t ) x + d t d b ( t ) y + d t d c ( t ) z 5.2) Dérivation d’un vecteur défini dans une autre base que celle de dérivation
Soit u ⃗ 1 ( t ) = a ( t ) x ⃗ 1 + b ( t ) y ⃗ 1 + c ( t ) z ⃗ 1 \vec{u}_{1}(t) = a(t) \vec{x}_{1} + b(t) \vec{y}_{1} + c(t) \vec{z}_{1} u 1 ( t ) = a ( t ) x 1 + b ( t ) y 1 + c ( t ) z 1 B 1 ( x ⃗ 1 , y ⃗ 1 , z ⃗ 1 ) B_{1}(\vec{x}_{1}, \vec{y}_{1}, \vec{z}_{1}) B 1 ( x 1 , y 1 , z 1 )
( d u ⃗ 1 ( t ) d t ) B 2 = ( d u ⃗ 1 ( t ) d t ) B 1 + Ω ⃗ B 1 B 2 ∧ u ⃗ 1 ( t ) \left(\frac{d \vec{u}_{1}(t)}{dt}\right)_{B_{2}} = \left(\frac{d \vec{u}_{1}(t)}{dt}\right)_{B_{1}} + \vec{\Omega}_{B_{1}B_{2}} \wedge \vec{u}_{1}(t) ( d t d u 1 ( t ) ) B 2 = ( d t d u 1 ( t ) ) B 1 + Ω B 1 B 2 ∧ u 1 ( t ) y ⃗ \vec{y} y
Vitesse de rotation de B 1 B_{1} B 1 B 2 B_{2} B 2
⇒ Ω ⃗ B 1 B 2 = d θ ( t ) d t z ⃗ \Rightarrow \vec{\Omega}_{B_{1}B_{2}} = \frac{d\theta(t)}{dt} \vec{z} ⇒ Ω B 1 B 2 = d t d θ ( t ) z Dérivée d’une somme de vecteurs
( d ( u ⃗ + v ⃗ ) d t ) B = ( d u ⃗ d t ) B + ( d v ⃗ d t ) B \left(\frac{d (\vec{u} + \vec{v})}{dt}\right)_{B} = \left(\frac{d \vec{u}}{dt}\right)_{B} + \left(\frac{d \vec{v}}{dt}\right)_{B} ( d t d ( u + v ) ) B = ( d t d u ) B + ( d t d v ) B Dérivée d’un produit scalaire
( d ( u ⃗ ⋅ v ⃗ ) d t ) B = ( d u ⃗ d t ) B ⋅ v ⃗ + u ⃗ ⋅ ( d v ⃗ d t ) B \left(\frac{d (\vec{u} \cdot \vec{v})}{dt}\right)_{B} = \left(\frac{d \vec{u}}{dt}\right)_{B} \cdot \vec{v} + \vec{u} \cdot \left(\frac{d \vec{v}}{dt}\right)_{B} ( d t d ( u ⋅ v ) ) B = ( d t d u ) B ⋅ v + u ⋅ ( d t d v ) B Dérivée d’un produit vectoriel
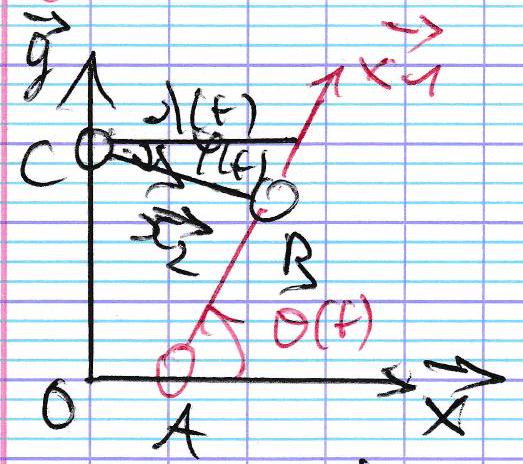
( d ( u ⃗ ∧ v ⃗ ) d t ) B = ( d u ⃗ d t ) B ∧ v ⃗ + u ⃗ ∧ ( d v ⃗ d t ) B \left(\frac{d (\vec{u} \wedge \vec{v})}{dt}\right)_{B} = \left(\frac{d \vec{u}}{dt}\right)_{B} \wedge \vec{v} + \vec{u} \wedge \left(\frac{d \vec{v}}{dt}\right)_{B} ( d t d ( u ∧ v ) ) B = ( d t d u ) B ∧ v + u ∧ ( d t d v ) B b) Fermeture de chaîne géométrique
{ O A → = l x ⃗ O C → = L y ⃗ C B → = λ ( t ) x ⃗ 2 A B → = R x ⃗ 1 \left\{
\begin{aligned}
& \overrightarrow{OA} = l \vec{x} \\
& \overrightarrow{OC} = L \vec{y} \\
& \overrightarrow{CB} = \lambda(t) \vec{x}_{2}
\end{aligned}
\right.
\quad \overrightarrow{AB} = R \vec{x}_{1} ⎩ ⎨ ⎧ O A = l x OC = L y CB = λ ( t ) x 2 A B = R x 1 lien λ ( t ) \lambda(t) λ ( t ) θ ( t ) \theta(t) θ ( t )
A ⃗ + A B → + B C → + C D → = 0 ⃗ ⇔ x ⃗ + R x ⃗ 1 − λ x ⃗ 2 − y ⃗ = 0 ⃗ ⇔ l x ⃗ + R ( cos ( θ ) x ⃗ + sin ( θ ) y ⃗ ) − λ ( cos ( φ ) x ⃗ + sin ( φ ) y ⃗ ) − L y ⃗ \begin{aligned}
& \vec{A} + \overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CD} = \vec{0} \\
\Leftrightarrow & \vec{x} + R \vec{x}_{1} - \lambda \vec{x}_{2} - \vec{y} = \vec{0} \\
\Leftrightarrow & l \vec{x} + R (\cos(\theta) \vec{x} + \sin(\theta) \vec{y}) \\
& - \lambda (\cos(\varphi) \vec{x} + \sin(\varphi) \vec{y}) - L \vec{y}
\end{aligned} ⇔ ⇔ A + A B + BC + C D = 0 x + R x 1 − λ x 2 − y = 0 l x + R ( cos ( θ ) x + sin ( θ ) y ) − λ ( cos ( φ ) x + sin ( φ ) y ) − L y ⇔ { l + R cos ( θ ) − λ cos ( φ ) = 0 R sin ( θ ) − λ sin ( φ ) − L = 0 ⇔ { λ cos ( φ ) = l + R cos ( θ ) λ sin ( φ ) = R sin ( θ ) − L En e ˊ levant au carr e ˊ et en additionnant : λ 2 = ( l + R cos ( θ ) ) 2 + ( R sin ( θ ) − L ) 2 \begin{aligned}
& \Leftrightarrow \left\{
\begin{array}{l}
l + R \cos(\theta) - \lambda \cos(\varphi) = 0 \\
R \sin(\theta) - \lambda \sin(\varphi) - L = 0
\end{array}
\right. \\
& \Leftrightarrow \left\{
\begin{array}{l}
\lambda \cos(\varphi) = l + R \cos(\theta) \\
\lambda \sin(\varphi) = R \sin(\theta) - L
\end{array}
\right. \\
& \text{En élevant au carré et en additionnant :} \\
& \lambda^{2} = (l + R \cos(\theta))^{2} + (R \sin(\theta) - L)^{2}
\end{aligned} ⇔ { l + R cos ( θ ) − λ cos ( φ ) = 0 R sin ( θ ) − λ sin ( φ ) − L = 0 ⇔ { λ cos ( φ ) = l + R cos ( θ ) λ sin ( φ ) = R sin ( θ ) − L En e ˊ levant au carr e ˊ et en additionnant : λ 2 = ( l + R cos ( θ ) ) 2 + ( R sin ( θ ) − L ) 2
