Introduction À LA CINÉMATIQUE - Livre chapeau - Cours prepa

3 Produit mixte¶

Soit $\vec{x}, \vec{y}$ et $\vec{z}$ trois vecteurs, le produit mixte est défini comme suit :

(\vec{x}, \vec{y}, \vec{z})=\vec{x} \cdot(\vec{y} \wedge \vec{z})

A noter : le produit mixte se conserve par permutation circulaire.

4 Double produit vectoriel¶

1 Produit scalaire¶

Soit $\vec{x}$ et $\vec{y}$ deux vecteurs alors

\vec{x} \cdot \vec{y}=\|\vec{x}\| \cdot\|\vec{y}\| \cdot \cos (\vec{x}, \vec{y})

avec, ( $\vec{x}, \vec{y}$ ) : l’angle orienté de $\vec{x}$ vers $\vec{y}$ . Si $\vec{x}$ et $\vec{y}$ sont définis comme suit

\begin{gathered} \vec{x}=x_{1} \vec{i}+x_{2} \vec{j}+x_{3} \vec{k} \\ \vec{y}=y_{1} \vec{i}+y_{2} \vec{j}+y_{3} \vec{k} \end{gathered}

alors

\vec{x} \cdot \vec{y}=x_{1} \cdot y_{1}+x_{2} \cdot y_{2}+x_{3} \cdot y_{3}

2 Produit vectoriel¶

Soit $\vec{x}$ et $\vec{y}$ deux vecteurs alors

\vec{x} \wedge \vec{y}=\|\vec{x}\| \cdot\|\vec{y}\| \cdot \sin (\vec{x}, \vec{y}) \cdot \vec{z}

avec, ( $\vec{x}, \vec{y}$ ) : l’angle orienté de $\vec{x}$ vers $\vec{y}$ . et $\vec{z}$ vecteur tel que ( $\vec{x}, \vec{y}, \vec{z}$ ) forme un trièdre direct ( $\vec{z}$ orthogonal aux deux autres vecteurs)

Soit $\vec{x}, \vec{y}$ et $\vec{z}$ trois vecteurs, alors :

\vec{x} \wedge(\vec{y} \wedge \vec{z})=(\vec{x} \cdot \vec{z}) \cdot \vec{y}-(\vec{x} \cdot \vec{y}) \cdot \vec{z}

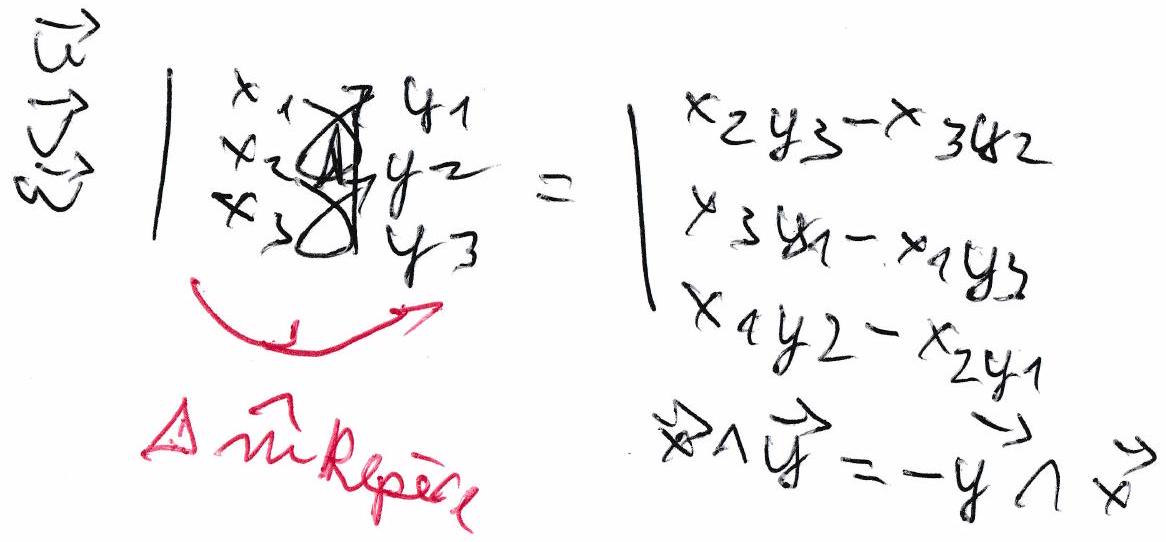
www.lyc-lakanal-sceaux.ac-versailles.fr