Performances des S.L.C.I. Cours 3¶

Lakanal Cité scolaire¶

^[1]

1 Fonction de transfert - Transmittance¶

Dans ce paragraphe, nous allons montrer que la connaissance et la maîtrise des 4 systèmes linéaires fondamentaux (que nous allons développer au paragraphe suivant) permet d’étudier tout autre système linéaire.

1.1 Obtention d’une fonction de transfert - Rappels¶

Nous étudions un système général, représenté par une équation différentielle linéaire à coefficients constants reliant une entrée $x(t)$ à une sortie $y(t)$ :

En supposant que toutes les conditions initiales sont nulles, la transformée de Laplace de cette équation nous donne :

Le rapport entre la sortie et l’entrée s’écrit:

$\mathrm{H}(\mathrm{p})$ est appelée fonction de transfert du système. La fonction de transfert du système est :

• une fraction rationnelle en p,

• entièrement caractérisée par ses pôles (racines du dénominateur) et ses zéros (racines du numérateur). Si cette fonction de transfert est entièrement définie, on peut prédire l’évolution temporelle de la sortie pour une entrée quelconque. En effet, la sortie $Y(p)$ (dans le domaine de Laplace) est définie par l’équation : $Y(p)=H(p) \cdot X(p)$ Pour obtenir la sortie $y(t)$ (dans le domaine temporel), il suffit de faire la transformée de Laplace inverse de $Y(p)$.

1.2 Forme et caractéristiques d’une fonction de transfert¶

1.2.1 Forme générale canonique d’une fonction de transfert¶

Une fonction de transfert quelconque est écrite sous la forme :

Nous allons factoriser le numérateur $N(p)$ et le dénominateur $D(p)$ de cette fonction de transfert.

Etape 1 : présence de racine(s) nulle(s) :¶

Si le dénominateur $D(p)$ possède une racine nulle :

• de multiplicité 1 alors il est possible de factoriser $D(p)$ par $p$,

• de multiplicité $k$ alors il est possible de factoriser $D(p)$ par $p^{k}$.

Autrement dit, dans le cas général, on peut réécrire le dénominateur par :

avec $n=k+q$

Etape 2 : factorisation par la constante :¶

Comme $c_{0} \neq 0$, on peut factoriser le polynôme $\mathrm{C}(\mathrm{p})$. On le réécrit par :

Etape 3 : présence de racine(s) réelle(s) :¶

Si le dénominateur $E(p)$ possède une racine réelle :

• $p=-\frac{1}{T_{i}}$ de multiplicité 1 alors il est possible de factoriser $E(p)$ par $\left(1+T_{i} \cdot p\right)$,

• $p=-\frac{1}{T_{j}}$ de multiplicité 2 alors il est possible de factoriser $E(p)$ par $\left(1+T_{j} \cdot p\right)^{2}, \ldots$

Autrement dit, dans le cas général, on peut réecrire le polynôme $E(p)$ par :

avec $q=v+r$

Etape 4 : présence de racines complexes conjuguées 2 à 2 :¶

Si le dénominateur $F(p)$ possède 2 racines complexes conjuguées 2 à 2 : $p \neq-\xi \cdot \omega_{0} \pm j \cdot \omega_{0} \cdot \sqrt{1-\xi^{2}}$ de multiplicité 1 alors il est possible de factoriser $F(p)$ par $\left(1+\frac{2 \xi}{\omega_{0}} \cdot p+\frac{p^{2}}{\omega_{0}^{2}}\right)$. Autrement dit, dans le cas général, on peut réécrire le polynôme $F(p)$ par :

avec $r=2 . w$

Factorisation complète du dénominateur :¶

En fonction de la présence de racine(s) nulle(s), de racine(s) réelle(s) et/ou de racines complexes conjuguées 2 à 2 , il est possible de factoriser le dénominateur $D(p)$ par :

Exemple :

Le numérateur peut aussi se factoriser de la même manière.

Conclusion¶

Nous pouvons donc mettre notre fonction de transfert sous la forme suivante :

Ceci montre que l’étude des systèmes de base (proportionnel, intégrateur, premier et deuxième ordre) est nécessaire et suffisante, pour avoir une idée du comportement de tous les types de systèmes linéaires.

1.2.2 Caractéristiques d’une fonction de transfert¶

Ordre d’un système :¶

Soit le système dont la transmittance générale peut être écrite sous la forme suivante :

On appelle ordre de ce système linéaire le degré du dénominateur $n=\alpha+l$

Classe du système :¶

Si l’entier relatif $\alpha=n-l$ est positif, alors $\alpha$ représente le nombre d’intégrations et on appelle $\alpha$ la classe du système.

Gain statique :¶

Pour tout les systèmes ci-dessus, sous condition $\alpha=0$ (pas d’intégrateur), dans le cas où toutes les limites écrites ci-dessous existent, on appelle $K_{S}$ le gain statique défini par le rapport :

Démonstration :

Lycée Lakanal - Sceaux

www.lyc-laka.nal-sceaux.ac-versailles.fr Lycée Lakanal - Sceaux

Page 4 / 12

2 Réponse temporelle des SLCI fondamentaux¶

©OSO

2.1 Modélisation des entrées¶

Pour étudier le comportement dynamique d’un système, il n’est pas toujours simple de traduire sous forme d’équations les lois de la physique qui régissent son comportement. Il est souvent plus efficace de le soumettre à des signaux tests et d’observer sa sortie. De plus, la définition des critères de performances se fait majoritairement à partir de ces signaux. On se propose ici de présenter les signaux les plus couramment utilisés(pour les temps négatifs, les signaux seront toujours considérés à valeur nulle).

2.1.1 Impulsion de Dirac $\delta(t)$¶

Si $t \neq 0, \delta(t)=0$ et si $t=0, \int_{-\infty}^{+\infty} \delta(t)=1$. Cette entrée permet de modéliser le comportement d’un choc, d’une impulsion. Elle est physiquement irréalisable. Elle peut être modélisée par la limite lorsque $\tau$ tend vers 0 de la fonction ci-contre. La réponse temporelle à un Dirac est appelée réponse impulsionnelle.

2.1.2 Echelon de Heaviside $u(t)$¶

L’échelon est le signal de base d’étude des systèmes asservis. Il permet d’étudier le comportement du système lorsqu’on lui applique une consigne constante. $u(t)=1$ lorsque $t$ est supérieur ou égal à $0, u(t)=0$ sinon.

2.1.3 Rampe¶

L’entrée en rampe d’un système permet d’étudier le comportement dynamique d’un système et principalement sa capacité à suivre une consigne variable

2.1.4 La sinusoïde¶

L’entrée sinusoïdale permet d’étudier le comportement fréquentiel du système en faisant varier la pulsation du signal.

2.1.5 Traitement des signaux composés de signaux élémentaires¶

Tout signal affine par morceaux peut s’écrire comme la somme de signaux élémentaires en utilisant des fonctions échelon et rampe, éventuellement retardées. Ces signaux composés sont souvent utilisés pour la commande des systèmes.

2.2 Systèmes Linéaires Fondamentaux¶

2.2.1 Systèmes proportionnels¶

Systèmes modélisable par un gain pur¶

Certains systèmes peuvent être modélisés par une constante, c’est à dire une relation de proportionnalité directe entre l’entrée et la sortie : $y(t)=K x(t)$. La constante de proportionnalité est alors appelée le gain du système.

Fonction de transfert¶

Dans le domaine de Laplace, la fonction de transfert d’un système proportionnel s’écrit : $H(p)=K$

2.2.2 Systèmes intégrateur¶

Un système intégrateur a pour équation : $\frac{d y(t)}{d t}=K . x(t)$

Fonction de transfert¶

Dans le domaine de Laplace, la fonction de transfert d’un système intégrateur s’écrit :

2.2.3 Systèmes du premier ordre¶

Un système du premier ordre a comme équation différentielle caractéristique :

avec $K$ gain du système et $T$ (en seconde) constante de temps du système.

Fonction de transfert¶

Dans le domaine de Laplace, la fonction de transfert d’un système du premier ordre s’écrit :

Réponse indicielle¶

Si l’on soumet un système du premier ordre à un échelon $x(t)=E . u(t)$, alors la sortie dans le domaine de Laplace a la forme suivante :

Ce qui nous donne dans le domaine temporel :

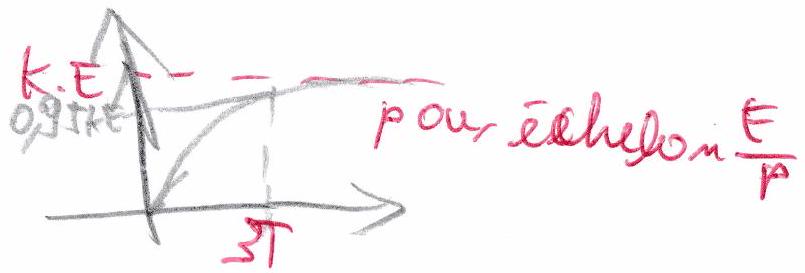
Réponse à une rampe¶

Si l’on soumet un système du premier ordre à un échelon $x(t)=$ a.t. $u(t)$, alors la sortie dans le domaine de Laplace a la forme suivante :

Ce qui nous donne dans le domaine temporel :

$$

y(t)=K \cdot a\left((t-T)+T e^{-\frac{t}{T}}\right) u(t) $$

2.2.4 Système du second ordre¶

Un système du second ordre a comme équation différentielle caractéristique :

avec $K$ le gain statique du système, $\omega_{0}$ (en rad. $\mathrm{s}^{-1}$ ) la pulsation propre non amortie et $\xi$ (sans unité) le facteur d’amortissement.

Fonction de transfert¶

Dans le domaine de Laplace, la fonction de transfert d’un système du deuxième ordre s’écrit :

Réponse indicielle¶

Si l’on soumet un système du deuxième ordre à un échelon $x(t)=E . u(t)$, alors la sortie dans le domaine de Laplace a la forme suivante :

Les valeurs initiale (0) et finale (K.E) de la sortie ne dépendent pas de $\xi$ et $\omega_{0}$. Par contre, l’allure de la réponse temporelle dépend de la nature des racines (réelles ou complexes) du dénominateur. a) Cas $\xi>1$ deux racines réelles

La sortie est alors de la forme suivante :

Ce qui nous donne dans le domaine temporel :

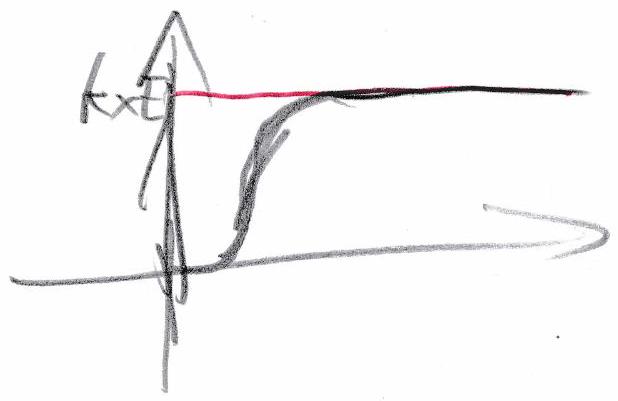
b) Cas $\xi=1$ : une racine double

La sortie est alors de la forme suivante :

Ce qui nous donne dans le domaine temporel :

3 Performances des SLCI
\section*{\section*{I}}¶

3.1 Les systèmes du premier ordre¶

3.1.1 Influence des paramètres caractéristiques¶

Nous venons de voir que la fonction de transfert d’un système du premier ordre est : $H(p)=\frac{K}{1+T p}$ et que sa réponse temporelle d’un système du premier ordre à un échelon d’amplitude $E$ est :

ou après avoir posé $\omega_{p}=\omega_{0} \sqrt{1-\xi^{2}}$ pseudo pulsation Ce qui nous donne dans le domaine temporel :

Ce qui nous donne dans le domaine temporel :

c) Cas $0<\xi<1$ : deux racines complexes conjuguées La sortie est alors de la forme suivante :
c) Cas $0<\xi<1$ : deux racines com¶

. $Y$

"

$$

$$

• -敖 ou après avoir posé $\omega_{p}=\omega_{0} \sqrt{1-\xi^{2}}$ pseudo pulsation

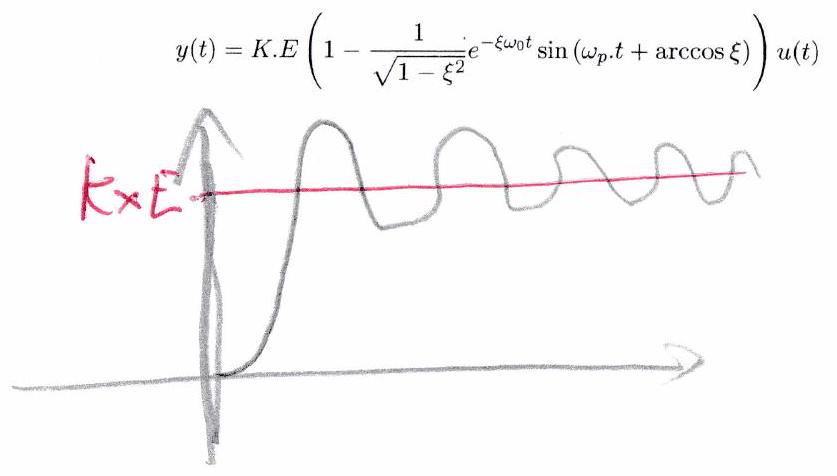
rdre "

"

Observons sur la figure ci-dessous les paramètres caractéristiques d’un premier ordre :

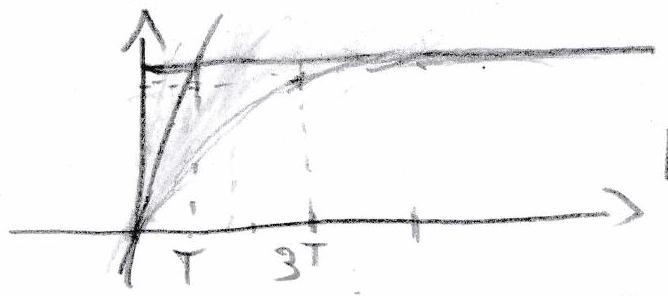
Et voici comment ces paramètres influencent la réponse indicielle :

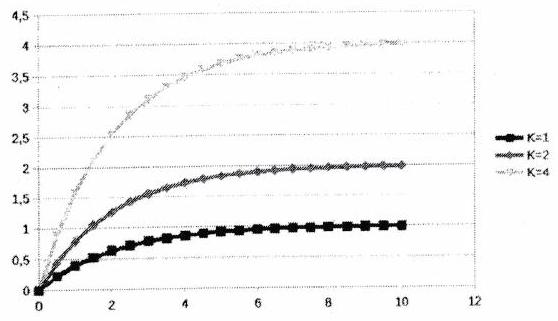
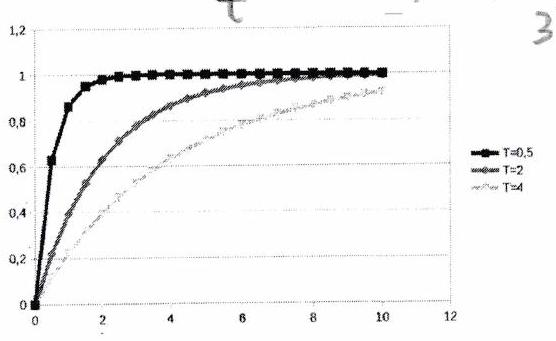
3.1.2 Performances d’un premier ordre¶

Stabilité Tant que la constante de temps T est positive, un système du premier ordre est inconditionnellement stable. En effet, l’expression $y(t)=K E\left(1-e^{-\frac{t}{T}}\right)$ converge tant que $T>0$.

Amortissement La réponse temporelle d’un système du premier ordre soumis à un échelon ne possède pas de dépassement.

Rapidité Le temps de réponse à $5 \%$ de la réponse indicielle d’un système du premier ordre est : $t_{5 \%}=3 . T$.

Précision L’erreur statique sera nulle si et sculement si le gain statique du système du premier ordre (en boucle fermée) vaut : $K=1$.

3.1.3 Identification¶

Dans le cadre des systèmes asservis, l’entrée type la plus communément utilisée est l’échelon. Si la réponse mesurée présente les caractéristiques de la réponse indicielle d’un système du 1er ordre (allure à décroissance exponentielle, pente initiale non nulle, pas d’oscillations hors éventuel bruit de mesure et convergence vers une valeur constante), alors il est raisonnable de modéliser le comportement de ce système par une équation différentielle du 1er ordre. Les paramètres $T$ et $K$ sont alors identifié sur la courbe représentant la sortie. www.lyc-lakanal-sceaux.ac-versailles.fr

3.2 Les systèmes du deuxième ordre¶

3.2.1 Influence des paramètres caractéristiques¶

Nous avons vu que la fonction de transfert de’un système du deuxième ordre est :

Pour déterminer la réponse temporelle d’un système du second ordre soumis à un échelon d’amplitude e0, il faut distinguer deux cas en fonction de la nature des pôles de $H(p)$. Si $H(p)$ possède :

• 2 pôles réels $(\xi>1)$, alors on dira alors que l’on est en régime apériodique,

• 2 pôles complexes conjugués $(\xi<1)$, alors on dira que l’on est en régime pseudo-périodique.

Régime apériodique¶

L’expression de la réponse temporelle apériodique d’un système du deuxième ordre soumis à un échelon d’amplitude $E$

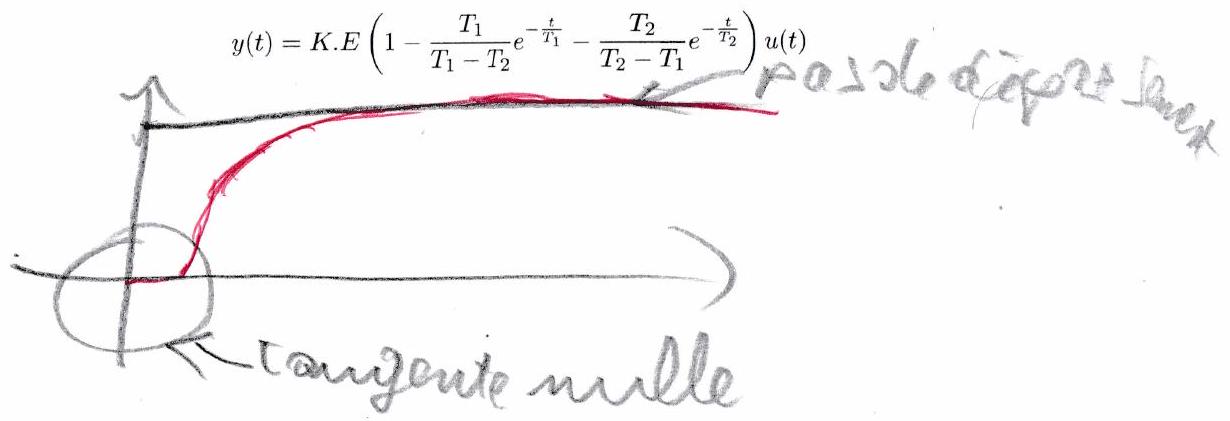
Propriétés remarquables :

• la pente de la tangente à l’origine est nulle.

• il n’y a pas de dépassement, le système est amorti. On parle de régime apériodique.

• si $\left|T_{2}\right|$ grand devant $\left|T_{1}\right|$, on peut alors assimiler la courbe du système à celle d’un premier ordre de constante de temps $T=T_{2}$ (avec un retard égal à $T_{1}$ )

• plus $\xi$ est proche de 1 , plus le système est rapide.

Régime pseudo-périodique¶

L’expression de la réponse temporelle est la suivante :

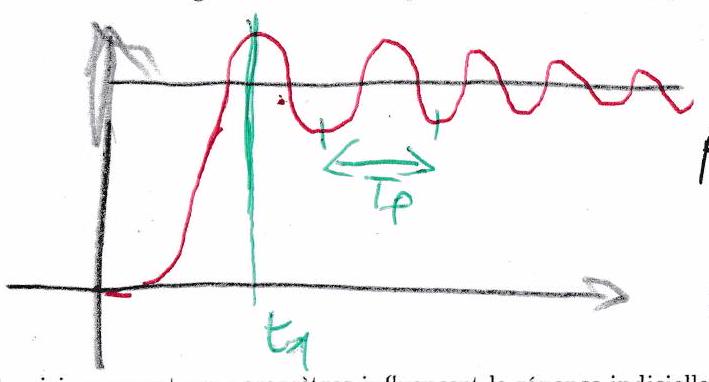
Et voici comment ces paramètres influencent la réponse indicielle :

Observons sur la figure ci-dessous les paramètres caractéristiques de ce régime.

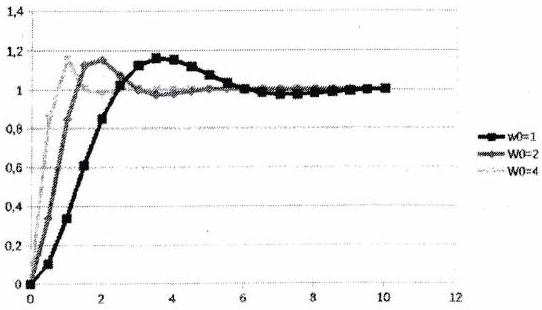
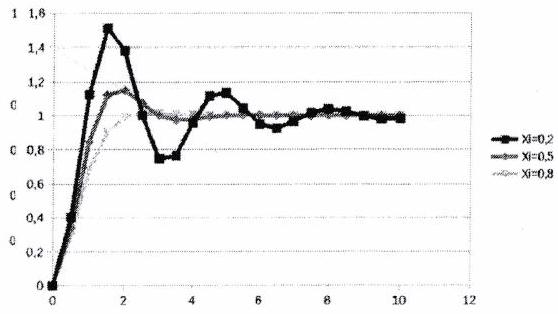
Le système le plus rapide est obtenu pour un amortissement $\xi=0,69$. Pour cette valeur, le premier dépassement en pourcentage vaut environ 0,05 . Les abaques ci-dessous, nous montre l’évolution du dépassement et du temps de réponse en fonction de $\xi(z)$.

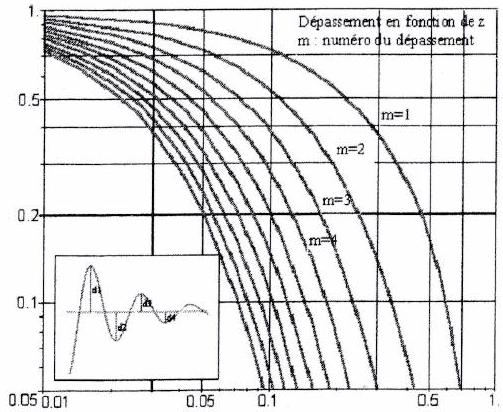
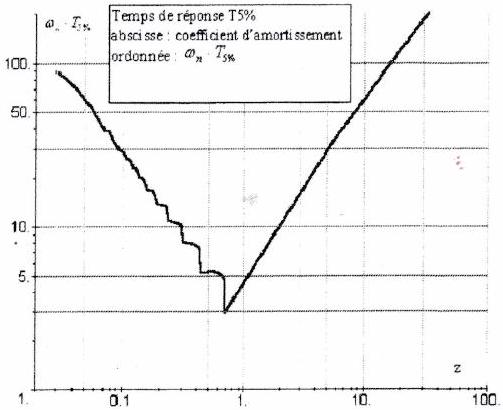
3.2.2 Performances d’un deuxième ordre¶

Stabilité Tant que le coefficient d’amortissement $\xi$ est positif, un système du deuxième ordre est inconditionnellement stable, il y a convergence de la réponse.

Rapidité Le temps de réponse à $5 \%$ de la réponse indicielle d’un système du deuxième ordre dépend de 2 paramètres : $\xi$ et $\omega_{0}$. C’est grâce à l’abaque du temps de réponse réduit (page précédente) que l’on pourra déterminer le temps de réponse à $5 \%$ du système connaissant les 2 paramètres.

Amortissement La réponse temporelle d’un système du deuxième ordre soumis à un échelon possède un dépassement à la seule condition que $\xi<1$.

Précision L’erreur statique sera nulle si et seulement si le gain statique du système du deuxième ordre vaut : $K=1$.

3.2.3 Identification de modèle¶

Dans la même démarche de modélisation comportementale que celle développée pour un premier ordre, si la réponse mesurée expérimentalement présente une tangente à l’origine nulle et des dépassements, le modèle du premier ordre ne peut plus convenir et il devient raisonnable de modéliser le comportement du système par une fonction de transfert du 2e ordre. Les paramètres caractéristiques sont alors déterminer à l’aide de la courbe de la réponse temporelle et/ou grâce à l’abaque des dépassements.