2 Systèmes linéaires continus invariants
2 Systèmes linéaires continus invariants¶
2.1 Systèmes linéaires¶
Un système linéaire est un système pour lequel les relations entre les grandeurs d’entrée et de sortie peuvent se mettre sous la forme d’un ensemble d’équations différentielles à coefficients constants.
Les systèmes linéaires possèdent principalement deux propriétés : la proportionnalité et l’additivité.
2.1.1 Principe de proportionnalité¶
l’intervention de l’homme. Pour réaliser la modélisation d’un système technique, il faut successivement :
isoler de façon globale le système (définir la frontière),
découper ce système en sous-systèmes autant de fois qu’il sera nécessaire,
associer à chacun des sous-systèmes un modèle de connaissance ou de comportement.
Un modèle de connaissance est obtenu en utilisant les lois qui régissent le fonctionnement (relation entrée-sortie) des différents sous-systèmes. Cette modélisation est analytique et possède un sens physique important. Un modèle de comportement est obtenu à partir d’une identification expérimentale de la loi entréesortie du mécanisme. Le mécanisme est alors considéré comme une boite noire. Les équations caractérisant le comportement n’ont pas de fondement physique. Les modèles de comportement ont, en général, un domaine de validité restreint. On modélisera en première approche un système sous la forme suivante :
Bien que les systèmes automatisés puissent gérer plusieurs sorties en fonction de plusieurs entrées principales, nous nous limiterons, pour des raisons de simplicité, aux systèmes ne possédant qu’une seule entrée et qu’une seule sortie. Ces systèmes sont dits mono-variables. Si votre système fonctionne avec plusieurs entrées (ou une entrée et des perturbations), il est possible, dans certains cas, d’étudier séparément la relation entre la sortie et chacune des entrées, puis de superposer, dans un second temps, les effets de chaque entrée.

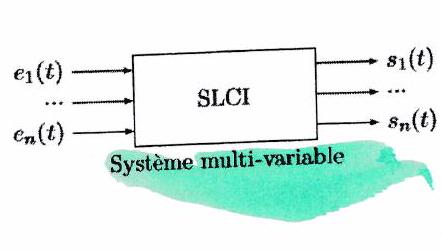

Un système automatisé est un ensemble d’éléments agencés pour exécuter une tâche donnée sans
\section*{1 Généralités}
Lyce¶



"
3.2 Comment traiter le cas de non-linéarités?¶
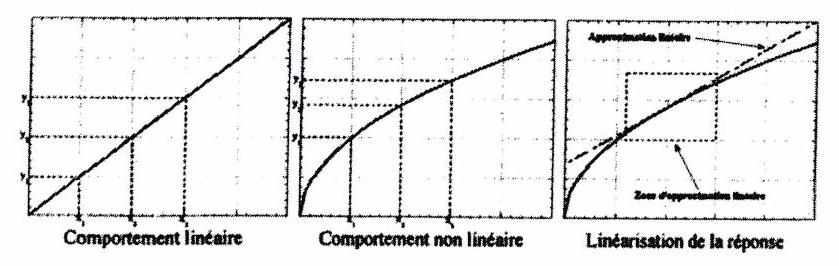
La plus part des systèmes physiques ne sont pas linéaires sur toute la totalité de leur domaine d’application. Cependant dans de nombreux cas, ils ne sont utilisés que sur une plage réduite de leur domaine. Sous ces conditions, il est possible en général d’approcher le comportement par un modèle linéaire. Le système est dit alors linéarisé.
4 Caractéristiques souhaitées d’un système linéaire¶
Le comportement d’un système asservi est évalué suivant différents critères de performance :
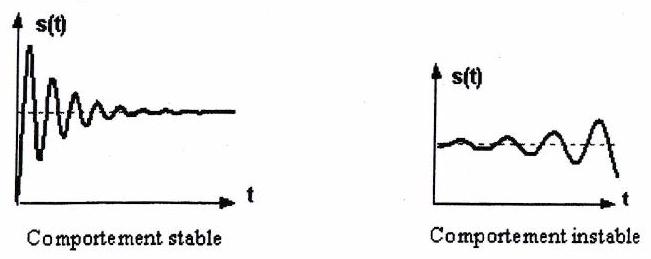
Stabilité : la réponse du système converge-t-elle pour une entrée constante? Certains systèmes peuvent être instables, dans ce cas, leurs réponses divergent ou oscillent sans jamais se stabiliser.
Précision : le système asservi atteint-il la valeur de consigne en l’absence de perturbation(s) ? Le système asservi atteint-il la valeur de consigne en présence de perturbation(s) ?
Rapidité : combien de temps faut-il au système pour se stabiliser?
Sachant que la réponse dépend évidement du signal d’entrée, les niveaux de ces performances sont généralement évalués à partir de la réponse à une entrée standard : une entrée constante nommée échelon.
4.1 Stabilité¶
Un système est stable si à une entrée bornée correspond une sortie bornée.
4.2 Caractérisation des systèmes stables¶
4.2.1 Amortissement¶
L’amortissement est caractérisé par le rapport entre les amplitudes successives des oscillations de la sortie. Plus ces oscillations s’atténuent rapidement, plus le système est amorti.
Taux de dépassement relatif : On caractérise le degré d’amortissement d’un transitoire par les dépassements successifs , etc.. On considère surtout le premier dépassement , défini sur la figure ci-dessous.
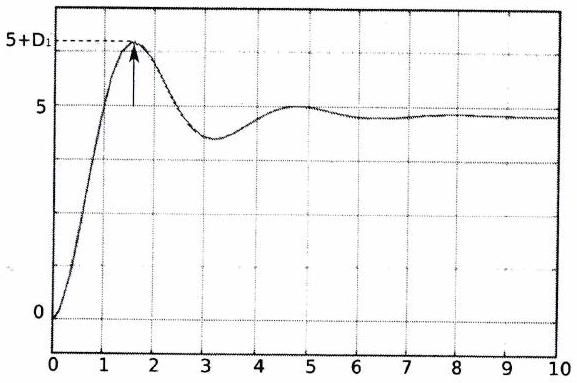
Pour qu’un système soit suffisamment amorti, on prescrira que son dépassement ne doit pas excéder un certain pourcentage de la valeur définitive de .
On calcule le taux de dépassement relatif (en pourcentage) qui caractérise l’amplitude maximale de la première oscillation de la manière suivante:
avec l’amplitude du premier dépassement (maximal pour un système stable) et la valeur à convergence (asymptotique) de la réponse.
4.2.2 Rapidité¶
Un système est dit rapide s’il converge en un temps court au regard de son contexte d’utilisation. Dans la plupart des cas, la valeur finale est atteinte de manière asymptotique voire oscillante, on retient alors comme critère d’évaluation de la rapidité d’un système, le temps de réponse à .
Temps de réponse à Dans la pratique, c’est le temps de réponse à (noté ou ) qui est le plus souvent utilisé. Il correspond au temps mis par le système pour atteindre la valeur à convergence appelée aussi valeur finale (donc en régime permanent) à près et à y rester.
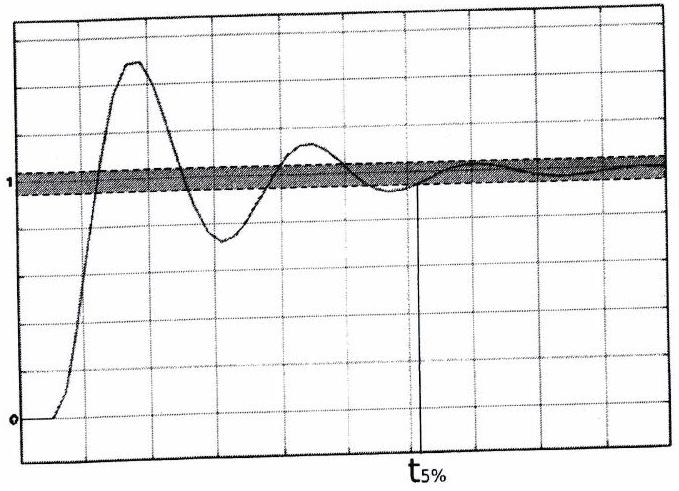
4.2.3 Précision¶
La précision d’un système qualifie son aptitude à atteindre la valeur visée (consigne), indépendamment des éventuelles perturbations. Elle est caractérisée par l’erreur en régime permanent qui correspond à l’écart entre la valeur de la consigne visée et la valeur réellement atteinte par la grandeur de sortie.
Si en régime permanent, la sortie diffère de l’entrée, on dit qu’il y a une erreur (ou un écart) permanente. Cas de l’échelon Dans le cas d’un essai en échelon (essai indiciel) l’erreur permanente s’appelle l’écart statique ou erreur indicielle ou erreur de position. Il est naturellement souhaitable que cette erreur soit nulle.
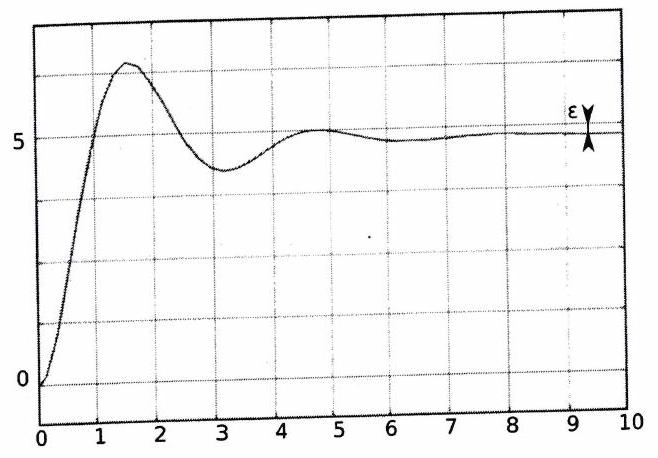
Cas de la rampe Dans le cas d’un essai en rampe, l’erreur en régime permanent s’appelle erreur de traînage. Elle peut être infinie (le système ne suit pas l’entrée), finie ou nulle. On désire de manière générale, qu’elle soit nulle ou du moins aussi petite que possible.
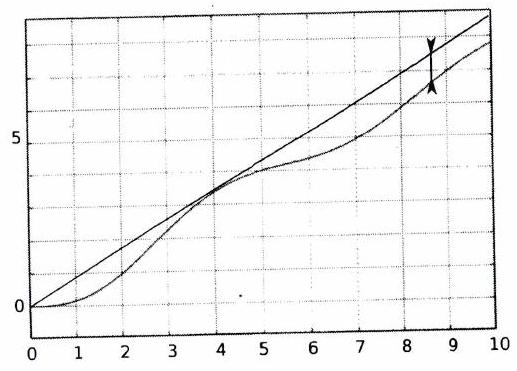
4.2.4 Sensibilité aux perturbations¶
Un système est dit sensible aux perturbations s’il he converge pas vers la même valeur selon qu’une perturbation extérieure est présente ou non.
Remarque La sensibilité aux perturbations n’est définie que pour les valeurs à convergence, donc en régime permanent, et non en régime transitoire.
4.2.5 Bilan¶
Un système automatisé idéal est un système qui aurait une bonne stabilité, une bonne précision et un régime transitoire rapide et bien amorti. De tels critères de performance ne sont (malheureusement) pas toujours compatibles. Tout l’art de l’automaticien sera de réaliser une partie commande permettant de respecter au mieux ces critères.
5 Les systèmes asservis¶
5.1 Systèmes asservis ou asservissements¶
Les signaux traités sont analogiques ou numériques et leurs valeurs des grandeurs d’entrée (causes) ne peuvent pas être prédéterminées à l’avance pour une grandeur de sortie imposée (effet). Une mesure du signal de sortie est réalisée en permanence, sa valeur est comparée à l’entrée puis corrigée. Il est possible de classer les systèmes asservis en deux grandes familles :
Les systèmes régulateurs : Ces systèmes doivent permettre le maintient d’une sortie constante pour une consigne d’entrée constante en luttant contre les perturbations (régulateur de vitesse automobile, régulation en température d’une four...).
Les systèmes suiveurs ou en poursuite : Ces systèmes sont conçus pour ajuster en permanence le signal de sortie au signal d’entrée qui varie en permanence (traqueur solaire. ..)
5.2 Représentation d’un système asservi : Schéma bloc¶
Le comportement du système peut être décrit par le schéma bloc suivant :

On constate que le système asservi est bouclé. Le bouclage apparaît chaque fois qu’au cours d’une opération, le système prend en compte l’observation de son état pour le modifier. Le bouclage est nécessaire dans les opérations où :
la précision mise en jeu est importante. L’observation de la grandeur à asservir permet de constater un écart ou une dérive quelconque par rapport à la référence souhaitée et donc de réagir en conséquence. Dans une solution sans bouclage on est amené à faire a priori des hypothèses quant au comportement de certains éléments, toute variation par rapport au comportement présupposé entraîne irrémédiablement un défaut sur le résultat final. On remarque ici que la précision du résultat final dépend essentiellement de la précision avec laquelle est faite l’observation.
des perturbations interviennent en cours d’opération modifiant ainsi l’état du système. Par exemple, l’ouverture de la porte d’un four thermostaté entraîne une déperdition de chaleur et donc une baisse de la température que l’on compense en augmentant la puissance de chauffage. Dans les cas d’un système bouclé, l’observation de la grandeur de sortie rendra compte de l’apparition d’une telle perturbation.
le comportement su système est mal connu ou variable. Ainsi, en électronique, le bouclage d’un amplificateur opérationnel conduit à un comportement tel que la relation entrée-sortie soit beaucoup moins sensible aux variations de gain de l’amplificateur seul non bouclé. Dans le cas de réalisations en série, on évite ainsi des opérations de tri sévère sur les composants, tout en garantissant des performances minimales pour chaque réalisation.
la stabilité est en cause. Soit que l’on souhaite stabiliser un système naturellement divergent, soit que l’on souhaite améliorer un comportement dynamique insatisfaisant (comportement trop lent par exemple). Ces différents besoins peuvent naturellement coexister dans certains cas.
5.3 Structure classique d’un système asservi¶
5.3.1 Notion de perturbation :¶
Aux entrées principales (consignes), s’ajoutent très souvent des entrées secondaires qui nuisent au bon fonctionnement du système étudié. Ces entrées sont appelées perturbations. Les perturbations modifient le signal de sortie de façon incontrôlable et imprévisible. Dans toutes les analyses de système que vous ferez, il faudra distinguer :
les grandeurs de consignes : les entrées sur lesquelles on peut agir de façon volontaire (ici ),
les perturbations : les entrées sur lesquelles nous n’avons aucun contrôle (ici ).
5.3.2 Précisions sur la structure d’un système :¶
La structure d’un système asservi comporte obligatoirement :
un traitement associé à un comparateur,
une chaîne d’action (actionneur - processus physique),
une chaîne d’observation (capteur - traitement du signal).
De manière plus précise, on retrouve souvent la structure générale ci-dessous :
une entrée principale (consigne ), éventuellement une entrée secondaire (perturbation et une sortie (signal commandé ),
un signal de commande, , un signal de retour, , et le signal d’erreur, .
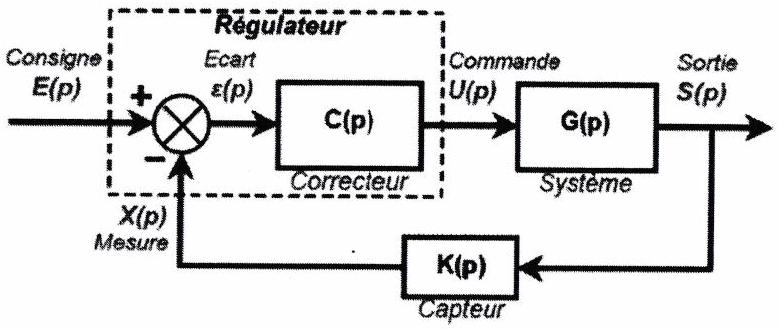
www
2 Fonction de Transfert en Boucle Ouverte et/ou Fermée¶
Nous souhaitons mettre en place une méthode efficace pour déterminer la fonction de transfert globale d’un système complexe en vue de déterminer ultérieurement les performances de ce système complexe.
2.1 Présentation du problème¶
La représentation par schéma bloc permet de représenter de manière graphique un système linéaire. Chaque bloc du schéma représente une des fonctions du système (un des constituant). A chacun des bloc, on associera la fonction de transfert du constituant qu’il représente. Les flèches reliant les blocs entre-eux représentent les informations d’entrée et de sortie des blocs. On détermine la fonction de transfert de chaque constituant à l’aide de l’équation différentielle décrivant son comportement, et de la transformée de Laplace. Le système d’équations est ainsi remplacé par un schéma comportant un ensemble de blocs représentant les constituants du système.
1.1 Objectif¶
On cherche à déterminer la fonction de transfert globale du système complexe de la forme :
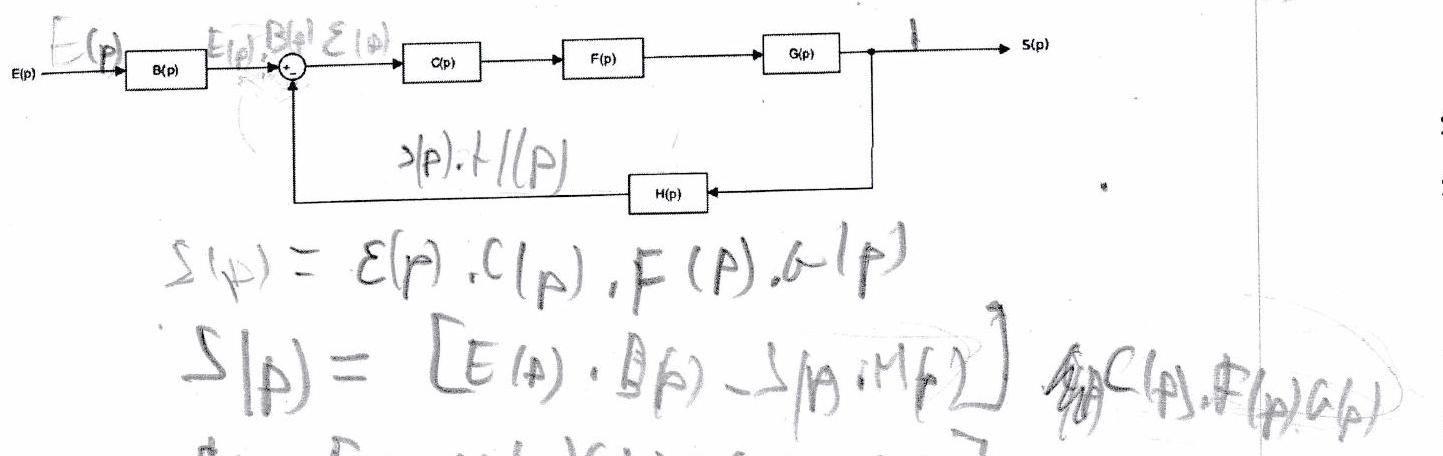
"
\section*{1 Schéma fonctionnel ou schéma-bloc}
1 Schéma fonctionnel ou schéma-bloc
,的
-¶
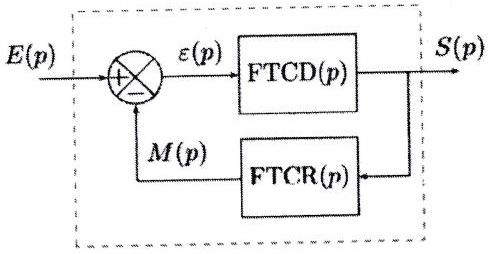
ion pa hém e. cs La représentation bloc du sc 7 - utilise les notations suivantes:
: signal de sortie de la boucle,
: signal d’entrée de la boucle,
: signal d’erreur de la boucle,
: signal de retour de la boucle.
L’objectif est de mettre en place une démarche graphique efficace pour déterminer la fonction de transfert équivalente telle que (on verra par la suite que l’on appellera ultérieurement Fonction de Transfert en Boucle Fermée).
Pour cela on utilisera 3 nouvelles Fonctions de transfert appelées:
Fonction de Transfert en Chaine Directe FTCD(p),
Fonction de Transfert en Chaine Retour FTCR(p),
Fonction de Transfert en Boucle Ouverte FTBO(p). 2.2 Définitions 2.2.1 Fonction de transfert en chaine directe
La chaîne directe est constituée des blocs reliant l’entrée et la sortie : on note,
2.2.2 Fonction de transfert en chaine retour¶
La chaîne retour est constituée des blocs reliant la sortie au comparateur : on note,
www
2.2.3 Fonction de transfert en boucle ouverte¶
On appelle fonction de transfert en boucle ouverte,
2.2.4 Fonction de transfert en boucle fermée¶
On appelle fonction de transfert en boucle fermée,
3 Manipulation de schémas blocs¶
3.1 Blocs en cascade¶

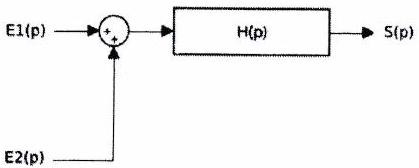
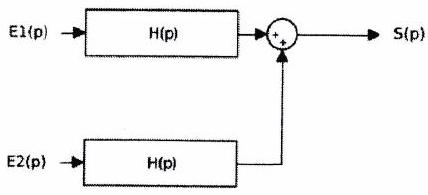
3.2 Blocs en parallèle¶

3.3 Structure en boucle fermée¶

3.4 Déplacements des points de prélèvement¶


3.5 Déplacements des sommateurs¶

3.6 Exemple¶
www