Chapitre 6 : Évolution temporelle d’un système chimique

Thermodynamique d’une réaction : description du sens d’évolution et de l’état final (= quand les compositions ne changent plus à l’échelle macroscopique) $\Rightarrow$ ligne $t_{\text{final}}$ d’un tableau d’avancement.

Cinétique de cette réaction : évolution des quantités de matière au cours du temps $t$ (vitesse de réaction) $\Rightarrow$ ligne intermédiaire « $t$ » d’un tableau d’avancement.

$\triangle$ Notations importantes : « $t$ » pour le temps, « $T$ » pour la température !

1 Vitesses d’une réaction chimique¶

Soit une réaction formelle $0 = \sum_{i} v_{i} A_{i}$ avec $v_{i}$ le coefficient stœchiométrique algébrique du constituant $A_{i}$ :

$v_{i} > 0$ si $A_{i}$ est un produit
$v_{i} < 0$ si $A_{i}$ est un réactif

1.1 Vitesse volumique de réaction (ou vitesse de la réaction)¶

Rappel : Avancement de la réaction : $\xi(t) = \frac{n_{i}(t) - n_{i, 0}}{v_{i}}$ S’exprime en mol.

La vitesse de réaction est la vitesse volumique de variation de $\xi$ :

v = \frac{1}{V} \frac{d \xi(t)}{dt}

(1)

NB : l’unité de temps du système international est la seconde mais il est courant d’utiliser des unités plus adaptées à l’échelle d’observation : minute, heure, années, siècle... (décroissances radioactives par exemple).

1.2 Vitesses volumiques relatives à chaque espèce (apparition/disparition)¶

	Vitesse volumique de disparition du réactif $A_{j}$	Vitesse volumique de formation du produit $A_{k}$
Définition générale : grandeur instantanée et positive	$v_{disp, A_j} = -\frac{1}{V} \frac{dn_{A_j}}{dt} = -\frac{d[A_j]}{dt}$	$v_{form, A_k} = \frac{1}{V} \frac{dn_{A_k}}{dt} = \frac{d[A_k]}{dt}$

Relation entre vitesse de réaction et vitesse d’apparition/disparition :

On a $d\xi(t) = \frac{dn_{A_i}(t)}{v_i}$

Donc pour un réactif $A_j$ :

v = -\frac{1}{|v_j|} \frac{d[A_j]}{dt} = \frac{1}{|v_j|} v_{disp, A_j}

(2)

Pour un produit $A_k$ :

v = \frac{1}{v_k} \frac{d[A_k]}{dt} = \frac{1}{v_k} v_{form, A_k}

(3)

Si la réaction a lieu dans le sens direct, toutes les vitesses sont positives.

Avez-vous tout compris ? - $n^{\circ} 1$ ¶

1.3 Identification graphique de la vitesse de réaction¶

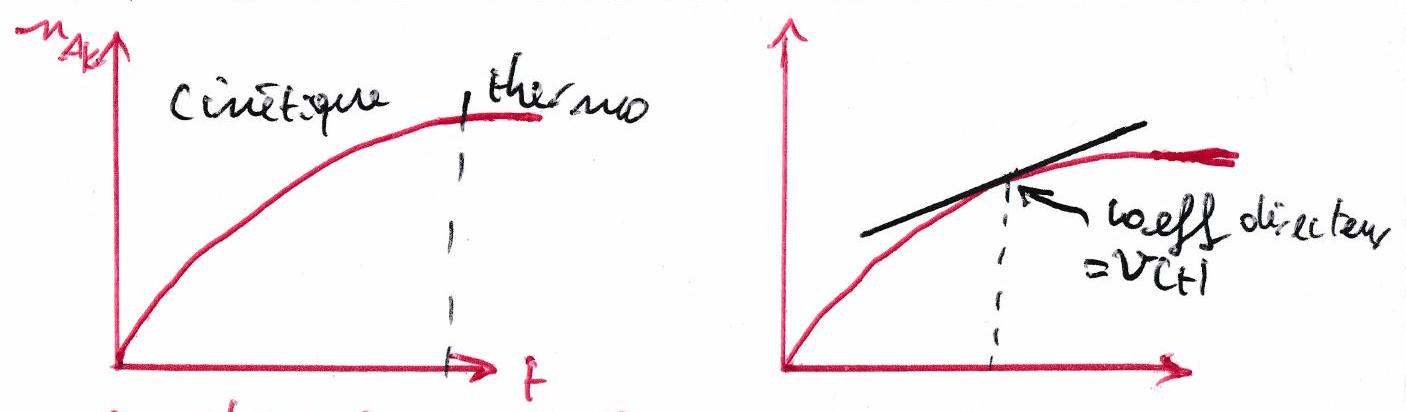
$R_{q}$ : dans la zone thermo : $v(t) = 0$ $\Rightarrow$ pas de variation de composition à l’échelle macroscopique.

5 Détermination expérimentale de l’ordre d’une réaction¶

5.1 Loi de vitesse en $v = k[A]^{n}$ ¶

Objectif : trouver la valeur de l’ordre partiel (donc global ici) $n$ . On relève expérimentalement les couples ( $[A] ; t$ ).

5.1.1 Méthode différentielle¶

On suppose que la réaction suit une loi de vitesse $v = k[A]^{n}$

\Rightarrow \ln(v) = \ln(k) + n \ln([A])

(4)

Ceci est de la forme $y = b + ax$ .

On dispose généralement de couples de valeurs ( $[A]; v(t)$ ). $\Rightarrow$ On trace $\ln(v) = f(\ln[A])$ .

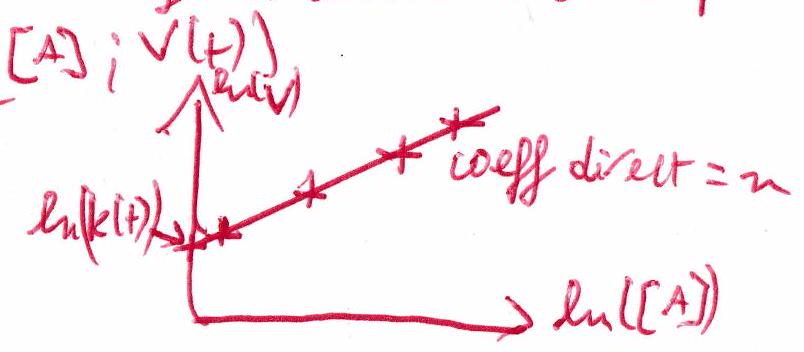
Comment valider un modèle linéaire ?¶

Visualiser (donc tracer !) la courbe issue de l’hypothèse d’ordre faite au préalable. Puis vérifier :

Si les points sont alignés, l’hypothèse de loi de vitesse est validée.
L’ordre est donné par le coefficient directeur.
$\ln k(T)$ est donné par l’ordonnée à l’origine.

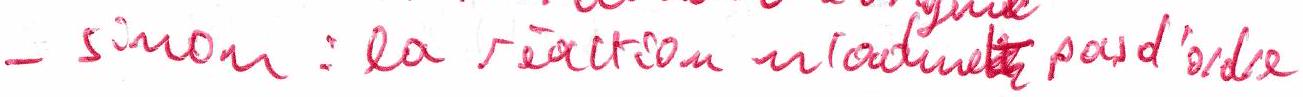
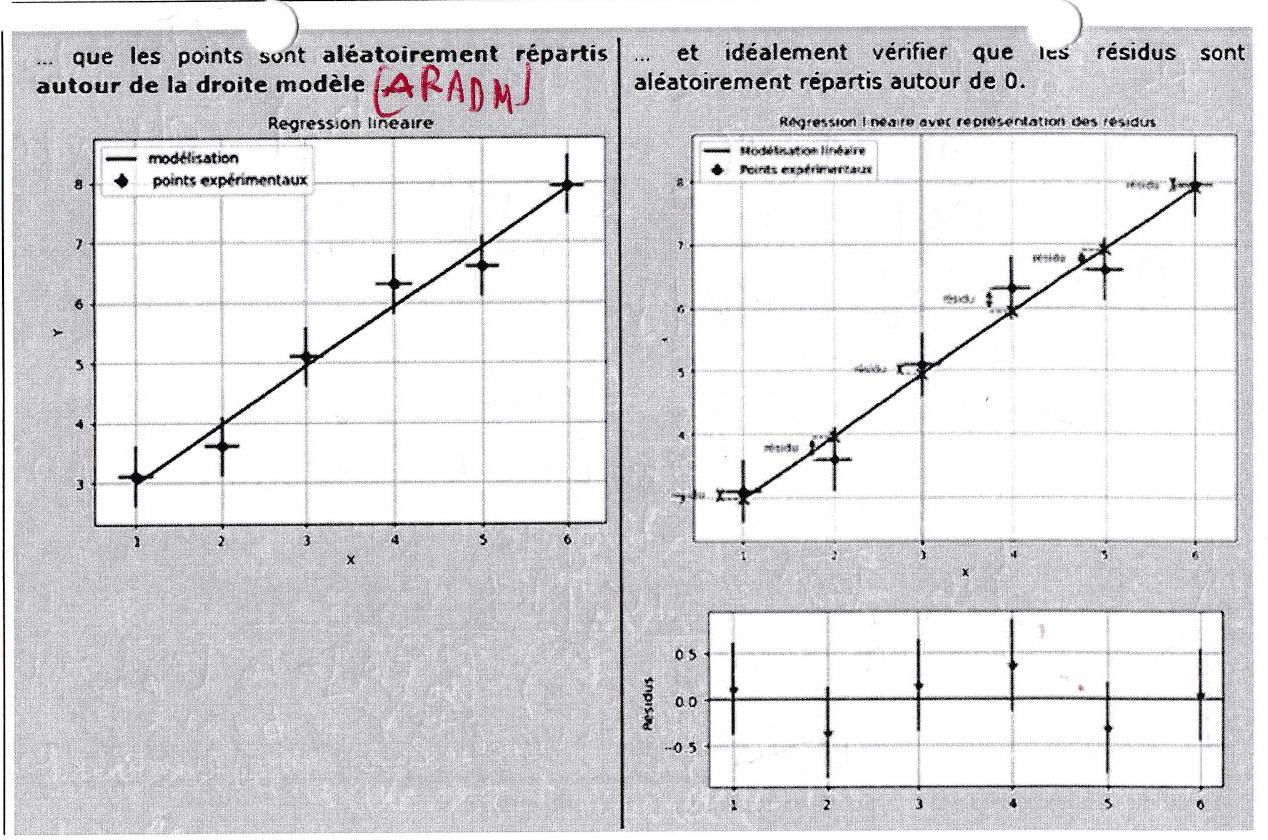
cf. les documents sur ELEA : « Régression linéaire » et « kit de survie de Python en TP de Chimie ».

En particulier : Méthode de la vitesse initiale¶

Utiliser la méthode différentielle ?
Quand ? Quand on dispose des valeurs de vitesse de réaction à un même instant (généralement initial) pour différentes concentrations en réactifs.
Comment ? On linéarise la loi de vitesse à l’instant considéré en prenant le logarithme.

Avez-vous tout compris ? - $n^{\circ} 5$ ¶

5.1.2 Méthode intégrale (et méthode du temps de demi-réaction)¶

On dispose de points $(t ; [A](t))$ ou pression, ou absorbance, ou $\sigma(t)\dots$ On suppose que la réaction admet une loi de vitesse $v = k[A]^n$ en donnant une valeur a priori au $n = 0, 1, 2 \dots$

$\Rightarrow$ À partir des résultats expérimentaux liant différents $t_{1/2}$ à différentes concentrations initiales $[A]_0$ , on peut obtenir l’ordre de la réaction étudiée.

Avez-vous tout compris ? - $n^{\circ} 8$ ¶

Utiliser la méthode du temps de demi-réaction (ou de 1/4 de réaction, ou de 1/8…) ?
Quand ? Quand on dispose des $t_{1/2}$ pour différentes expériences menées avec des concentrations initiales différentes (soit un ensemble de points $(t_{1/2} ; [A]_0)$ ).
Comment ? On retrouve, avec la méthode intégrale, la relation liant $t_{1/2}$ à $[A]_0$ . Puis on vérifie (par linéarisation s’il y a plus de 2 couples de valeurs) que les points expérimentaux vérifient la relation obtenue.

Récapitulatif de la méthode intégrale et de la méthode de $t_{1/2}$ ¶

Hypothèse : ordre supposé	0	1	2
Loi de vitesse supposée	$v = k$	$v = k[A]$	$v = k[A]^2$
Comme par ailleurs $v = -\frac{1}{	v_A	} \frac{d[A]}{dt}$ : intégration	$A = [A]_0 -
Droite modèle (à confronter aux points exp.)	$[A] = f(t)$	$\ln[A] = f(t)$	$\frac{1}{[A]} = f(t)$
Coefficient directeur	$-	v_A	k$
$t_{1/2}$	$\frac{[A]_0}{2	v_A	k}$

5.2 Loi de vitesse en $v = k[A]^{\alpha}[B]^{\beta}$ ¶

5.2.1 Méthode d’isolement d’Ostwald ou de la dégénérescence d’ordre¶

Utiliser la méthode de la dégénérescence d’ordre
Quand ? Quand un des réactifs (au moins) est introduit en quantité largement minoritaire par rapport aux autres (typiquement au moins un facteur 10).
Comment ? On néglige, dans la loi de vitesse, la variation de concentration du (des) réactif(s) introduit(s) en large excès, qui est donc supposée constante et intégrée avec son ordre partiel à une constante de vitesse apparente $k_{app}$ . $\Rightarrow$ On se ramène ainsi au cas de l’étude d’une loi de vitesse à un réactif (méthode différentielle, intégrale...).
$v = k_{app}[A]^{\alpha}$
(5)
Avec $k_{app} = k[B]_0^{\beta}$

Avez-vous tout compris ? - $n^{\circ} 9$ ¶

5.2.2 Cas particulier : réactifs en proportions stœchiométriques¶

Rappel : Les « conditions stœchiométriques » signifient que les réactifs sont introduits tels que :

\frac{n_{A}^{\text{initial}}}{|v_A|} = \frac{n_{B}^{\text{initial}}}{|v_B|} = n_0

(6)

| (en mol.L⁻¹) | $\xi$ | $|v_A|A$ | + | $|v_B|B$ | = | Produits | | :--- | :--- | :--- | :--- | :--- | :--- | :--- | | $t = 0$ | 0 | $[A]_0 = |v_A|C_0$ | | $[B]_0 = |v_B|C_0$ | | 0 | | $t$ | $\xi(t)$ | $[A](t) = |v_A|(C_0 - x(t))$ | | $[B](t) = |v_B|(C_0 - x(t))$ | | ... |

Utiliser la méthode des conditions stoechiométriques
Quand ? Quand on travaille avec des réactifs en proportions stoechiométriques.
Comment ? On exprime les concentrations des réactifs en fonction d’un seul d’entre eux grâce à la relation de stoechiométrie. On se ramène ainsi au cas de l’étude d’une loi de vitesse à un réactif (méthode différentielle, intégrale...).

6 Introduction à la catalyse¶

6.1 Définition d’un catalyseur¶

Catalyseur : substance qui :
accélère la réaction,
sans apparaître dans son bilan (car est régénéré en fin de réaction),
sans modifier l’état final prévu par la thermodynamique.

Un catalyseur ne peut pas rendre favorable une réaction défavorable thermodynamiquement (il ne modifie ni le $Q_r$ ni le $K^0$ ). $\Rightarrow$ Une petite quantité de catalyseur est donc souvent suffisante.

Autocatalyse : lorsqu’un produit de réaction est lui-même un catalyseur de la réaction.

6.2 Effet catalytique sur le profil énergétique¶

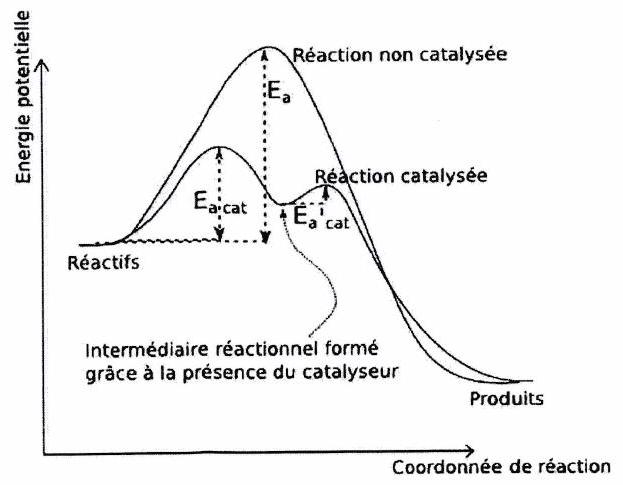
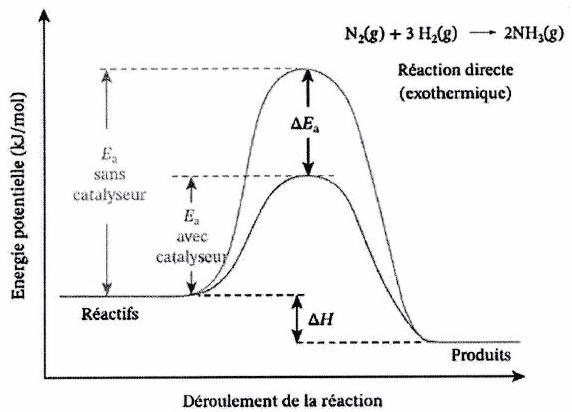
6.3 Différents types de catalyse¶

6.3.1 Catalyse homogène¶

Le catalyseur appartient à la même phase que les réactifs et les produits. Il intervient par sa concentration. Bien que le catalyseur soit régénéré, l’utilisation d’une plus grande quantité a un meilleur effet catalytique, car la réaction admet généralement un ordre par rapport au catalyseur.

6.3.2 Catalyse hétérogène¶

Le catalyseur (souvent solide) n’est pas dans la même phase que les réactifs (liquides ou gazeux) : il intervient seulement à l’interface réactionnelle. L’activité du catalyseur est désormais liée à sa surface : d’où le choix pour un catalyseur solide de poudre très finement divisée.

6.3.3 Catalyse enzymatique¶

Enzyme : protéine (polymère d’acides aminés) accélérant une réaction biologique de manière très sélective. Cette partie sera étudiée dans le chapitre 10 sur les mécanismes réactionnels.

6.4 Intérêt des catalyseurs dans le domaine industriel et le milieu biologique¶

Dépollution des gaz d’échappements.
Le raffinage pétrolier.
Le traitement des eaux.
La production de dihydrogène.
La production de biocarburants.
Le recyclage chimique des matières plastiques.
les réactions de polymérisation
Intérêts de l’utilisation des catalyseurs dans l’industrie chimique :
utilisation plus faible de réactifs et création de moins de déchets : c’est moins coûteux en matières premières et plus écologique.
les réactions sont plus rapides et permettent de faire des économies d’énergie.

6.3 Différents types de catalyse¶

6.3.1 Catalyse homogène¶

6.3.2 Catalyse hétérogène¶

6.3.3 Catalyse enzymatique¶

7 CONNAISSANCES ET COMPÉTENCES EXIGIBLES¶

Notions et contenus	Capacités exigibles
Cinétique en réacteur fermé de composition uniforme Vitesses volumiques de consommation d’un réactif et de formation d’un produit. Vitesse de réaction pour une transformation modélisée par une réaction chimique unique (supposée sans accumulation d’intermédiaires).	Relier la vitesse de réaction, dans les cas où elle est définie, à la vitesse volumique de consommation d’un réactif ou de formation d’un produit.
Lois de vitesse : réactions sans ordre, réactions avec ordre simple ( $0, 1, 2$ ), ordre global, ordre apparent. Temps de demi-vie d’un réactif, temps de demi-réaction.	Établir une loi de vitesse à partir du suivi temporel d’une grandeur physique. Exprimer, pour une transformation modélisée par une seule réaction chimique, la loi de vitesse si la réaction chimique admet un ordre et déterminer la valeur de la constante de vitesse à une température donnée. Déterminer la vitesse de réaction à différentes dates en utilisant une méthode numérique ou graphique. Déterminer un ordre de réaction à l’aide de la méthode différentielle ou à l’aide des temps de demi-réaction. Confirmer la valeur d’un ordre par la méthode intégrale, en se limitant strictement à une décomposition d’ordre 0, 1 ou 2 d’un unique réactif, ou se ramenant à un tel cas par dégénérescence de l’ordre ou conditions initiales stœchiométriques. Capacité numérique : à l’aide d’un langage de programmation ou d’un logiciel dédié, et à partir de données expérimentales, tracer l’évolution temporelle d’une concentration, d’une vitesse volumique de formation ou de consommation, d’une vitesse de réaction et tester une loi de vitesse donnée.
Loi empirique d’Arrhenius ; énergie d’activation.	Déterminer l’énergie d’activation d’une réaction chimique. Déterminer la valeur de l’énergie d’activation d’une réaction chimique à partir de valeurs de la constante cinétique à différentes températures.
Facteurs concentration et $T$ en stratégie de synthèse et d’analyse : dilution, chauffage, reflux, trempe.	Reconnaître, dans un protocole, des opérations visant à augmenter ou à diminuer une vitesse de réaction.
Suivi cinétique de transformations chimiques Suivi de l’évolution temporelle d’une grandeur physique. Limitation de l’évolution temporelle (trempe) d’un système par dilution, transformation chimique ou refroidissement. Régulation de la température.	Choisir une méthode de suivi prenant en compte la facilité de mise en œuvre, les propriétés des espèces étudiées, la durée de la transformation estimée ou fournie. Exploiter les résultats d’un suivi temporel de concentration pour déterminer les caractéristiques cinétiques d’une réaction. Proposer et mettre en œuvre des conditions expérimentales permettant la simplification de la loi de vitesse. Déterminer la valeur d’une énergie d’activation.

1 Vitesses d’une réaction chimique¶

1.1 Vitesse volumique de réaction (ou vitesse de la réaction)¶

1.2 Vitesses volumiques relatives à chaque espèce (apparition/disparition)¶

Avez-vous tout compris ? - n∘1n^{\circ} 1n∘1¶

1.3 Identification graphique de la vitesse de réaction¶

5 Détermination expérimentale de l’ordre d’une réaction¶

5.1 Loi de vitesse en v=k[A]nv = k[A]^{n}v=k[A]n¶

5.1.1 Méthode différentielle¶

Comment valider un modèle linéaire ?¶

En particulier : Méthode de la vitesse initiale¶

Avez-vous tout compris ? - n∘5n^{\circ} 5n∘5¶

5.1.2 Méthode intégrale (et méthode du temps de demi-réaction)¶

Avez-vous tout compris ? - n∘8n^{\circ} 8n∘8¶

Récapitulatif de la méthode intégrale et de la méthode de t1/2t_{1/2}t1/2​¶

5.2 Loi de vitesse en v=k[A]α[B]βv = k[A]^{\alpha}[B]^{\beta}v=k[A]α[B]β¶

5.2.1 Méthode d’isolement d’Ostwald ou de la dégénérescence d’ordre¶

Avez-vous tout compris ? - n∘9n^{\circ} 9n∘9¶

5.2.2 Cas particulier : réactifs en proportions stœchiométriques¶

6 Introduction à la catalyse¶

6.1 Définition d’un catalyseur¶

6.2 Effet catalytique sur le profil énergétique¶

6.3 Différents types de catalyse¶

6.3.1 Catalyse homogène¶

6.3.2 Catalyse hétérogène¶

6.3.3 Catalyse enzymatique¶

6.4 Intérêt des catalyseurs dans le domaine industriel et le milieu biologique¶

6.3 Différents types de catalyse¶

6.3.1 Catalyse homogène¶

6.3.2 Catalyse hétérogène¶

6.3.3 Catalyse enzymatique¶

7 CONNAISSANCES ET COMPÉTENCES EXIGIBLES¶

6.4 Intérêt des catalyseurs dans le domaine industriel et le milieu biologique¶

8 Les « Avez-vous tout compris ? »¶

Table des matières¶

1 Vitesses d’une réaction chimique¶

1.1 Vitesse volumique de réaction (ou vitesse de la réaction)¶

1.2 Vitesses volumiques relatives à chaque espèce (apparition / disparition)¶

1.3 Identification graphique de la vitesse de réaction¶

2 SUIVI EXPÉRIMENTAL D’UNE CINÉTIQUE DE RÉACTION¶

2.1 Méthodes chimiques¶

2.2 Méthodes physiques¶

3 ASPECT MICROSCOPIQUE D’UNE TRANSFORMATION CHIMIQUE¶

3.1 Profil énergétique d’une transformation¶

3.2 Mécanisme réactionnel¶

4 FACTEURS CINÉTIQUES¶

4.1 Influence des concentrations¶

4.1.1 Loi de vitesse - Ordre d’une réaction, ordre courant, ordre initial¶

4.1.2 Dégénérescence d’ordre¶

4.2 Influence de la température¶

5 DÉTERMINATION EXPÉRIMENTALE DE L’ORDRE D’UNE RÉACTION¶

5.1 Loi de vitesse en v=kAn\boldsymbol{v}=\boldsymbol{k} A^nv=kAn¶

5.1.1 Méthode différentielle¶

5.1.2 Méthode intégrale (et méthode du temps de demi-réaction)¶

5.2 Loi de vitesse en v=kAαBβ\boldsymbol{v}=\boldsymbol{k} A^\alpha B^\betav=kAαBβ¶

5.2.1 Méthode d’isolement d’Ostwald ou de la dégénérescence d’ordre¶

5.2.2 Cas particulier : réactifs en proportions stœchiométriques¶

6 INTRODUCTION À LA CATALYSE¶

6.1 Définition d’un catalyseur¶

6.2 Effet catalytique sur le profil énergétique¶

Avez-vous tout compris ? - $n^{\circ} 1$ ¶

5.1 Loi de vitesse en $v = k[A]^{n}$ ¶

Avez-vous tout compris ? - $n^{\circ} 5$ ¶

Avez-vous tout compris ? - $n^{\circ} 8$ ¶

Récapitulatif de la méthode intégrale et de la méthode de $t_{1/2}$ ¶

5.2 Loi de vitesse en $v = k[A]^{\alpha}[B]^{\beta}$ ¶

Avez-vous tout compris ? - $n^{\circ} 9$ ¶

5.1 Loi de vitesse en $\boldsymbol{v}=\boldsymbol{k} A^n$ ¶

5.2 Loi de vitesse en $\boldsymbol{v}=\boldsymbol{k} A^\alpha B^\beta$ ¶